2024年5月22日
人事のためのデータ分析講座 回帰分析:有効な影響指標を探る方法を学ぶ(セミナーレポート)
ビジネスリサーチラボは、2023年7月にセミナー「人事のためのデータ分析講座 ~回帰分析:有効な影響指標を探る方法を学ぶ~」を開催しました。
「従業員のエンゲージメントを高める要因は何か」「上司・仕事・組織の要因のうち、職務満足を最も高めるものはどれか」など、ある指標に影響する要因の影響力を分析する統計的な手法として「回帰分析」があります。
回帰分析を用いることで、サーベイで測定した様々な影響指標から、成果指標を高めるのにより有効な指標を見つけることができます。実務的な関心にも貢献度が大きい、この回帰分析について、ビジネスリサーチラボ フェローの能渡 真澄が解説しました。
※レポートはセミナーの内容を基に編集・再構成したものです。
回帰分析が関わる実務上の関心
本日のセミナーのテーマは、回帰分析です。回帰分析は、主に影響力の大きさを分析するもので、実務家の多くの方々が気になる「どうやったら成果指標を上げることができるのか?」という疑問の解決に役立つものです。
「成果指標」とは、サーベイ実施の目的・目標となる、組織や従業員の最終的な状態を表す指標を指します。
例えば、サーベイ実施において「職場の人間関係を良くしたい」という目標がある場合、「職場の人間関係の良さ」を表す指標が成果指標になります。この成果指標を上げるためには、まず何が影響を与えているのかを理解することが必要です。
職場の人間関係を良くしたい場合、様々な要因が影響すると考えられます。例えば「職場の雰囲気」や「仕事の仕組み」、あるいは「上司の態度」などです。これらの成果指標を高める要因となる指標を「影響指標」と呼びます。
この影響指標が、成果指標にどれくらい影響しているのかを把握できれば、サーベイの目的達成に近づく手がかりとなるでしょう。どの要因が成果に影響を与えるのかがわかれば、どういった対策をどの部分を改善すればいいのかが見えてきます。
影響指標が成果指標にどの程度影響しているか検証する際によく用いられるのは「組織サーベイ」です。これは、成果指標とその要因となる様々な影響指標について、主にアンケートを使ってデータ測定することです。そこで得られたデータを分析することで、影響指標と成果指標の関連を検証できます。
実際に、そういった関心を持って組織サーベイを実施し、データを測定した経験がある方も多いのではないでしょうか。
しかし、ここで多くの方が悩むのが、「このデータをどう分析すれば、成果指標を高める有効な影響指標が把握できるのかわからない」という点です。データがたくさん集まっても、そのデータを単純集計して眺めているだけでは、有効な影響指標はなかなか見えてきません。
まずここで役立つのが「相関分析」という方法です[1]。これは、目標と影響指標の間にどれだけ強い関連性があるかを数値で示してくれます。例えば、「職場の雰囲気が良い」と「人間関係が良い」の間に強い関連性が見られれば、雰囲気を良くすることが人間関係を良くするために有効であると考えられます。
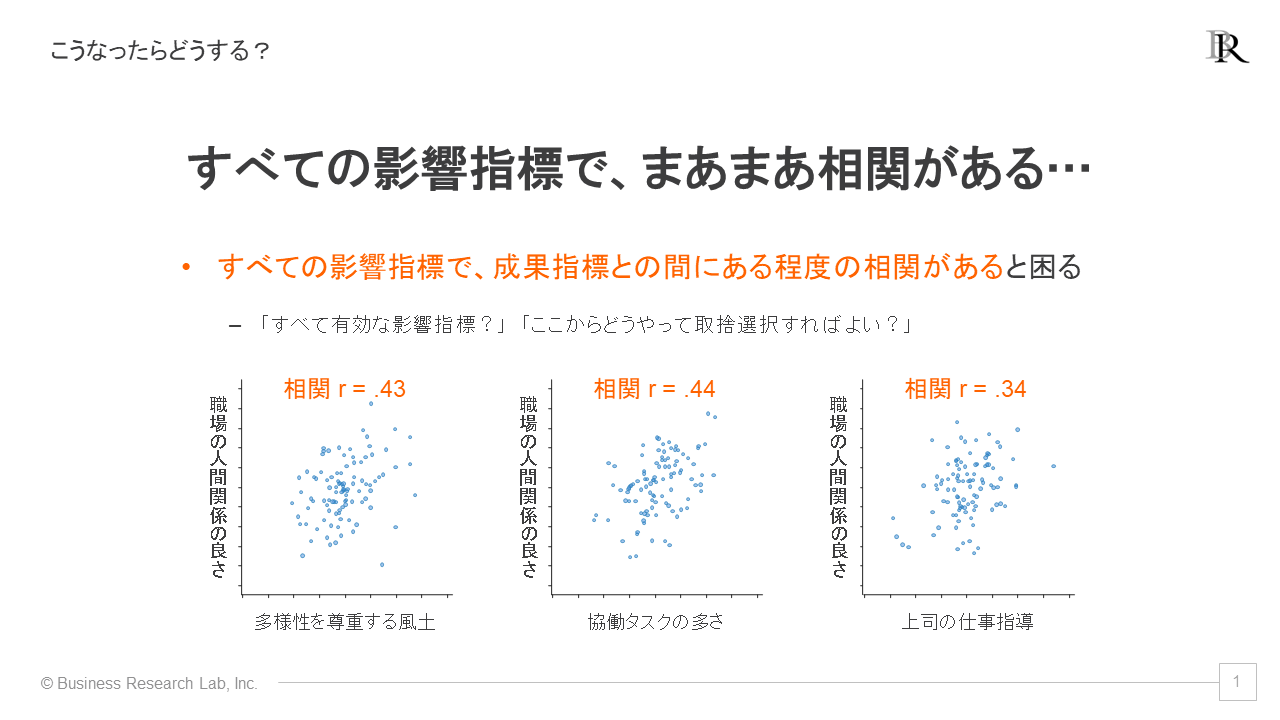
ただ、注意が必要なのは、すべての影響指標が目標と何らかの関連性を持っていた場合です。つまり、多くの要素が関連していると、どれを優先して手をつければいいのかがわからなくなってしまうこともあります。
先ほど話した「多様性を尊重する風土」「共同タスクの多さ」「上司の指導力」の三つの影響指標と、目標である「職場の人間関係の良さ」との間に同程度の相関係数がみられたとします。しかし、これだけだとどれを重視すれば良いのかがわかりません。
そんな時に役立つのが「回帰分析」という手法です。これは、複数の影響指標が成果指標にどれだけ影響を与えるのかを詳しく解析できます。要するに、どの要素が一番効果が高いのか、どれを優先すべきかがより明確にわかります。
記述統計としての回帰分析
では、回帰分析とは何かを端的に述べると、「成果指標に影響を与える影響指標はどれか」を検証する分析手法です。例えば、「多様性を尊重する風土(影響指標)が、職場の人間関係(成果指標)にどれだけ影響を与えるか」を数値で見ることができます。
ここで、データ分析の際に気をつけなければならない点があります。それは、手元にあるデータは「回答してほしい従業員全員から集めたデータ」ではなく、一部であることがほとんどだということです。この「従業員全員」を母集団と言います。
手元のデータはこの母集団から取った一部であり、母集団の特徴を100%正確に反映できているとはいえないため、注意が必要です。この考えに応じて、統計学では「実際に得られた手元のデータの特徴を調べる」ための記述統計と、「手元のデータから母集団の特徴を推測する」ための推測統計の2種類を使い分けます。
回帰分析も、記述統計と推測統計の枠組みがあります。本日のセミナーでは、アンケートデータを分析するイメージで話を進めていきつつ、記述統計としての回帰分析と、推測統計としての回帰分析を解説していきます。
なお、以降の解説では数式が出てきますが、それを覚える必要はありません。数式を見ながら、回帰分析がどのような考え方で行われるのか、そのイメージをつかんでいただければと思います。
影響力を調べる:「傾き」の算出
まず、回帰分析とは具体的に何を計算するのかを説明していきます。端的に言えば、回帰分析は散布図に描かれる回帰直線の傾きについて分析するものです。散布図とは、2指標の得点を横軸・縦軸にとり、各回答者のデータをひとつひとつ点でプロットしたものです。
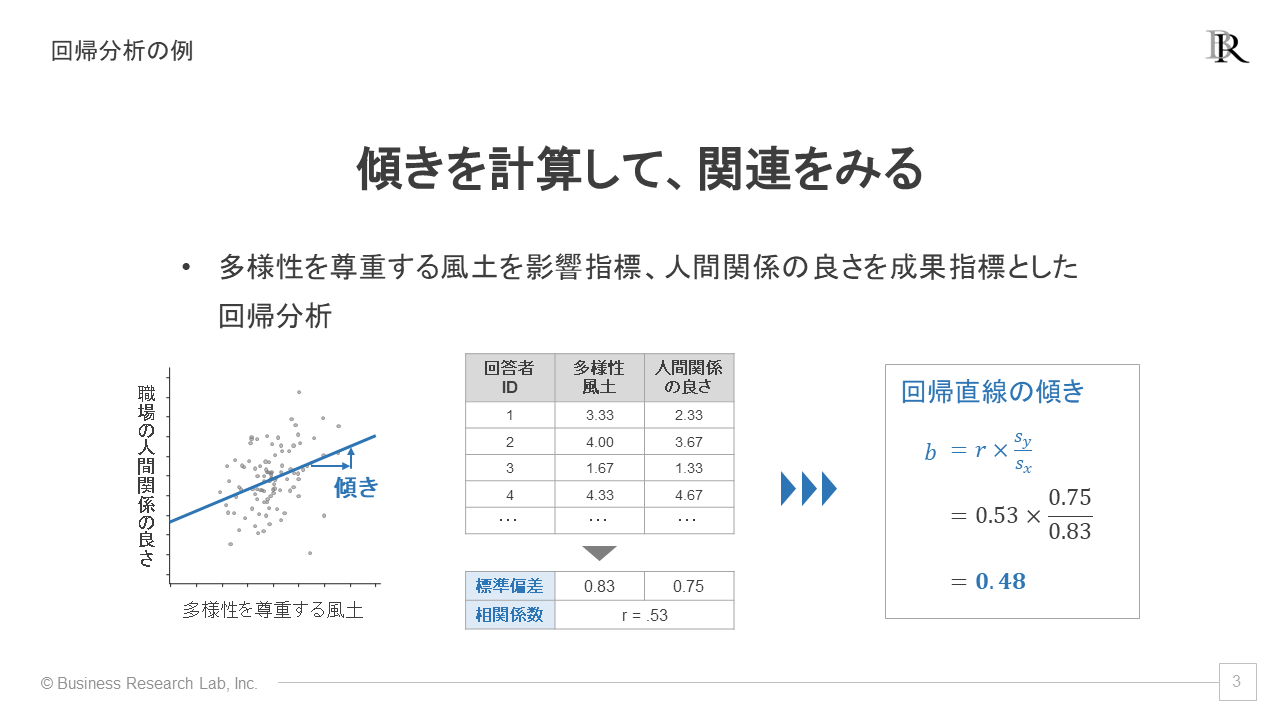
影響指標を横軸、成果指標を縦軸に取って散布図を描きます。この図の各点の傾向をうまく表す直線(これを回帰直線と呼びます)を引くイメージです。中学生のころにやった「グラフの上の2点を結んで直線を描け」という問題に似た考え方で、今回は点が複数あるのが特徴です[2]。
この回帰直線の傾きは回帰係数とも呼ばれ、とても重要です。傾きは、影響指標が1ポイント増えたら、成果指標の得点が何ポイント上がるのかを表します。つまり、傾きが大きいほど、影響指標が成果指標に大きな影響を与えていると解釈できます。
分析のイメージとして、仮想のデータを使った計算例を以下に示します。実は、回帰係数を算出すること自体は難しくありません。計算式は単純ですし、Excelの「SLOPE」関数を使っても、傾きを簡単に計算できます。
予測とのズレを調べる:「残差」の算出
回帰分析では、傾きの情報に加えて、回帰直線と回答データの「ズレ」に関する情報も使います。回帰直線は、散布図の各点をもとに、成果指標の得点の高さを影響指標の値を使って表現した直線です。しかし、散布図の各点、つまり実際の回答データと回帰直線にはいくらかずれがあります。
以下の散布図と回帰直線の間にあるオレンジの線が、回帰直線と各データのずれです。回帰直線と実際の回答データに生じるずれを、残差と言います。
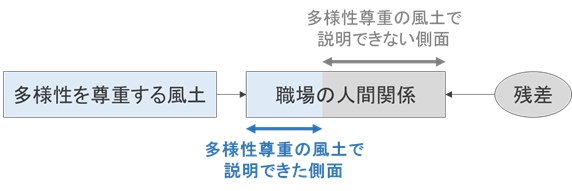
回帰分析で残差がなぜ重要かというと、影響指標では説明できない、成果指標の側面を表すというものだからです。
職場の実態を考えたとき、職場の人間関係は、多様性を尊重する風土の有無だけでなく、他の様々な要因で変わってくるでしょう。言い換えれば、多様性を尊重する風土の有無だけでは説明できない、職場の人間関係の側面があると考えられます。
つまり、「影響指標で説明できない成果指標の側面が存在する」というわけですが、回帰分析ではこれを残差として扱えるということです。
予測できる度合いを調べる:「決定係数」の算出
この残差を扱えることで、有効な情報が得られます。それは、「影響指標が成果指標をどの程度説明できるのか」を逆算できることです。
影響指標が成果指標をどの程度説明するか、その程度を数値化したものは「決定係数」と呼ばれます。例えば以下の図のように、「R2=.42」という具合に表記され、これは「成果指標が影響指標によって説明される側面が全体の42%である」という結果を示します。
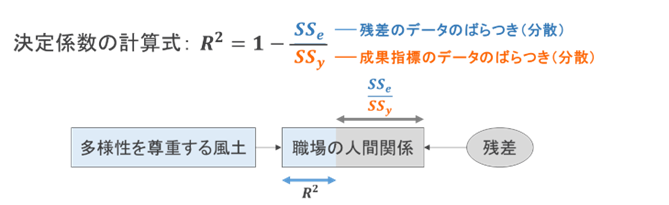
この決定係数が、残差を利用することで算出できるのです。大まかにいうと、「影響指標によって説明されない側面の割合」から逆算することで、決定係数を計算することができます。具体的には、以下のような数式で表されます。
計算式に含まれる分数の式は、影響指標で説明されない成果指標の側面がどの程度あるのかという割合を表すものです(上記の下図、灰色の部分)。その割合を1、つまり100%から引き算することで、成果指標が説明された割合が算出されます。
このように、残差の情報を生かすことで、成果指標がどのくらい説明されたか検証ができるのです。
推測統計としての回帰分析
結論「統計的に有意」かの検討
続いて、推測統計について説明します。ここまでは実際に得られた手元のデータの分析でしたが、ここからは、手元のデータから推測される回答者候補全体の特徴を検証するということです。
他の分析と同様に、回帰分析の推測統計も「統計的に有意か」を確認する流れになっています。統計的に有意とは、分析結果が偶然やランダムな要因によって説明されないということです。回帰分析では、「手元の分析結果で示された影響指標が成果指標に及ぼす影響は、偶然示されたものでなく、確かなものといえそうだ」ということを表します。
統計的に有意か否かを検証するには帰無仮説検定を行います。その検証プロセスは分析ツールが担ってくれますので、今回はその検証結果の判断ポイントであるp値を確認する流れについてだけ、かいつまんで説明します[3]。
p値を見れば、「分析で取り上げた影響指標たちによって、成果指標は説明されるのか」や、「影響指標それぞれにおいて、影響力があるといえるのか」が把握できます。
なお「統計的に有意である」という結果は、影響力が大きいことのエビデンスではないことには注意が必要です。「統計的に有意」が示すのは、あくまで「影響があると統計的にいえる」ということだけで、これだけではその影響力の大きさに言及できません。
したがって、各影響指標の影響力が大きいかどうかは、p値以外の数値を確認して結果を解釈するのが大事になります。
母集団における決定係数と傾きの検討
回帰分析における帰無仮説検定では、決定係数と傾きについて母集団の状態がどうなっているのかを検証します。具体的な例で説明します。
例えば、会社で「多様性を尊重する風土」を影響指標、「職場の人間関係」を成果指標として、その影響を調べたとします。このとき、分析ツールを使ってp値を計算すると、以下のような結果が示されます。
この結果では、決定係数と傾きのいずれもp値が.000と.05を下回っています。経営学や心理学の慣行では、p値が.05(5%)を下回っていると統計的に有意だと判断します。
そのため、この結果から決定係数と傾きはどちらも統計的に有意であり、「多様性を尊重する風土によって職場の人間関係は説明される側面があり、その影響はあるといえそうだ」のだと解釈します。
このように、回帰分析の帰無仮説検定では、算出されるp値を見ることで「成果指標を影響指標によって説明されたか」という決定係数と、「影響指標が成果指標に及ぼす影響の大きさ」である傾きが、統計的に有意であるか検証することができます。
続けて、「統計的に有意」という結果を得た後は、成果指標はどの程度説明されたのか、影響指標がどれくらいの影響力を持っているのかを、具体的な数値で評価します。
決定係数については、研究者Cohenが以下のような基準を提案しています。
- R2 ≧ .13:中程度の説明力
- R2 ≧ .26:大きな説明力
今回の仮想データで得られたR2の値は.28です。これは、“説明力が大きい“という基準の.26を超えています。つまり、職場の人間関係はこの分析で取り上げた影響指標によって、十分に説明されていると考えることができます。
次に、傾きのあたり影響力の値を確認するのですが、ここは難しいところです。なぜなら、傾きの大きさには基準値がありません。つまり、成果指標はいくら高まると大きいと言えるかは、成果指標に応じて判断する必要があります。例でいえば、職場の人間関係が何ポイント高まると高い効果といえるかは、サーベイ実施者の判断になるということです。
重回帰分析とは
基本方針は影響力の比較
ここまでは、影響指標がひとつだけの回帰分析について説明してきましたが、これは単回帰分析と呼ばれます。それに対して、複数の影響指標を取り上げて行う回帰分析があり、それを重回帰分析と言います。重回帰分析は、実務上の関心によりフィットした検証が可能です。
重回帰分析の基本方針は、「複数の影響指標について、より影響力の強く有効な指標はどれかを探る」ことです。改めて、仮想の例を示します。この例では、良好な人間関係を築くために影響を与えると考えた三つの影響指標を評価しています。
ここでの目的は、「職場の人間関係を高めるうえで、多様性を尊重する風土、協働タスクの多さ、上司の仕事指導のうち、どれが最も効果的なのか」を見つけ出すことです。このような複数の要素を一度に評価するときに重回帰分析が使えます。
重回帰分析を行うと、二つのことが示されます。まず、取り上げた影響指標全体で成果指標をどの程度説明できるのかを、決定係数として評価できます。次に、影響指標それぞれが成果指標にどの程度影響するのかを、傾きによって比較できます。これにより、最も影響力の高い有効な影響指標を特定することができるのです。
「標準偏回帰係数」を算出する
重回帰分析について、具体的な計算内容を見ていきます。初めに、重回帰分析における決定係数について説明します。記述統計については、最初の単回帰分析と同様、残差から逆算ができます。
重回帰分析では、複数の影響指標を組み合わせて一つの回帰直線の式を作ります。この数式について、単回帰分析と同様に実際のデータとのズレを計算し、残差の情報を得ることができます。その残差を使って、決定係数を算出できるわけです。
次に、重回帰分析における傾きについて説明します。重回帰分析では、複数の影響指標を使うので、数式にはそれぞれの影響指標の傾きが含まれます。つまり、影響指標が増えるほど、傾きも増えることになります。
ただし、ここで一つ問題があります。それは、重回帰分析で得られる傾きは、そのままでは大きさを比べられないことです。理由は、影響指標に応じて、単位が異なるためです。
例えば、「10cmと20gはどちらが大きいか」と尋ねられたら、「比較できない」というのが正解です。傾きは影響指標ごとに単位が違うものとして算出されるので、そのままでは傾きの大きさを比べられないのです。
では、どうするか、その手続きを説明します。具体的には、傾きを「標準化偏回帰係数」と呼ばれるものに修正していきます。その特徴は、単位が違う問題を解決していることです。手続きとしては、「標準化」という統計的な処理を内部で行っています[4]。
標準化をすると、単位の影響を取り除くと同時に、値が-1~+1に収まるように得点を変換します。これによって、複数の影響指標の傾きを比較できるようになるのです。具体的には、標準化偏回帰係数の絶対値が大きい影響指標は、より大きな影響力を持っていると見なせます。
ちなみに、標準化偏回帰係数がプラスの値ならば「影響指標の得点が高いと、成果指標の得点も高い」影響、マイナスの値ならば「影響指標の得点が高いと、成果指標の得点は低い影響があることを意味します。
標準化偏回帰係数の特徴の二つ目は、それぞれの影響指標が持つ独自な影響力を「統制」によってうまく検証できることです[5]。これによって、影響指標に混ざり込んでいる他指標の要素をうまく除去するといったことができます。
統制が取り上げる問題の具体例を示します。例えば、「この会社で長く働きたい」と感じる程度である「定着意欲」を成果指標として、仕事に満足している程度である「仕事満足」と、会社や組織に愛着を感じている程度である「組織への愛着」を影響指標として取り上げ、どちらがより影響しているのかを調査するとします。
このとき、「仕事に満足している」という回答には、注意が必要です。なぜなら、「仕事自体が楽しくて満足している」人もいれば、「会社が好きで仕事にも満足感が生まれている」人がいることが予測されるからです。
同様に「この会社が好き」という回答も、単純に「会社が好きである」だけではなく、「楽しめる仕事ができる、この会社が好き」という理由でそのように回答する場合も考えられます。
これらの例から、仕事満足の回答には組織への愛着による側面が混入しており、また、組織への愛着の回答にも仕事満足による側面が混入していると考えられます。要するに、測定されたデータには、実は複数の要因が混ざりあっている可能性が高いのです。これは、データ測定が常にはらんでいる問題と言えます。
このような問題に対処するために、重回帰分析では基本的に「統制」の処理が行われます。以下に、そのイメージ図を示します。
仕事満足を見ると、図の左にある元のデータは、仕事満足による側面(青色)に加えて、組織への愛着(橙色)の側面も含んだものになっています。重回帰分析では、仕事満足が定着意欲に及ぼす影響を見る際、統制によって、仕事満足から組織への愛着による側面を除いた仕事満足による側面(青色)のみで定着意欲への影響力を検証されます。
組織への愛着が定着意欲に及ぼす影響を見る際も同様に、組織への愛着に混ざりこんでいる仕事満足の側面を除いて、組織への愛着の側面(橙色)のみで定着意欲への影響力が検証されます。
つまり、各影響指標が互いに混入している側面を分析で取り除き、各影響指標に独自の側面を抽出するのが、統制の役割です。これにより、各影響指標が成果指標に及ぼす影響を、より正確に検証できるというのが特徴になります。
ただし、標準化偏回帰係数の難点もあります。それは、この係数の増減に対して、影響指標と成果指標の得点の具体的な対応関係がわからない点です。
単回帰分析では、回帰係数にあたる傾きは「影響指標が1ポイント上がったときに成果指標が何ポイント分上がるか」という解釈しやすい指標でした。しかし、標準化偏回帰係数では、標準化と統制という処理が入るため、得点の意味合いが変わり、単純な解釈ができなくなるのです。
従って、標準化偏回帰係数はあくまでも、ある影響指標の影響力が他の影響指標と比べてどれくらい大きいか、という相対比較に使うものになります。「各影響指標の影響力は、どれだけ大きいのか」という絶対評価は難しいという点には注意してください。
重回帰分析における帰無仮説検定
続けて、重回帰分析における推測統計について解説していきます。重回帰分析でも、単回帰分析と同様に、決定係数と標準化偏回帰係数について検証します。これらに対して帰無仮説検定を行い判断を下すプロセスです。
実践例として、先ほどの取り上げた「多様性を尊重する風土、協働タスクの多さ、上司の仕事指導のうち、職場の人間関係に強く影響するのはどれか」を分析した例を紹介していきます。
重回帰分析も、分析ツールに三つの影響指標と成果指標を投入して分析を実行すると、このような分析結果が示されます。
分析を実行すると、手元のデータに関する記述統計として、決定係数や標準化偏回帰係数、そして、それぞれのp値が得られます。決定係数のp値と数値の解釈は単回帰分析と同様なので、ここでは特に、標準化偏回帰係数の解釈について述べていきます。
上記の仮想データでは、標準化偏回帰係数のp値は全て.05を下回っており、統計的に有意です。つまり、「母集団では、すべての影響指標について成果指標への影響があるといえそうだ」と判断します。
さらに、三つの影響指標の標準化偏回帰係数を見ると、「協働タスクの多さ」の値が一番大きい結果です。また、比較して見ると、「多様性を尊重する風土」も同等に標準化偏回帰係数が大きく、「上司の仕事指導」はやや小さいことがわかります。
この結果から、「職場の人間関係への影響力が強いのは協働タスクの多さがであり、多様性を尊重する風土は同等の影響力、上司の仕事指導の影響力は一歩劣る」と解釈できるのです。
こうした結果が得られたら、例えば、職場の人間関係の向上に向けて、協働タスクの増強や多様性を尊重する風土の醸成の対策をしようと考えられるでしょう。一方、上司の仕事指導は影響力が弱めなため、対策の優先度は低めで良いと考えることもできます。
このように重回帰分析を使えば、ある成果指標に対してより有効な影響指標を分析で見出すことができるようになります。
回帰分析の注意点
最後に、回帰分析の注意点を三つ取り上げます。回帰分析は非常に有用な分析ですが、分析で取り上げる指標や結果の解釈に注意が必要なポイントがあります。
順序データとカテゴリカルデータは使用できない
まず一つ目の注意点は、「順序データとカテゴリーデータは使えない」という制約です。具体的にどのようなデータなのかを、それが使えるかと併せて、以下の表にまとめました。
このように、回帰分析では使えない種類のデータが存在します。これから回帰分析に挑戦してみようとお考えの方は、このデータの種類についても考えた上で、サーベイで測定する内容を決めていただくのがよいでしょう[6]。
似すぎた影響指標は避けるべき
次の注意点は、「影響指標は似すぎているものを選んではいけない」ことです。これは、影響指標間の相関が強い場合、回帰分析の精度が下がるという重回帰分析の問題があるためです。この問題を多重共線性と呼びます。
例えば、仕事の成果を高める要因を探るべく、上司満足度と上司への信頼を影響指標として取り上げて、どちらがより仕事の成果に影響するか検証したとします。その際、上司満足度と上司への信頼の相関係数が r = .85 と非常に強かったとします。
このような、影響指標間の相関が強いものが含まれた状態で重回帰分析をすると、標準化偏回帰係数の計算精度が下がります[7]。そのため、算出された標準化偏回帰係数の大きさ、つまり影響力の大きさの評価指標を信用できない問題が生じます。
この多重共線性の問題を避けるべく、影響指標を取り上げる際は、互いに似ておらず相関が弱そうな指標を影響指標として取り上げることをおすすめします。
因果関係は保証されない
三つ目の注意点は、ここまで影響力と述べてきていますが、重回帰分析は因果関係を保証するわけではない、ということです。確かに回帰分析は、影響指標と成果指標に因果関係を想定して分析しますが、分析手続きだけでは、因果関係を保証することはできません。
因果関係を示すには、それを満たすサーベイ設計が必要です。裏を返せば、妥当なサーベイ設計がなされていない場合には、因果関係があると強く主張しないほうがよいでしょう[8]。
Q&A
Q:重回帰分析を行うデータが正規分布しているかを検証する必要はあるか
本日の解説は概要解説なので割愛しましたが、厳密な回帰分析の手続きとしては、正確な結果を得るために、「正規分布しているかどうか」の確認はすべきです。
なお、正規分布か確認するのは、解説でも出てきた「残差」についてです。重回帰分析の数式では残差が式に含まれていますが、実は残差には正規分布が仮定されています。そのため、分析で得られた残差のデータが正規分布でないと、分析の仮定が満たされておらず分析結果の正確性が怪しい可能性が残ってしまいます。
Q:多重共線性に配慮して指標間の関連が遠いものを選ぶのにどのような方法があるか
まず、直感的に考えて「これは強く関連していそうで、例外もほぼ思いつかない」と思うような指標を選ばない方法が考えられます。
例えば、先ほど取り上げた「上司への満足度」と「上司への信頼」のような指標は、「上司への満足度が高い人は、上司への信頼も高いであろう」ことは普通に考えられ、加えて、「上司への満足度は高いが信頼は低い」という例外も、ほとんどなさそうです。
このように、直感的に考えて「まず相関がありそうだ」ということに加え、「その相関関係において例外はなさそうだ」ということも強く確信できるような指標は、選ばないようにするのがベターでしょう。
加えて、可能ならば、学術研究を参照するのも有効です。測定したい事柄について学術研究を調べてみて、研究ではそれらの相関がどうなっているか確認するのが良いでしょう。最近はAIによる研究検索機能も発展していますし、情報を手に入れやすくなっているかもしれません。
最後のポイントは、影響指標のカテゴリーを多様にすることです。仕事について、上司について、会社について、同僚について、従業員自身についてなど、異なるカテゴリーから影響指標を選ぶようにすると、相関が強くなりにくいです。
この方法は、様々な角度から成果指標への影響を検討するうえでも有効なアプローチであり、ぜひ生かしていただきたいと思います。
Q:影響指標がどのくらい似ていてはいけないのか、具体的な判断基準はあるか
心理学の分析でたびたび述べられる経験則ですが、相関関係がr = .70以上と非常に強いと、注意が必要です[9]。
もし調査で選んだ要素が似ていると、その調査が本当に有用かどうか、深く考える必要があります。要は、選んだ要素がほぼ同じことを測っているなら、一つだけに絞るか、それらを統合するなどして調査を効率的にすべきです。
脚注
[1] このセミナーの内容は、弊社コラム「人事のためのデータ分析講座 相関分析 ~二つの指標の関連を検証する~(セミナーレポート)」で公開されています。相関分析は関連性を検証する統計解析全般の土台となる基本的手法なため、データ分析に関心のある方はぜひこちらも合わせてお読みください。
[2] 回帰分析では、2点を結ぶ直線でなく、全回答データの点に対して直線を引くわけですが、そこでは「最小二乗法」と呼ばれる計算手法が用いられます。これは、後述する残差について、「全回答データにおける残差を二乗した値の合計が、最も小さくなる」よう計算する手法で、回帰直線の傾きや解説を割愛した切片の数式は、この手法で得られる式です。
[3] 統計的に有意であることを確認する手続きについて、詳細は以下のコラムをご参考ください;
人事のためのデータ分析講座「統計的に有意」を学ぶ(セミナーレポート)
[4] 標準化の手続きの詳細は、当社の以下のコラムで紹介していますので、適宜参照ください。
人事のためのデータ分析講座 相関分析 ~二つの指標の関連を検証する~(セミナーレポート)
[5] 統制の手続きの詳細は、当社のコラムでも紹介しています。適宜ご参照ください。
[6] データの種類についての詳細な説明は、当社の以下のコラムで詳しく解説しています。適宜参照ください。
[7] 厳密には、多重共線性は「推定した標準化偏回帰係数の標準誤差の値が大きくなる」問題を指します。
[8] 因果関係を主張するためにどのような手続きを用いるのがよいのかは、当社の以下のコラムで例を示しています。適宜参考ください;
アンケート以外のデータ収集方法:縦断的調査、実験室実験、生理学的指標、IAT、日誌法、経験サンプリング法の紹介
[9] 厳密には、ある影響指標が他の影響指標と似ており多重共線性が問題になる程度は「ある影響指標を成果指標(基準変数)に据えて、他の影響指標すべてを影響指標(予測変数)とした重回帰分析の決定係数R2の大きさ」で決まります。そのため、影響指標同士の相関が.70を多少下回っていたとしても、複数の影響指標を取り上げていた場合は上記の決定係数が大きくなりやすいため、多重共線性の問題が生じやすい状態になります。
執筆者
 能渡 真澄
能渡 真澄
株式会社ビジネスリサーチラボ チーフフェロー。信州大学人文学部卒業、信州大学大学院人文科学研究科修士課程修了。修士(文学)。価値観の多様化が進む現代における個人のアイデンティティや自己意識の在り方を、他者との相互作用や対人関係の変容から明らかにする理論研究や実証研究を行っている。高いデータ解析技術を有しており、通常では捉えることが困難な、様々なデータの背後にある特徴や関係性を分析・可視化し、その実態を把握する支援を行っている。