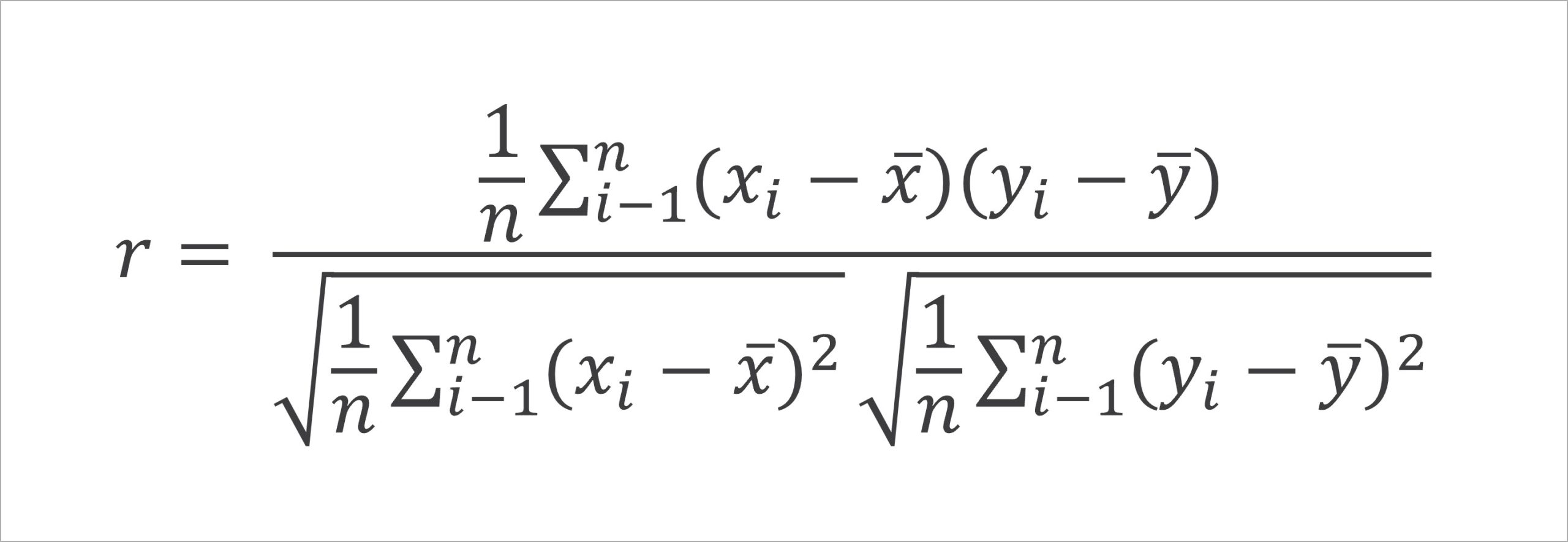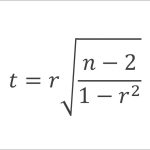ビジネスリサーチラボは、2023年4月にセミナー「人事のためのデータ分析講座 相関分析 ~2つの指標の関連を検証する~」を開催しました。「新人採用に向けて、広告への印象と自社webサイトの閲覧回数を調べよう」「研修の有効性を調べるために、事後課題の点数と翌月の営業成績の関連を確認してみよう」など、人事の仕事では2つの指標の関連を調べたい場面が多くあります。本セミナーでは、ビジネスリサーチラボ・フェローの黒住嶺が、指標の関連を調べるうえで活用できる「相関分析」について解説しました。

※本レポートはセミナーの内容を基に編集・再構成したものです。

登壇者

黒住 嶺

株式会社ビジネスリサーチラボ フェロー。学習院大学文学部卒業、学習院大学人文科学研究科修士課程修了。修士（心理学）。日常生活の素朴な疑問や誰しも経験しうる悩みを、学術的なアプローチで検証・解決することに関心があり、自身も幼少期から苦悩してきた先延ばしに関する研究を実施。教育機関やセミナーでの講師、ベンチャー企業でのインターンなどを通し、学術的な視点と現場や当事者の視点の行き来を志向・実践。その経験を活かし、多くの当事者との接点となりうる組織・人事の課題への実効的なアプローチを探求している。

相関分析とは

相関分析＝相関係数を求めること

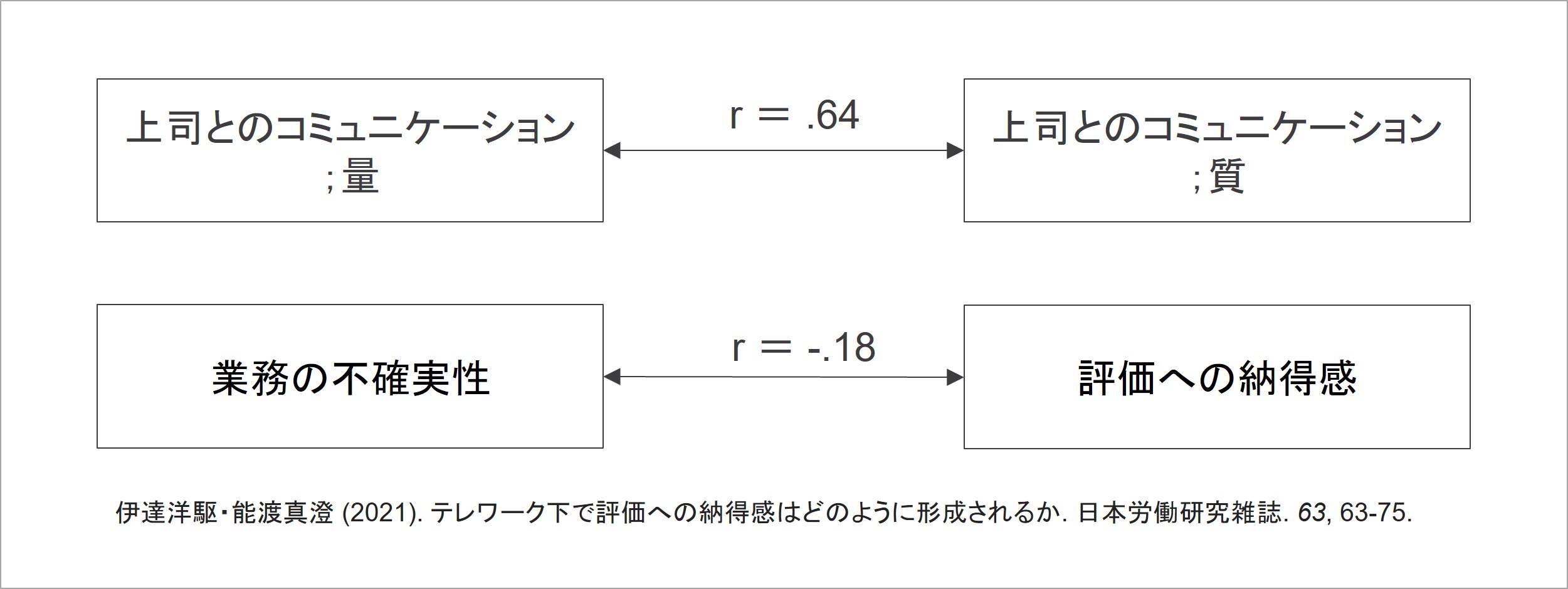
相関分析とは、二つの指標が対応する度合いを調べる分析です。具体的には、相関係数rという係数を算出することで、定量的に二つの指標の対応関係を見るということです。例えば、実際の論文では次のように表されます。

相関分析を用いることで、対応する度合いについて二つの観点を理解することが可能となります。1つ目は対応の種類で、主に三つの種類があります。

まず正の相関です。これは、一方が高いときにもう一方も高く、一方が低いときはもう一方も低い関係です。部下を鼓舞する上司の方のもとでは、部下が自分なりに仕事に関する学びを積極的に行うという例があります。次に、負の相関です。一方の値が高いときもう一方の値が低い、もう一方の値が低いときはもう一方が高い関係です。仕事にやりがいを感じていると、仕事を先延ばしないという例があります。最後は、無相関です。読んで字のごとく、対応関係がないということです。極端な例では、ある1日の気温と上司部下の関係性は無相関であると考えられます。

相関分析によってわかる2つ目の観点が、対応の強さです。相関係数には、統一された判断基準が設けられているのです。具体的に説明していきます。

前提として、相関係数には必ず「-1」から「1」の間に収まる性質があります。つまり絶対値「1」を超えず、小数点以下で表示されるため、表記の際は一の位にある「0」を割愛する習慣があります。例えば、相関係数「0.20」は「.20」と表記され、「コンマ・ニ」と読みます。

そのうえで、相関係数の強さについて、いくつかの基準が提唱されています。1つの例として、次のような4段階の区分があります。なお、絶対値で表記しているように、正の相関、負の相関のいずれでも解釈は同じです。

• r < |.20|：無相関
• |.20| ≦ r < |.40|：弱い相関
• |.40| ≦ r < |.70|：中程度の相関
• |.70| ≦ r：強い相関

相関係数の利点＝比較に使える

次に、相関係数が持つメリットを紹介します。端的に表現すると、数値を比較しやすいということです。

ここまでの内容で、相関係数は3タイプの関係を区別でき、強さの基準も提案されていることを紹介しました。加えて、これら2つの特徴は、どのくらいの対象者へサーベイを実施したかというサンプルサイズの影響や、測定に使った単位の影響を受けないという特徴も備えています。

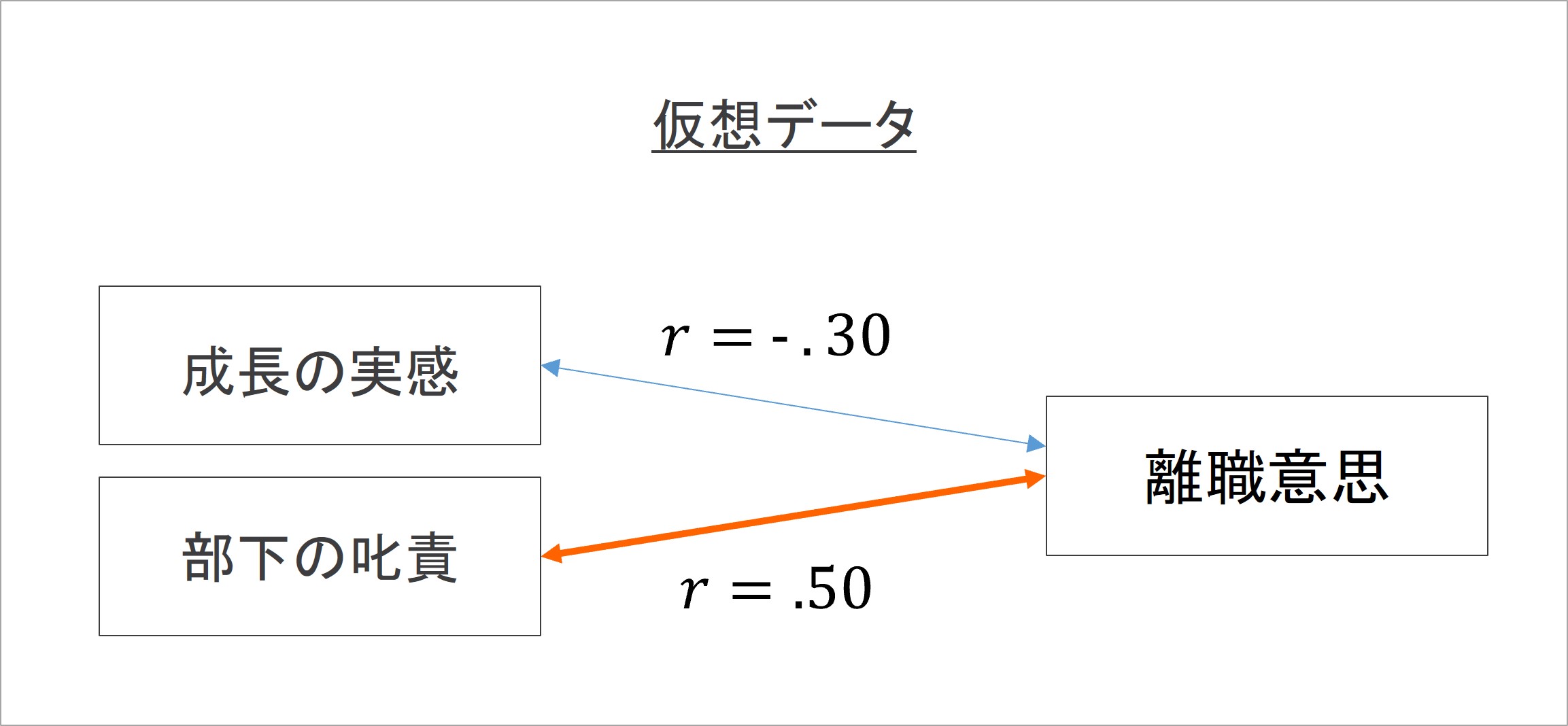
では、これらの特徴が、数値の比較にどのように有用なのかを、仮想の組織サーベイを例に考えてみます。新人の離職意思と関連する指標についてサーベイを行った結果、次の結果が得られたとします。

仕事を通して「成長を実感できている」ほど離職意思が低いことを示す結果として、r = -.30という負の相関関係がみられたとします。加えて、部下が上司から強い言葉で叱責されていると感じるほど離職意思が高いことを示す結果として、r = .50という正の相関関係もみられたとします。

この結果については、相関係数を比較することができるので、同一の組織サーベイ内での比較と、他の組織サーベイ間との比較に応用できます。前者については、例えば、より強い相関のある指標を、今後の施策に応用するという使い方ができます。成長の実感よりも先に、部下の叱責の影響が強いことを考慮して「今年度はマネジメント研修で適切な伝え方を指導しよう」という具合です。

もう一方の組織サーベイ間での比較については、例えば、組織サーベイで測定する指標の取捨選択に参照できます。例えば、昨年に先ほどの結果が得られたとすると、「今年も同じ傾向か調べたいので同じ指標を使おう」「昨年の傾向には対策も打ったので別の指標を見てみよう」と考えることができます。

相関分析の図解＝散布図に表される

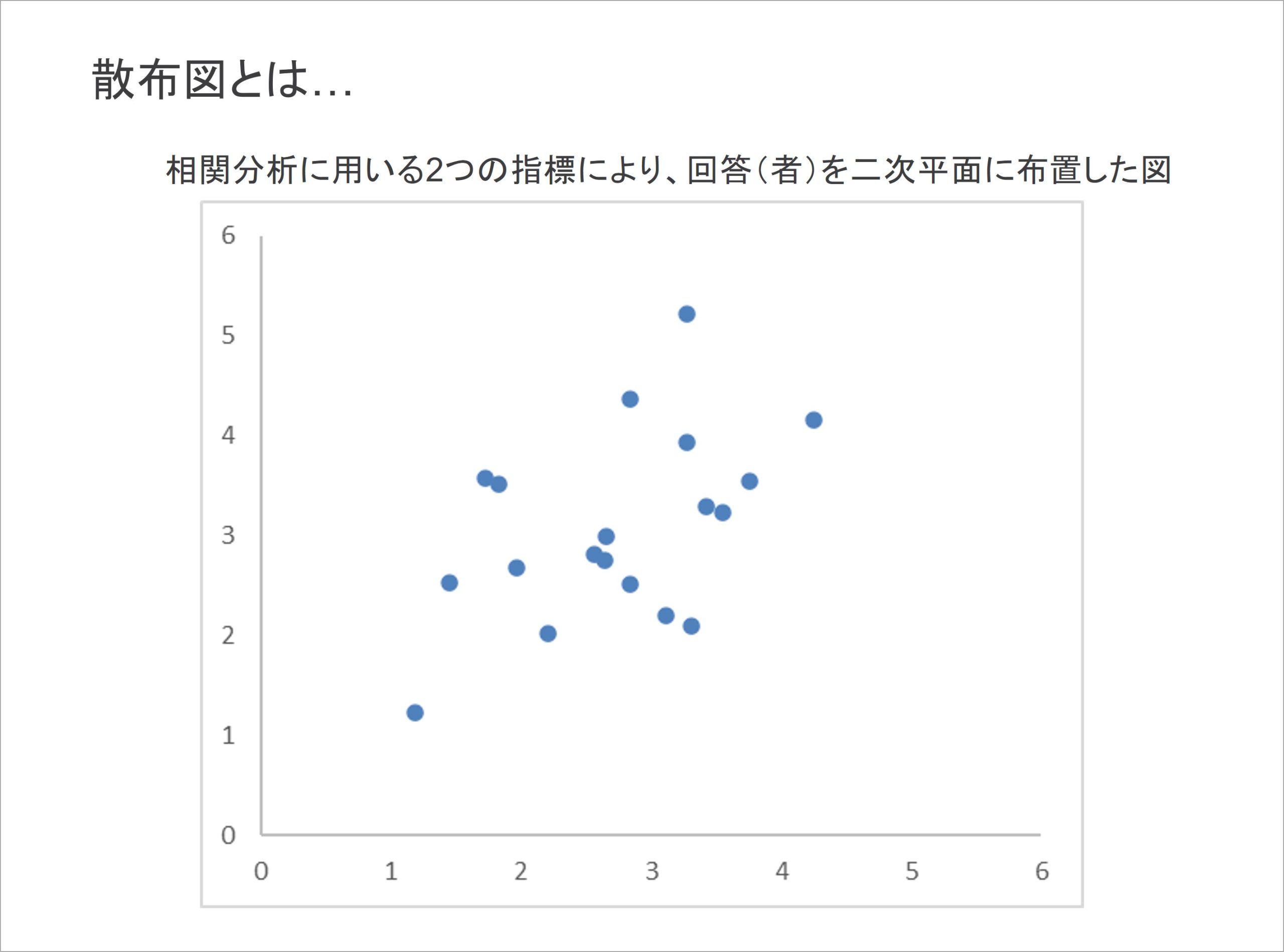
ここから、相関係数は図を用いて解釈することもできるという点を紹介します。相関係数は、次のような「散布図」によって表すことができます。

散布図では、相関分析で用いる二つの指標を、一方をx、もう一方をyと仮置きして、全回答を二次平面上に配置したものです。では、この散布図に、相関の種類と強さがどのように表れるのかを見ていきます。

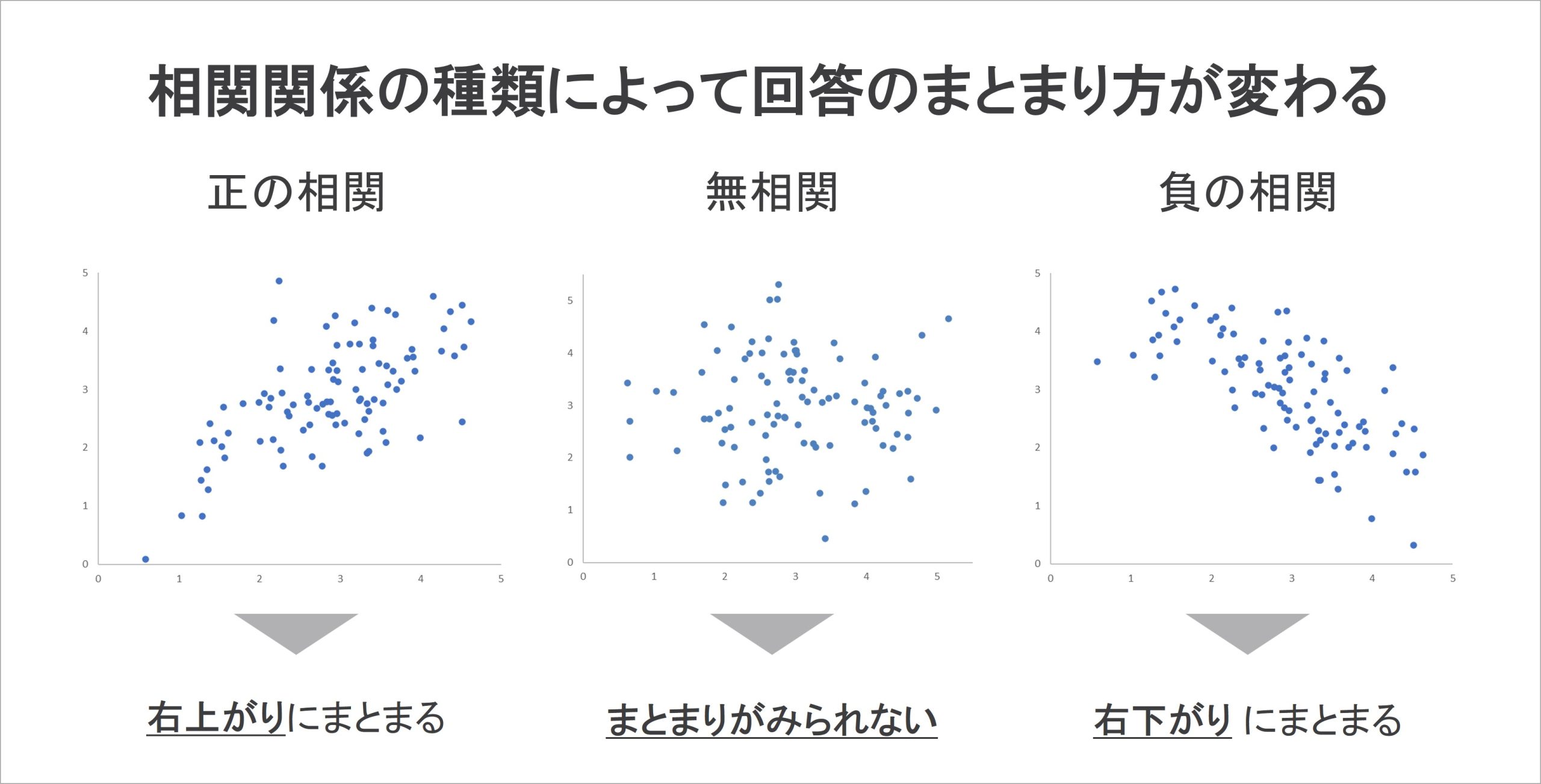
まず、相関の種類の現れ方です。相関の種類の現れ方によって全回答のまとまり方が変わります。相関関係の種類ごとに、以下のような形が現れます。

正の相関は、一方の指標xが高いときにもう一方の指標yも高く、指標xが低いときには指標yも低いという関係です。そのため、回答が右上がりの形に分布します。負の相関は、指標xが高いときに指標yが低く、指標xが低いときには指標yが高くなります。そのため、回答は全体として右下がりに分布します。最後に、無相関とは、二つの間に関係ないということです。つまり、指標xが定まっても指標yの値が定まらないのです。そのため、散布図には一定のまとまりは見られません。

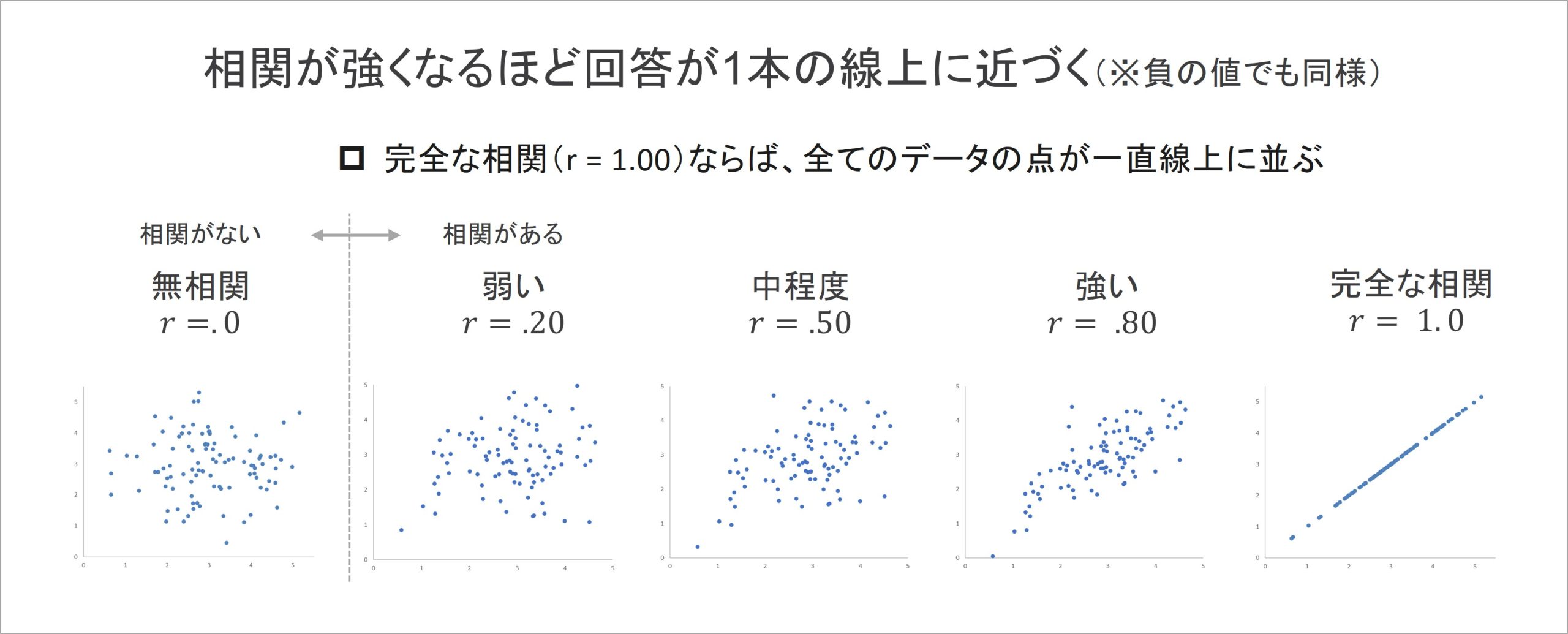
次に相関係数の強さが、散布図にどのように表れるかというと、回答が直線の形に近づいていきます。相関係数の強さのみを変えたときに、散布図は次のように変化していきます。

もし2つの指標が、最も強いr = 1.00の相関係数を示す場合、つまり完全な相関関係があるときは、指標xの値が決まると指標yの値が必ず決まるため、回答は一直線に並びます。逆に、相関が全くないr = .00の場合、回答にはまとまりがありません。そのため、その過程に当たる相関関係の場合、より強い相関がみられるほど、直線の形に近づいていくのです。

相関分析を進めるポイント

実際に相関分析の手続きを進めるうえで、確認するべきポイントは次の3つです。以降ではそれぞれの内容について説明していきます。

• 手元の二つの指標間がどのような関係にあるのかを確認する＝記述統計としての相関分析
• 手元のデータから得た結果が他の対象にも適用できるのかを確認する＝推測統計としての相関分析
• 得られた結果を額面通りに受け取って良いのかを確認する＝相関分析の注意点

記述統計としての相関分析

手元の二つの指標間がどのような関係にあるのかを確認するために必要なのが、記述統計としての相関分析です。

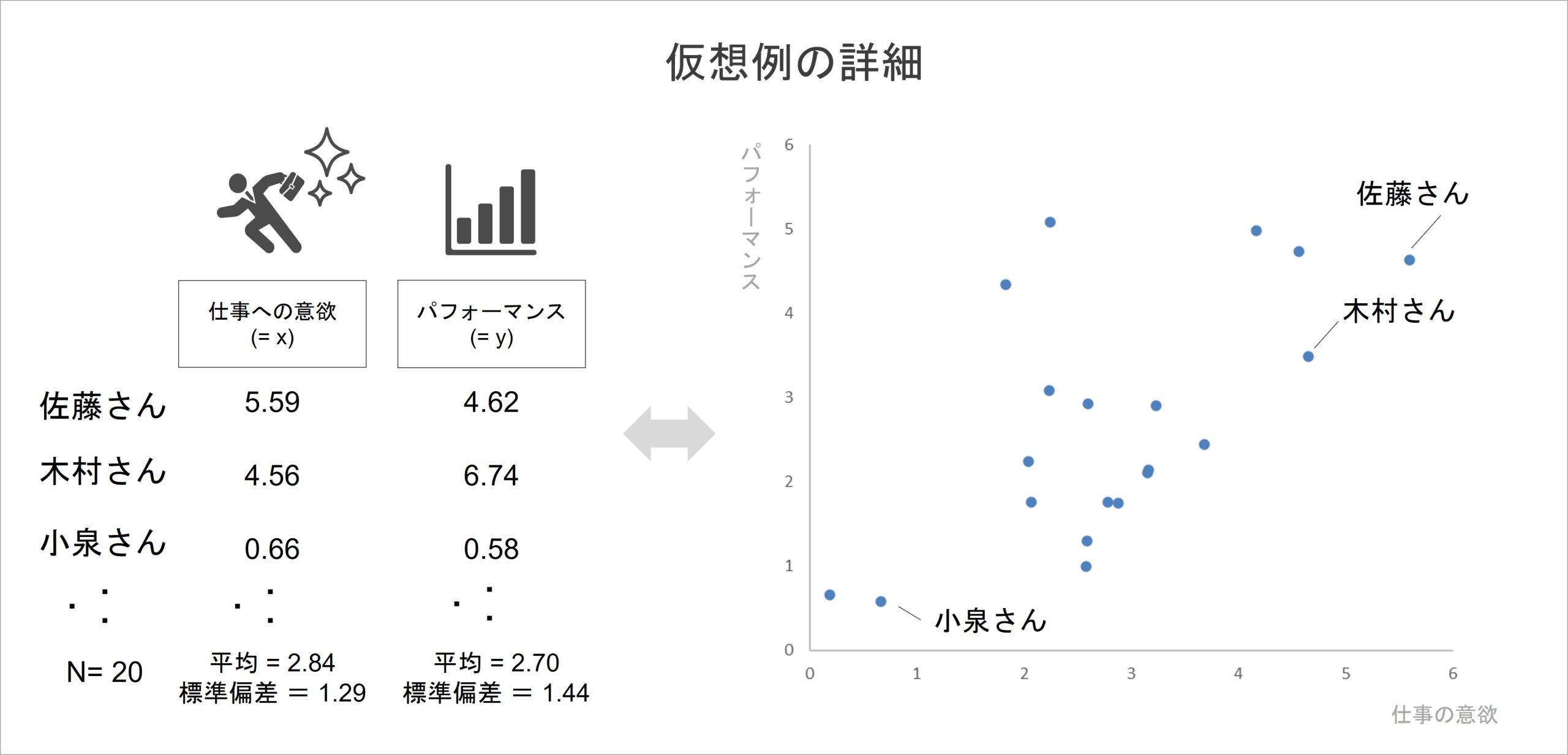
例に沿って、説明していきます。仕事の意欲とパフォーマンスの関連を調べた仮想の組織サーベイにより、以下のような結果が得られたとします。

 

 

 

仮説としては、仕事の意欲とパフォーマンスに正の相関があることを想定します。仕事に意欲を持って行って取り組んでいるならばパフォーマンスも高い、あるいは、パフォーマンスが高いので仕事に意欲的に取り組める側面もあるかもしれません。

では、実際に相関係数を求める数式を見ていきます。相関係数は、次の式で表されます。

この数式は、分子の部分と分母の部に分けて見ていくことで、その意味するところが分かりやすくなります。以降ではそれぞれについて解説します。

分子の計算：指標の関係性を数量化する

分子の計算では、2つの指標の関係に応じて、特定の値を取るように数量化する処理を行っています。具体的には３つのステップに分かれます。

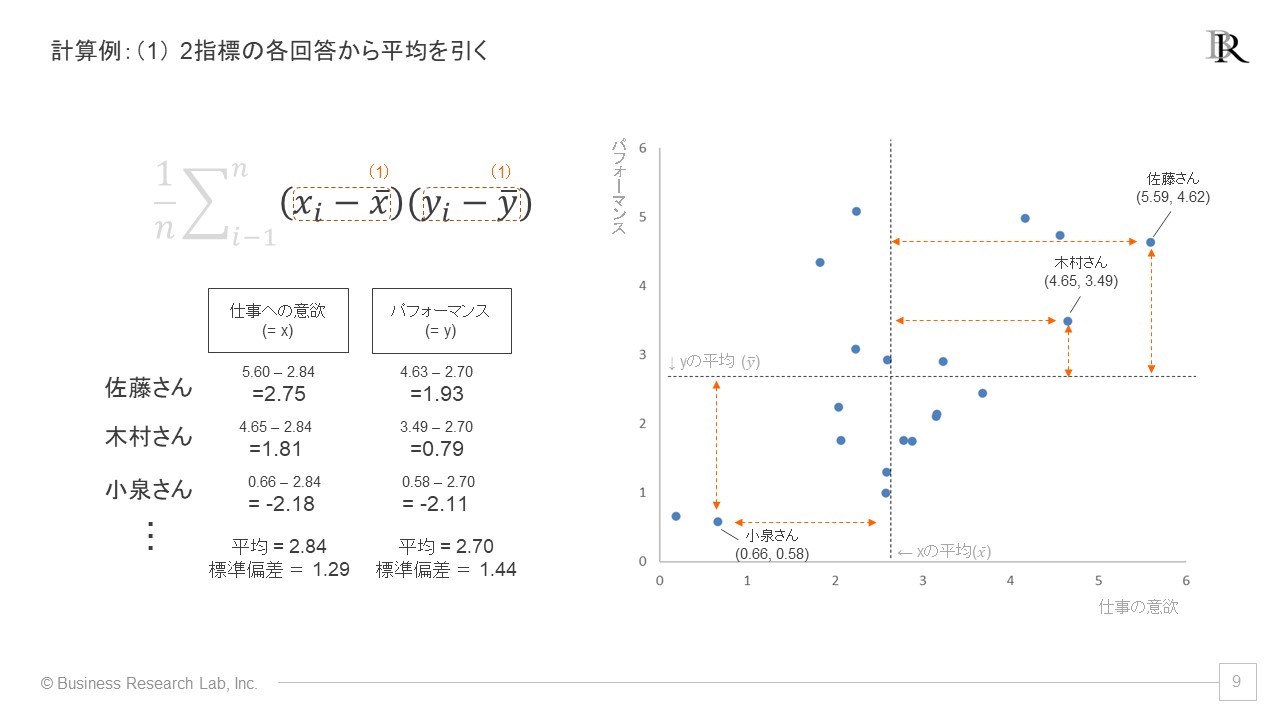
第1ステップでは、各回答の2つの指標から、それぞれの指標の平均値を引きます。仕事の意欲とパフォーマンスの仮想の例に沿ってみると、以下のように計算が行われます。

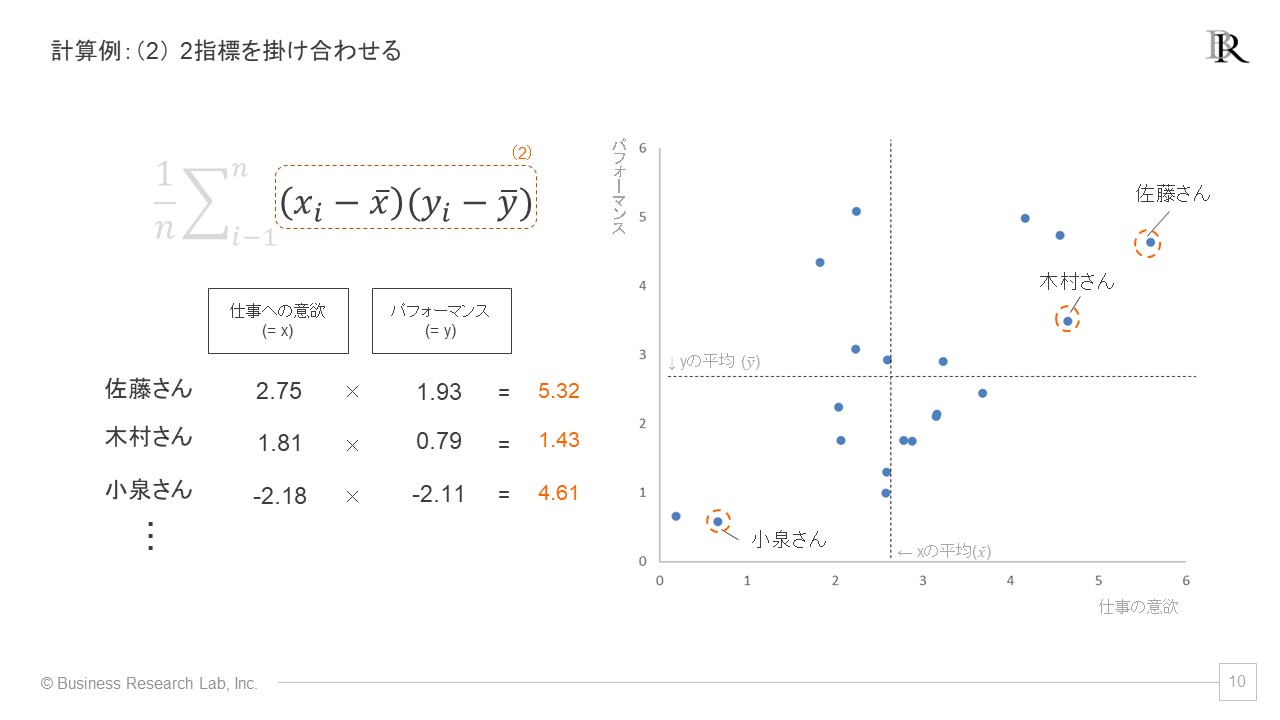
第2ステップでは、第1ステップで得られた値を掛け合わせます。これにより、各回答者の2つの指標を合成した、1つの解を得ることができました。同様に先ほどの例でみると、以下のような計算となります。

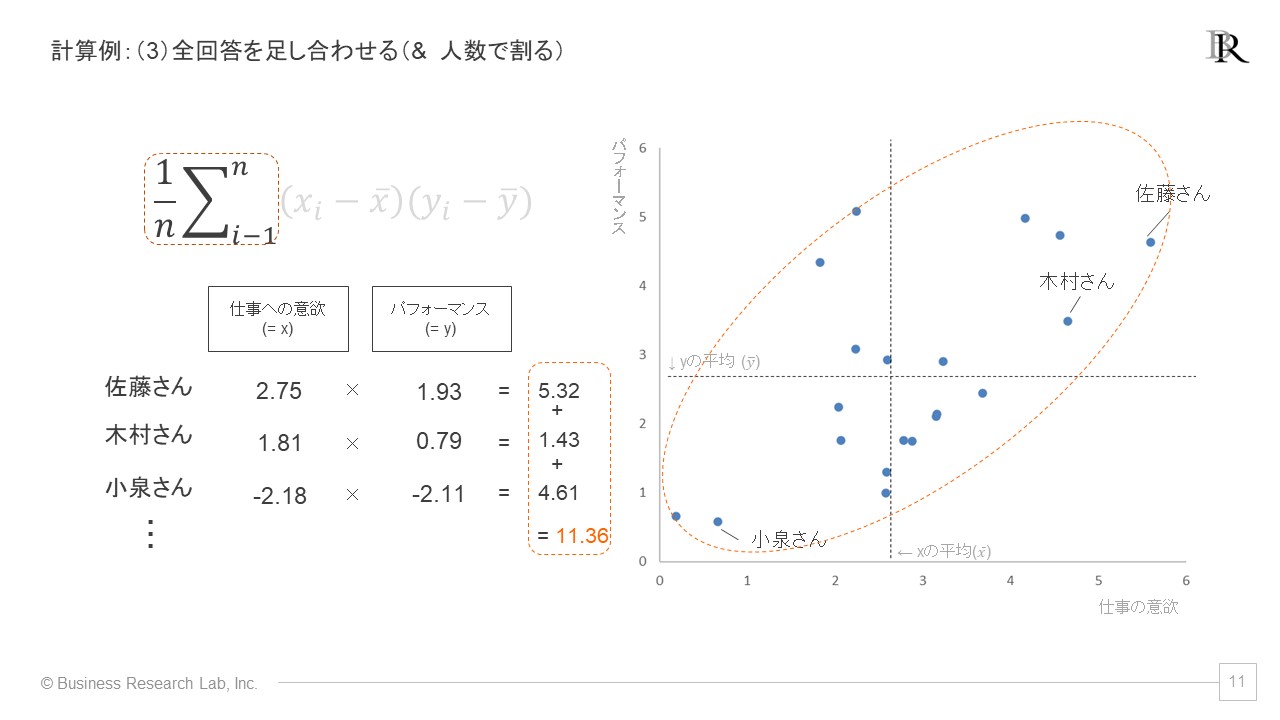
第3ステップでは、第2ステップによって得た解を、全回答者分足し合わせ、サンプルサイズで割ります。これにより、全ての回答を反映させた、2つの指標の関連に関する1つの値を得ることができました。計算例は、以下のようになります。

また、ここまでの計算によって求められる分子の解には、「共分散（きょうぶんさん）」という特別な名前が付けられています。共分散というキーワードは、統計的な手続きの多くに関わるため、覚えておいて損はないでしょう。

共分散が持つ特徴

共分散は、2指標の関連を数量化するうえで、便利な特徴を持っています。2つの指標が正の相関関係にあるほど、正の大きな値をとり、逆に負の相関関係にあるほど、負の小さな値をとるのです。その理由を、散布図と併せて紹介していきます。

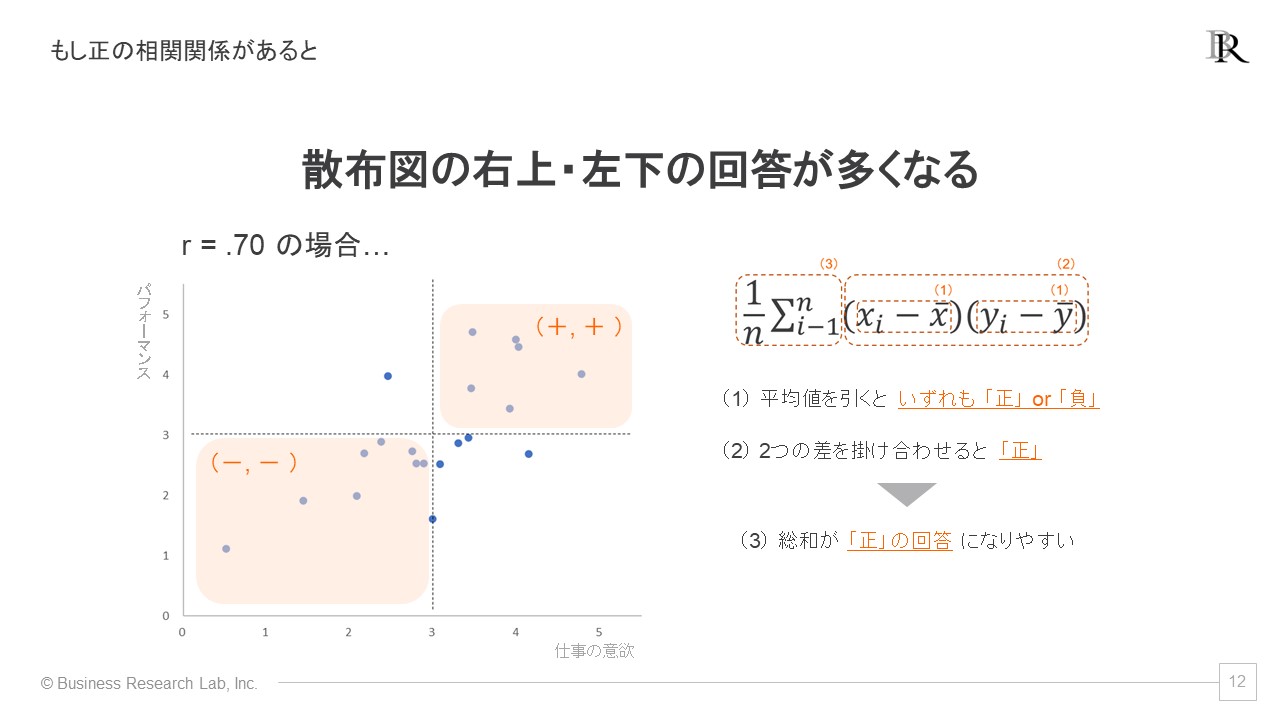
まず、正の相関がある場合の散布図は右上がりになると説明しましたが、このとき回答者全体を、指標xとｙの平均値で分割してみると、散布図の右上と左下に布置される回答が多くなります。これらの回答は、2指標とも平均値より高い、または2指標とも平均値より低いとも言い換えられます。

このような状況で共分散を計算してみましょう。ステップ1は、指標x、yともに平均値よりも大きい・または小さいため、得られる2つの解が共に「正」あるいは「負」の値となる回答が多くなります。そのため、続くステップ2 では、「正×正」または「負×負」の計算を行う回答が増えるので、解の多くが「正」の値になります。その結果、ステップ3では、算出された総和が「正」の値になりやすいのです。

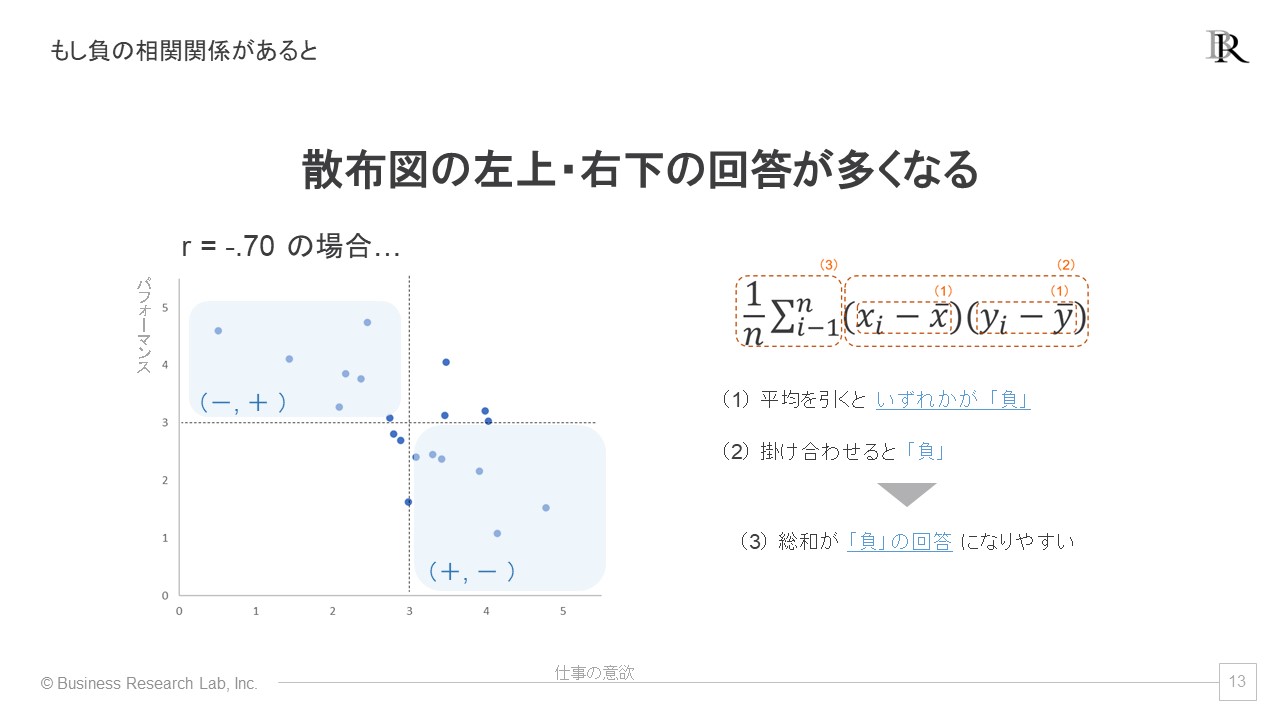
続いて、負の相関がある場合の散布図を見てみます。先ほどと同様の手続きで回答者を分割すると、散布図は左上と右下の回答が多くなります。

このとき、散布図の右下に布置された回答は、指標xは平均値よりも大きく、指標yは平均値より小さいという状況です。逆に、左上に布置された回答は、指標xは平均値より小さく、指標yは平均値より大きいといえます。

ステップ1では、指標x、yのうち、計算した解のいずれかが「正」、もう一方は「負」という回答が多くなります。そのため、ステップ2では、「正×負」の計算を行う回答が増え、解の多くが「負」の値をとります。そしてステップ3では、総和が「負」になりやすいのです。

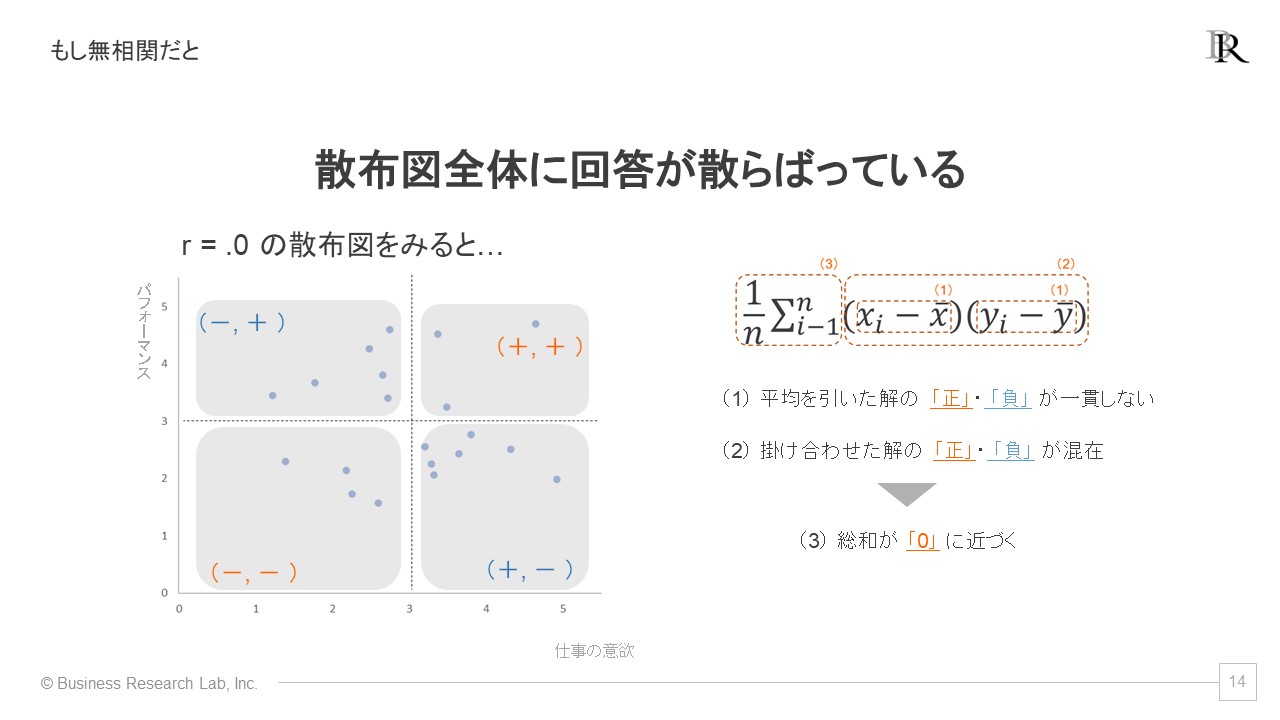
最後に、無相関の場合は、散布図にまとまりがないという状況です。そのため、平均値による分割を行っても、いずれの箇所にも回答者が散在していることになります。

この状況下では、ステップ1で求める両指標の解の「正」・「負」が一貫することはありません。そのためステップ2では、「正」と「負」の解が混在することになります。その結果、ステップ3の総和が「0」に近い値になりやすいのです。

分母の計算：共分散から単位の影響を取り除く

分子（＝共分散）の計算の説明を終えたところで、改めて相関係数全体の数式を確認します。ここからは、分母の計算について解説していきます。分母では、共分散から「単位」の影響を取り除くという計算を行います。

さて、共分散の分析の時点で「回答全体を数量化できたので一件落着」と思われた方がいるかもしれません。ただ、共分散には、測定した指標の「単位」の影響を受けるという限界があります。

なぜ単位の影響を考慮するべきかを理解するため、次のような例を考えてみます。ある人物の同じ特徴について、5段階で答える心理尺度と、特定の行動を1日にする頻度という行動指標によって、2通りで数量化するとします。この場合、心理尺度による回答は最大値「5」を超えませんが、行動指標は最大値がないため、場合によって「5」よりも大きな値をとることになります。つまり、用いた単位が変われば、同じ人の同じ特徴を測定したとしても、その数値は変わってしまうのです。

共分散も、上記のような単位の影響を受け、計算に用いた指標の単位によって、値の意味が変わってしまいます。つまり、共分散も関係性の強さを数量化してはいるものの、異なる尺度を用いて計算された共分散同士は、単位が異なるためにその強さを比較することができません。

そこで用いられるのが、「標準化」という手続きです。標準化とは、元々の得点を、一定の平均値と標準偏差をとるように変換していくことです。計算例としては、次のようなものがあります。

上記の計算例では、素点（元々の値）から平均値を引き、標準偏差で割るという処理を行うことで、平均0、標準偏差1に変換されています。他にも、学力テストで用いられることの多い偏差値も、平均値50、標準偏差10になるように変換した指標であり、標準化の一部であるといえます。

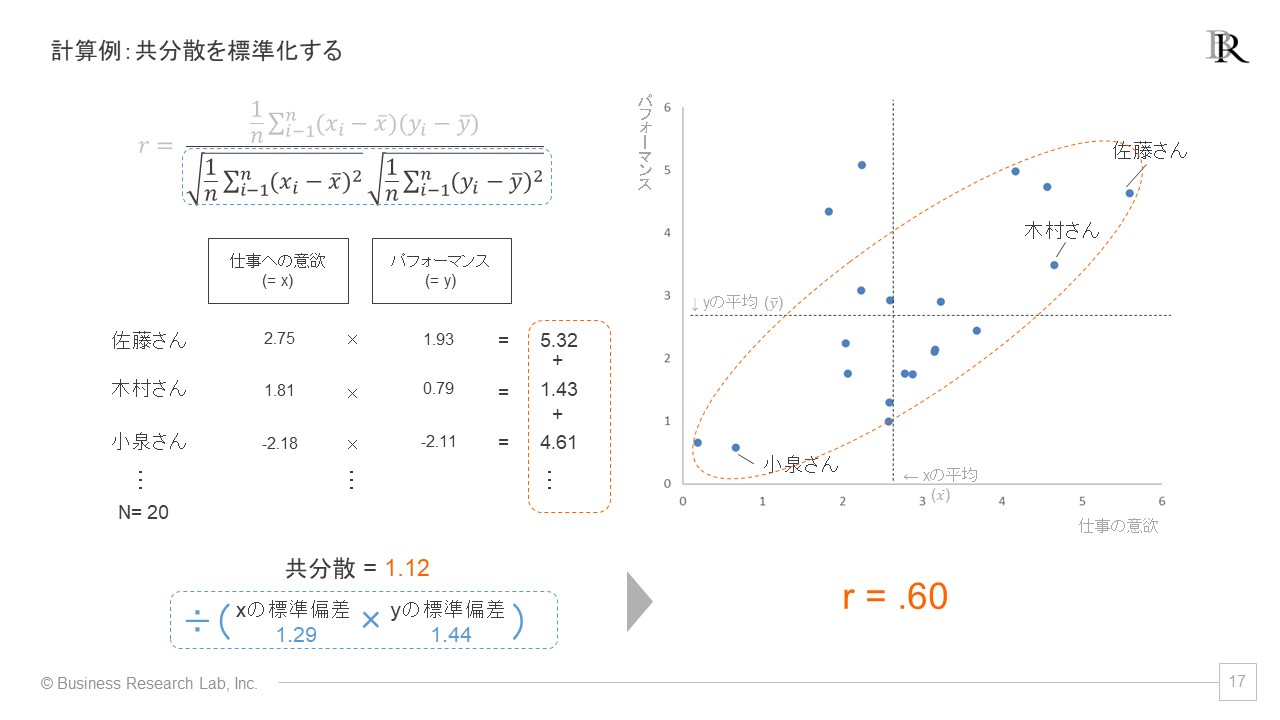
この手続きについて、仕事の意欲とパフォーマンスの関連を測定する仮想のサーベイに沿って計算した例を示します。回答者が20名で、分散が1.12と算出されたとします。このとき、指標xの標準偏差が1.29、指標yの標準偏差が1.44であったとすると、相関係数rは.60と算出することができます。

推測統計としての相関分析

推測統計とは

相関分析を進めていくうえで確認するべきポイントの2つ目が、推測統計としての相関分析です。これは、手元のデータから得られた結果を、他の対象にも適用できるのかを確認する必要があるということです。ここからは、推測統計について簡単に復習していきます[1]。

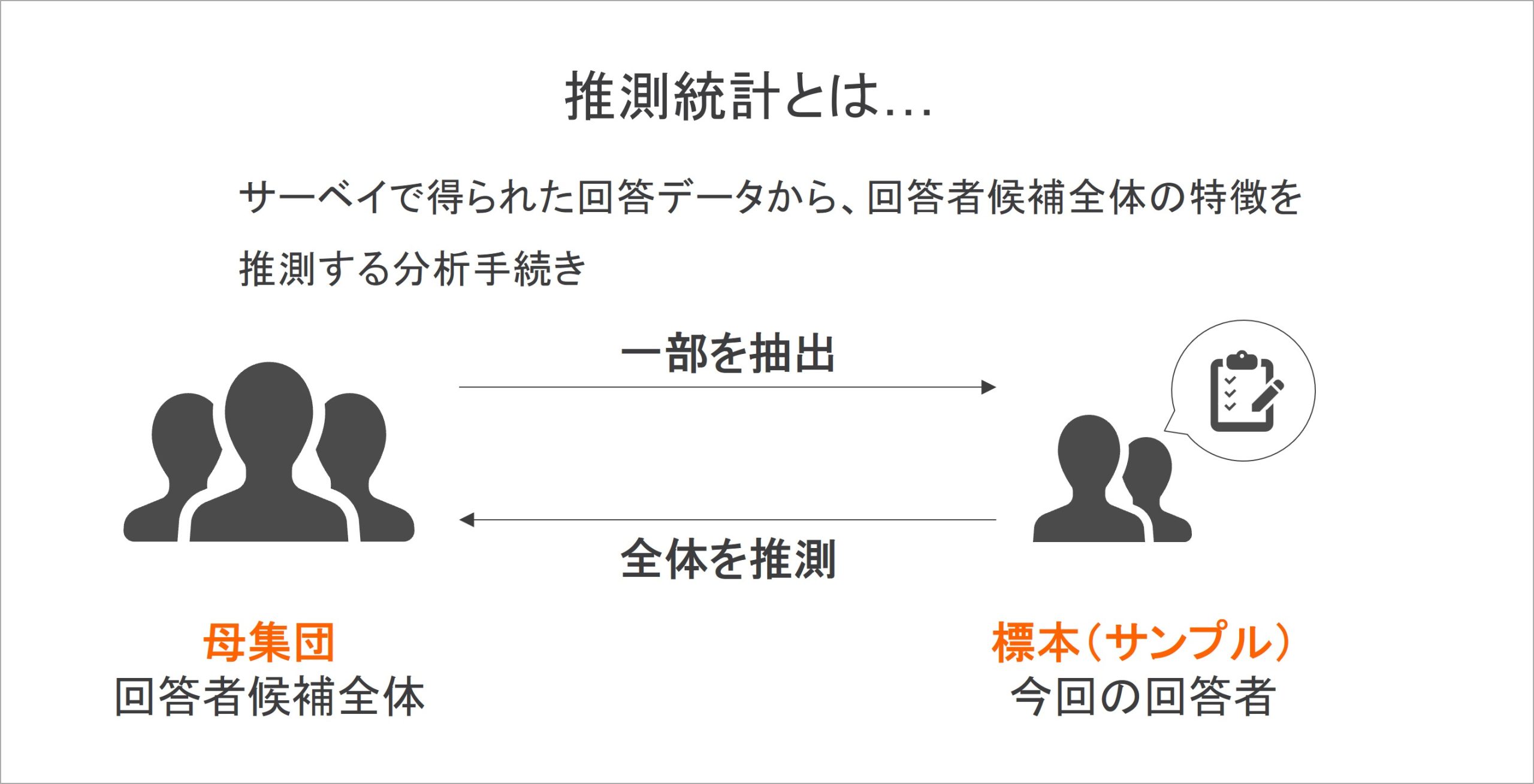
まず、手元のデータを提供してくれた回答者を「標本」と呼びます。対して、標本だけでなく回答者の候補になる人たち全体を「母集団」と呼びます。先ほど説明した記述統計は、得られたデータの分析結果を通して、標本の特徴を確認している作業といえます。

ただし、記述統計はあくまでも標本の特徴であり、それ以外の回答者を含む母集団でも同じような特徴があるとは言えないのです。また、母集団の特徴は、基本的には直接把握することができません[2]。そのため、標本のデータから母集団の特徴を推測することが必要であり、その分析を「推測統計」と呼ぶのです。

帰無仮説を立てる

推測統計は主に3つのステップで進めます。

第1のステップは、帰無仮説を立てることです。これは、「母集団の相関が『0』と仮定する」ことだとも言い換えられます。

帰無仮説とは、検証する目的に対して「無に帰するべき状態」を示した仮説という意味です。相関分析の場合は、「標本では二つの指標に相関係数が確認されたが、母集団では相関がないかもしれない」と考えるので、「母集団の相関＝0」が帰無仮説となります。このように、最初のステップとして帰無仮説を立て、それを棄却できるかを、次のステップ以降で検証します。

検定統計量を計算する

第2のステップは、検定統計量を計算することです。前提として、標本で見られた相関が、母集団でも同じように確認できるとは限らないことを説明しました。では、標本と母集団の関係性について、より具体的にイメージしてみます。

ここで、サイコロを振って「3」の目が出る確率について考えてみてください。細工のないサイコロであれば、理論的には6分の1の確率になるはずです。この時、理論的な確率を母集団の特徴、実際にサイコロを振ったときの確率を標本の特徴、と置き換えることができます。

では、例えばサイコロを60回振ったとして、必ず「3」の目が10回出るかといえば、そうとも限りません。他の目が沢山出ることもあれば、「3」の目が10回以上出ることもあるでしょう。つまり、母集団の特徴を、標本は完全には反映しきれないのです。このことを踏まえると、母集団の特徴から、標本がどう変わるのかを考慮することが必要だといえます。

この作業を担うのが、検定統計量の計算です。検定統計量とは、帰無仮説が真であると仮定したとき、今回得られた結果と同じかそれ以上に極端なデータが得られる確率「p値」を計算するために算出する指標です。相関係数の検定統計量は、以下の数式によりt値で表せることがわかっています。

上記の数式のうち、rは標本の相関係数、nは標本のサンプルサイズを表しています[3]。この式によって、得られた標本データにおける検定統計量を計算することができます。

有意確率（p値）を計算する

第3のステップは、有意確率p値を計算することです。これは推測統計の最後の工程として、得られた標本から母集団の特徴について考察する段階とも言えます。

第2ステップで求めた検定統計量t値は、帰無仮説が正しいことを前提とした母集団と、サーベイで得られた標本データの対応関係を仮定しています。[4]。この知見を利用することで、今回の標本から確認されたのと同程度、あるいはそれ以上の大きさの相関係数が、「母集団の相関＝0」という前提の下でどの程度の確率で得られるのかを計算することができます。

計算例として、仕事の意欲とパフォーマンスに関する仮想のサーベイ結果を再び確認します。標本の相関係数ｒは.60であり、サンプルサイズは20と仮定しました。この時、先ほどの検定統計量およびp値を求めると、以下のようになります。

このようにして得られたp値を用いて、帰無仮説が棄却されるかを判断します。具体的には、p値が「5％」を下回っているかを確認し、もし下回っている場合には帰無仮説を棄却します。この5%という基準は、主に心理学や経営学といった学術領域で慣例として用いられている基準です。そして、標本から得られた結果が、推測統計からみて意味がある、いわゆる統計的に有意な結果だと判断します。上記の計算例はp値が「0.005」つまり0.5％であるため、有意な結果が得られたといえます。

では、なぜp値が5%を下回ると、帰無仮説を棄却できるのでしょうか。p値の計算は、帰無仮説が「正しい」という前提のもとで行われています。仮に、標本から得られたp値が5％を下回ったとすると、それは「5%未満でしか起こらない稀な結果」が得られたことになります。このことから、「滅多に起きえないような結果が起きるのならば前提に誤りがあるだろう」と判断できるのです。

相関分析の注意点

相関分析を進めていくうえで確認するべきポイントの3つ目のポイントは、得られた結果を額面通り受け取ってよいのかを確認することです。これは、相関係数そのもののみを確認するだけでは、実態を見誤る可能性があるためです。

人の特徴や現象を考えると、測定する二つの指標がシンプルな対応関係になっているとは限りません。しかし統計ソフトを使う場合などは、どのような指標同士であっても、相関係数を計算すること自体は可能です。そのため、数値だけを見てしまうと、実態を見誤る可能性があるのです。

つまり相関分析の結果を解釈するうえで、指標の関係を誤解していないかを確認するためにいくつかの注意点を抑えておくことが重要なのです。以降では、その代表例を三つ紹介します[5]。

特異な散布図になっていないか

1つ目の注意点は、特異な散布図になっていないのかという点です。これは、相関係数が直線的な関係以外を数値に反映しきれない、という限界があるため注意するべきといえます。

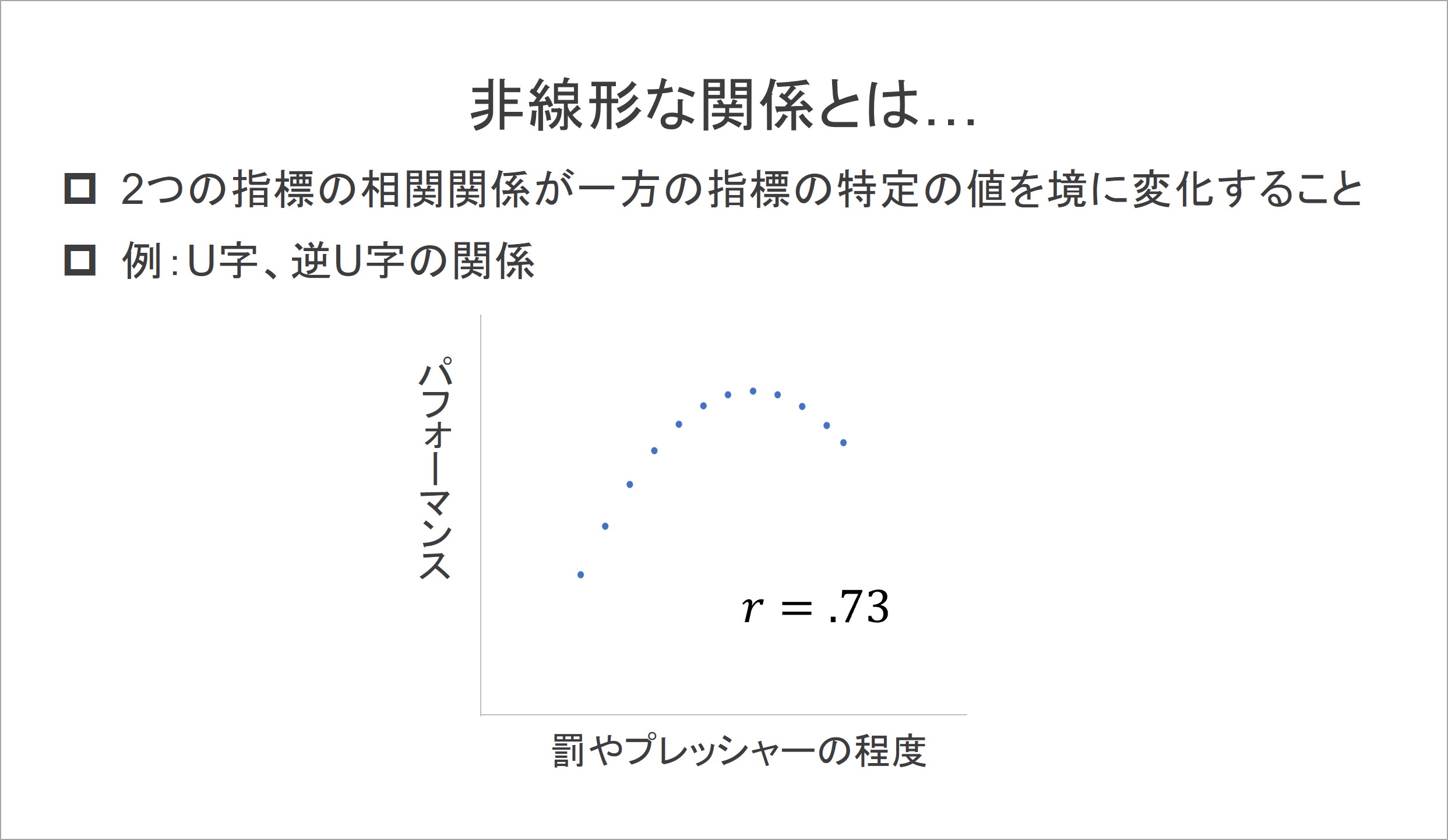
例えば、2つの指標が非線形的な関係になっている場合があります。非線形な関係とは、2つの指標の相関関係が、一方の指標の特定の値を境に変化することです。代表的な例として、パフォーマンスに対する「罰」や「タイムプレッシャー」の効果が挙げられます。

例えば、単純な課題に取り組むとき、罰の重さやタイムプレッシャーが適度なうちは「失敗しないように」と気をつけるので、その程度が高まるごとにパフォーマンスも高まっていきます。しかし、過度になってくると、失敗のリスクが焦りを生むなどの理由から、パフォーマンスが下がることが考えられます。この関係を散布図に表すと、以下のような図となります。

 

上記の散布図を見てわかるように、2つの指標の関係はアルファベットの「U」をひっくり返したような逆U字といえる関係になります。しかし、仮にこの散布図の相関係数を求めると「.73」という、まるで強い相関関係があるかのように計算されてしまいます。

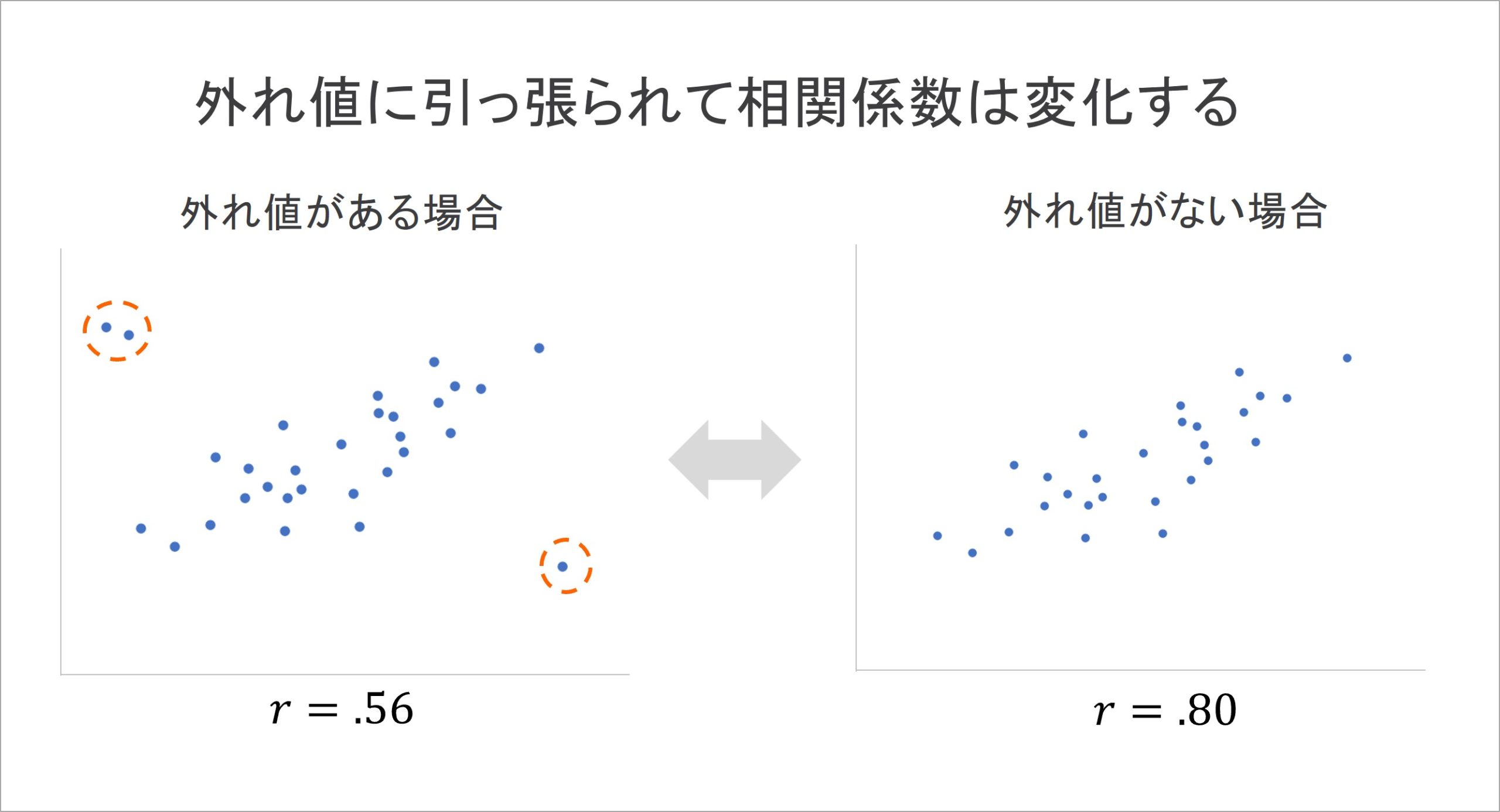
特異な散布図に関するもう一つの例として、外れ値の影響が挙げられます。例えば、以下に示すように、橙色の破線で囲った回答を除くことで、相関係数は大きく向上します。

一方で、何をもって外れ値とするのか、その判断基準は分析者にゆだねられている部分があります。相関係数が外れ値（のように見える値）の影響を受けるということには注意が必要といえるでしょう。

「第三の変数」が存在していないか

2つ目の注意点が、「第三の変数」が存在していないかという点です。これは、算出された相関関係が、実際には存在しない「見せかけ」かもしれないことから注意が必要になります。

「第三の変数」とは、相関関係を想定する二つの指標とは別に、その二つの指標に影響を与えている別の指標のことです。もしこうした指標が存在していると、その変化に伴って、他の2つの指標も変化します。そのため、実際には相関関係がなかったとしても、一定程度の大きさの相関係数が算出されてしまうのです[6]。

標本が偏っていないか

3つ目の注意点は、標本が偏っていないかという点です。偏りが生じている場合には「選抜効果」が起きる可能性があるためです。

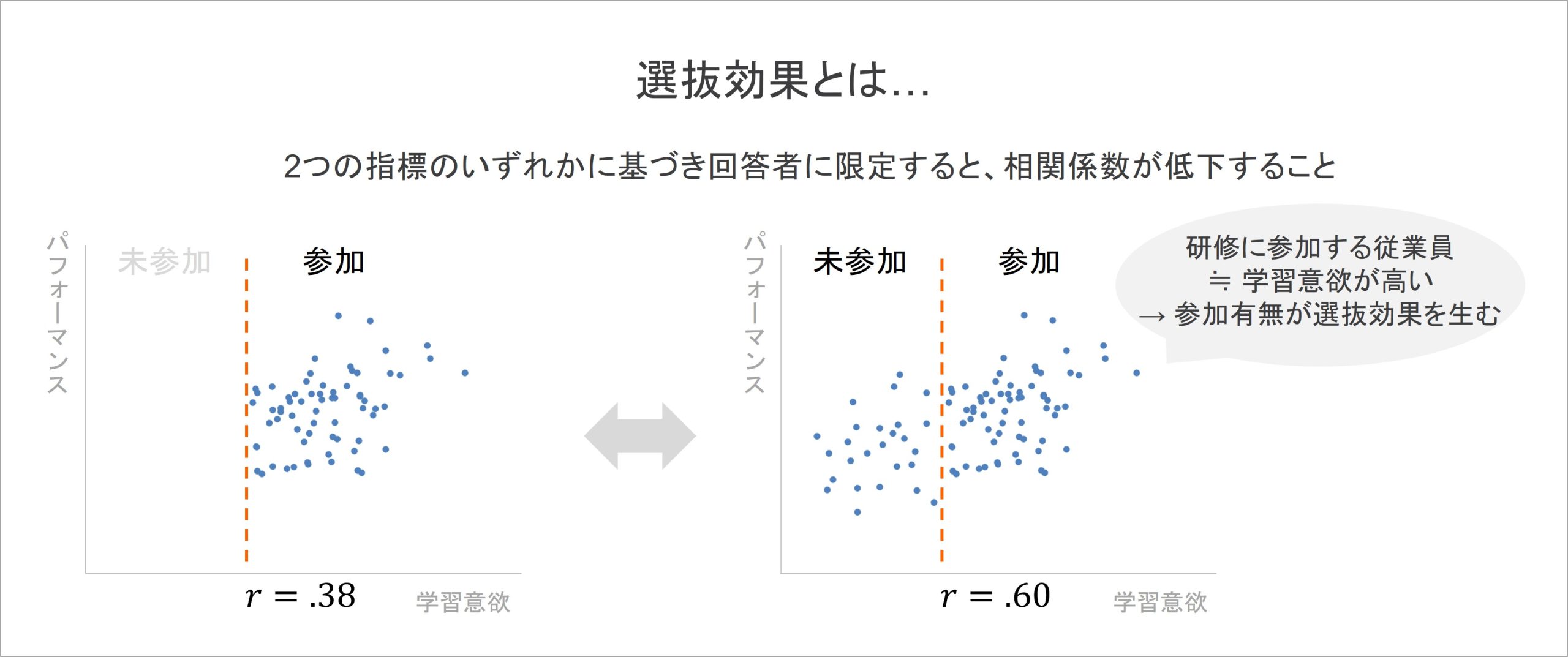
例えば、研修に参加した従業員の学習意欲と業務のパフォーマンスについて相関分析を行ったとき、以下の左図のような結果が得られたとします。分析の結果、相関係数は確認されたものの、r =.38と弱い値にとどまっています。実はこの時、「研修に参加したかどうか」という点で、回答者の偏りが起きていると考えらます。

 

まず、研修に積極的に参加する方々は、元々学習意欲が高く、パフォーマンスも高い可能性があります。反対に、研修に参加していない人は、学習意欲があまり高くなく、パフォーマンスも低いと予想できます。

仮に上記の予想が正しく、研修に参加していない従業員にもアンケートを実施できて、上図の右側に示した散布図のデータを得られたとします。このデータについて相関係数を計算すると、その値はr =.60の強さを示しました。研修の参加者に限定されたときの結果に比べて、大きな値になっていることが分かります。

このように、回答者を限定することで相関係数が低下することを「選抜効果」と呼びます。上記の例のように、気付かないうちに選抜が起きてしまうことも考えられるため、分析時に注意が必要です。

3つの注意点への対策

ここまで挙げた注意点について取るべき対策をまとめると、やはりサーベイの実施前によく検討する、という点に集約されます。分析の段階でも、一定の対処は可能です。しかし、事後的にできる対処には限界があるため、サーベイを実施する以前に対処することが必要なのです。

例えば、回答者を増やすよう努力することで、得点の分布が連続的になることが期待され、外れ値の影響を減らせる効果が見込めます。また、回答者が偏ることで選抜効果が起きないようにするため、回答者の属性や所属先が多様になるようサーベイを実施することが必要です。さらには、「第三の変数」の影響を取り除くためには、事前にその有無を検討し、「第三の変数」自体を測定するための指標をサーベイに組み込むことが必要です[7]。

Q&A

Q1.推測統計で有意にならなかったため、同じ質問項目で同じ母集団に回答を促し、回答者数を増やすことは問題ないでしょうか

前提として、サーベイを実施する前に、仮説を検証するうえで適切なサンプル数を決めておく「例数設計」を行うことが望ましいでしょう。計画中のサーベイと類似した過去のサーベイや学術研究を参照することで、どのくらいのサンプル数が必要なのかを確認することができます。

例数設計に沿ってサンプルサイズを確保しても、想定した仮説が支持されなかった場合は、得られた結果と真摯に向き合うことが望ましいといえます。事前によく検討された仮説だったとしても、実際に測定した結果が、その仮説で見落としている何らかの実態を捉えている可能性があります。

また、推測統計の限界として、サンプルサイズを増やすと結果が有意になりやすいことが指摘されています。例えば「統計的に有意だから」という一点張りで、弱い相関係数についても関連を主張してしまうと、積極的に考慮する必要のない値に気を取られて実態を見誤る危険があります。あるいは、「結果を有意にしたい」という理由でサンプルサイズを増やすことは、推測統計の誤用であり問題のある行為と報告されており[8]、行うべきではないでしょう。

Q2. 「見せかけの相関」はどのように見極めればよいか

万能の切り札はないのですが、学術研究や自身のこれまでの経験を通して、「第三の変数」となりうる指標に関する見識を深めておくことは有効と考えられます。また、得られたデータや分析結果を、学術知や実践知と照らし合わせたときに覚えた違和感を掘り下げることも、意外な「第三の変数」の発見につながるかもしれません。

Q3. 回答者を増やす努力をする上で必要な回答者の目安が知りたい

方法として「検定力分析」を行うことで、過去のサーベイや研究で確認されたのと同程度の相関係数を再現するのに適切なサンプルサイズを確認することができます。詳細は割愛しますが、多くのサーベイで用いられる心理尺度同士の相関が「.02」であることと、統計的に有意であると判断する基準は「5％」を踏襲してこの分析を実施すると、大体80名以上いれば、同程度の相関係数を再現するのに問題がないといえます。

Q4. 自社で行った組織サーベイの結果を「40名の相関分析でr = .79だったので強い相関」と強調したが問題なかったか

自社で行ったサーベイの結果を社内で共有・活用することや、相関係数の解釈については問題ないでしょう。記述統計として、確かに得られた結果であるためです。

ただし、サンプルサイズか大きくないので、他の測定でも再現されるかどうかという点では注意が必要です。施策に応用するには、結果を過信しないようにして、場合によっては推測統計を改めて実施するのが良いでしょう。

---

 脚注

[1] 詳しくは当社のコラム「人事のためのデータ分析入門：人事のためのデータ分析講座「統計的に有意」を学ぶ（セミナーレポート）」を参照ください。

[2] 例えば「2023年度に入社した新人」のように、母集団の範囲が小さく具体的な場合には、対象者全員の回答を得ること（「全数調査」と呼びます）もできるかもしれません。一方で、「来年度の採用候補者」のように、母集団の範囲が大きく抽象的な場合には、全ての対象から回答を得ることは不可能です。そのため、標本に対する推測統計を用いた検討が必要になるのです。

[3] 「なぜ、どのようにt値で表すことができるのか」は、より細かい知識に当たりますので、本コラムでは割愛しますが、以下の資料が参考になります；南風原朝和（2002）心理統計学の基礎――統合的理解のために――　有斐閣．

[4] 帰無仮説の下で得られる標本の結果が、どのような確率でどのような値になるのか、その対応を数量的に表すものを「確率分布」と呼びます。t値は「t分布」という確率分布に従うことがわかっているため、特定のt値に対応するp値を計算することができるのです。

[5] 本コラムで取り上げるほかにも、相関分析において注意するべきポイントはいくつか存在しています。より詳細な内容は、当社のコラム「人事のためのデータ分析入門：「相関」とは何か（セミナーレポート）」を参照ください。

[6] 相関係数に対する「第三の変数」の影響やその対処方法については、当社のコラム「統制とは何か」を参照ください。

[7] サーベイにおいて「第三の変数」の影響を取り除く方法として「統制」が挙げられます。詳細は、当社のコラム「統制とは何か」を参照ください

[8] 推測統計において、分析者に都合の良い結果を得ることを目的とした一連の行為は「p-hacking」と呼ばれ、近年大きな問題点として注目されています。詳細は次の論文が参考になります；藤島 喜嗣・樋口 匡貴（2016）．社会心理学における “p-hacking” の実践例. 心理学評論, 59(1), 84-97. https://doi.org/10.24602/sjpr.59.1_84