2025年5月29日
外れ値:その理解と対応
人事担当者が扱う従業員の給与、業績評価、勤怠情報などのデータには、「外れ値」と呼ばれる特殊なデータが含まれることがあります。外れ値とは、他のデータから大きく離れた値のことで、分析結果に大きな影響を与える可能性があります。
例えば、ある部署の平均給与を計算する際、通常とは比べものにならないほど高額な報酬を得ている人のデータが含まれていた場合、その部署の平均給与は実態とかけ離れた高い数値になってしまいます。外れ値の存在に気づかずにデータ分析を進めると、間違った結論を導き出し、適切でない施策につながるリスクがあります。
本コラムでは、外れ値について解説します。外れ値とは何か、どのような影響をもたらすのか、どのように検出し対処すべきかについて説明していきます。
外れ値とは
外れ値とは、データの集合の中で他の大多数のデータから著しく離れた値のことを指します。人事データの文脈で考えると、例えば、従業員の年間残業時間のデータの中で、大半の従業員が20時間から60時間の範囲内にある中で、200時間を超える従業員がいた場合、その200時間超のデータは外れ値として扱われるかもしれません。
外れ値は、様々な理由によって生じます。データ収集や入力の際のエラーによって、外れ値が生じることがあります。例えば、給与データを入力する際に、桁を間違えて0をひとつ多く入力し、本来の10倍の額で入力してしまうようなケースが考えられます。また、勤怠管理システムなどを使用している場合、機器の故障や設定ミスによって、実際とは異なる勤務時間が記録される可能性もあります。
特殊な状況におけるデータも外れ値となることがあります。例えば、大規模なプロジェクトの締め切り直前期間における特定の従業員の労働時間データなどが該当します。このようなデータは、通常の業務パターンとは異なるため、外れ値として検出される可能性が高くなります。
実際に稀な事象が発生した結果として外れ値が生じることもあります。例えば、特別に高い業績を上げた従業員の生産性データなどが考えられます。このような外れ値は、組織の中で特筆すべき成果や事象を表している可能性があり、単純に無視するべきではないでしょう。
データの定義や収集方法の不一致も外れ値の原因となり得ます。異なる部署や時期のデータを統合する際に、データの定義や収集方法の違いによって、一部のデータが他から大きく外れる場合があります。例えば、ある部署では残業時間に休憩時間を含めているが、別の部署では含めていないといったとき、データを統合すると外れ値が生じます。
そもそもデータには常にさまざまな要因で生じる変動がありますが、その変動が極端に大きい人の回答が外れ値として観察されることがあります。この種の外れ値は、データの本質的な特性を反映している可能性があり、安易に除外するべきではありません。
外れ値を定義する方法の一つに、四分位範囲(IQR:Interquartile Range)を用いる方法があります。
データを小さい順に並べ、データを四等分する三つの点を見つけます。これらの点を「四分位数」と呼びます。25%の位置にある点を第1四分位数(Q1)と呼びます。全データの4分の1がこの値以下となります。50%の位置にある点を第2四分位数と呼びます。これは中央値とも呼ばれ、全データの半分がこの値以下となります。75%の位置にある点を第3四分位数(Q3)と呼びます。全データの4分の3がこの値以下となります。
四分位範囲(IQR)は、第3四分位数と第1四分位数の差として定義されます。すなわち、IQR=Q3-Q1です。この方法では、次の範囲を超えるデータを外れ値と定義します。
下限:Q1-1.5×IQRより小さい値
上限:Q3+1.5×IQRより大きい値
なお、1.5という係数は経験則に基づいており、より厳しい基準(例えば3.0)や緩い基準(例えば1.0)を用いることもあります。
例えば、ある部署の従業員50人の年間残業時間データがあるとします。このデータを小さい順に並べ、13番目のデータ(25%点)を第1四分位数、38番目のデータ(75%点)を第3四分位数とします。仮に第1四分位数が20時間、第3四分位数が50時間だったとすると、IQRは30時間(50時間-20時間)となります。
この場合、外れ値を定義する閾値は次のように計算することができます。
下側の閾値=20-1.5×30=-25時間
上側の閾値=50+1.5×30=95時間
したがって、年間残業時間が-25時間未満(現実的には0時間)または95時間を超える従業員のデータは、この定義における外れ値として扱われることになります。
外れ値がもたらす影響
外れ値の存在は、データ分析の結果に大きな影響を及ぼす可能性があります。例えば、平均値や標準偏差といった基本統計量に作用します。
平均値への影響を考えてみましょう。平均値は、全てのデータの合計をデータの個数で割ったものです[1]。式で表すと次のようになります。
平均値=(x1+x2+…+xn)/n
この式において、x1, x2, …, xnはそれぞれの値を、nはデータの総数を表します。
例えば、ある部署の10人の月額給与(万円)が次のようだったとします。
30, 32, 35, 33, 31, 34, 36, 32, 35, 200
最後の200万円が他のデータと比べて突出していますが、これを含めて平均値を計算してみましょう。
(30+32+35+33+31+34+36+32+35+200)/10=49.8
となります。しかし、この外れ値を除外して計算すると異なる結果が得られます。
(30+32+35+33+31+34+36+32+35)/9=33.1
この例から分かるように、外れ値は平均値を歪める可能性があります。
続いて、標準偏差への影響を見てみましょう。標準偏差は、データのばらつきを示す指標で、次の式で表されます[2]。
標準偏差=√[(Σ(x-x)2)/n]
この式において、Σは合計を表す記号、xは各データ値、 xは平均値、nはデータの総数です。
先ほどの給与データを使って標準偏差を計算してみると、外れ値を含む場合には、こうなります。
√[(((30-49.8)2+(32-49.8)2+…+(200-49.8)2))/10]≈52.7
他方で、外れ値を除外した場合は、こうなります。
√[(((30-33.1)2+(32-33.1)2+…+(35-33.1)2))/9]≈2.1
標準偏差にも大きな違いが生じることが分かるでしょう。
さらに、外れ値の作用は、回帰分析や相関分析といった統計手法においても顕著です。回帰分析において、外れ値は回帰直線の傾きを大きく変える可能性があります。単回帰分析の回帰直線の方程式は次のように表されます[3]。
y=ax+b
この式において、yは成果指標を、xは影響指標を表します。aは回帰直線の傾きであり、xが1単位増加したときにyがどれほど変化するかを意味します。bは切片で、x=0のときのyの値です。
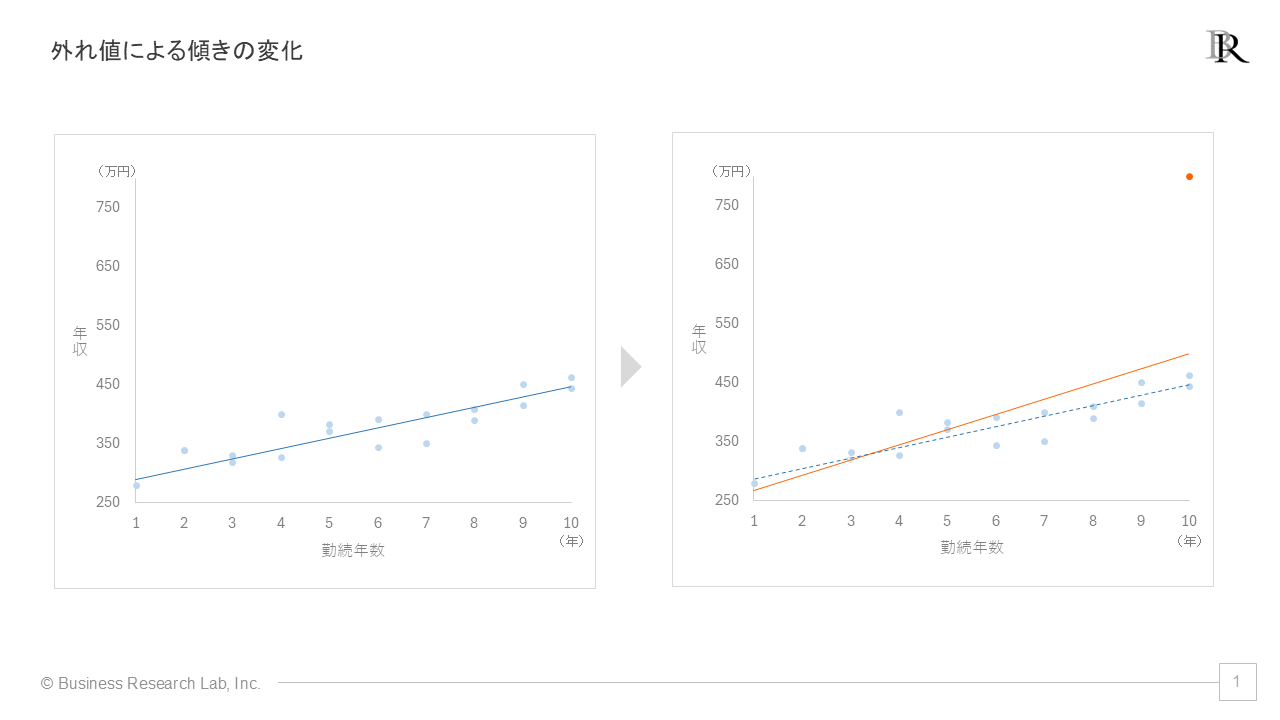
外れ値が存在すると、この傾きaが大きく変化する可能性があります。例えば、ほとんどの従業員のデータが一定の範囲内に収まっている中で、1人だけ極端に高い給与や長い勤続年数を持つデータが含まれているケースを考えてみます。
通常の従業員データだけで回帰分析を行うと、勤続年数と給与の間に緩やかな正の関係が見られるかもしれません。勤続年数が長くなるにつれて給与も少しずつ上がっていく傾向が観察されるでしょう。ここにおいて、回帰直線の傾きaは比較的小さな正の値となります。
ここに、勤続年数が長く、給与が非常に高いデータが1つ加わったとしましょう。このデータは、グラフ上で他のデータから大きく離れた位置にプロットされることになります。回帰分析では、この外れ値を含む全てのデータに最もフィットする直線を求めようとします。その結果、回帰直線は通常の従業員データの傾向から離れて外れ値に偏るように傾きが変化します。
この変化した回帰直線の傾きaは、外れ値を含まないときと比べて大きな値になる可能性が高いと言えます。勤続年数が1年増えるごとに給与が大きく上昇するような関係性が示されることになります。
しかし、この結果は実際の組織の給与体系を正確に反映しているとは言えません。大多数の従業員については、勤続年数と給与の間には緩やかな関係しかないかもしれません。それにもかかわらず、1つの外れ値によって、勤続年数と給与の間に大きな関連性があるかのような結果が導き出されてしまう可能性があるということです。
次に、相関分析においても、外れ値は相関係数に大きな影響を与えます。ピアソンの積率相関係数rは次の式で表されます[4]。
r=Σ((x-x)(y-y))/√[Σ(x-x)2×Σ(y-y)2]
この式において、xとyはそれぞれxとyの平均値を表します。xとyは分析対象の2つの指標で、Σは合計を表す記号です。相関係数は-1から1の間の値を取り、1に近いほど強い正の相関、-1に近いほど強い負の相関、0に近いほど相関が弱いことを指します。
外れ値が存在すると、この相関係数が実態とは異なる値を示す可能性があります。例えば、先ほど示した散布図と同様に、ほとんどの従業員のデータでは勤続年数と給与に正の相関があるとします。勤続年数が長くなるにつれて給与も上昇していく対応関係が大まかに見られるということです。
ここに、勤続年数は短いが極端に高給の従業員のデータ(例えば、高度なスキルを持つ新規採用者)が含まれたケースを考えてみましょう。このデータは、他の従業員データの傾向とは大きく異なります。具体的には、x軸(勤続年数)の値が小さいにもかかわらず、y軸(給与)の値が非常に大きいデータとしてプロットされます。
このような外れ値が存在すると、全体の相関係数が低下してしまいます。なぜなら、この外れ値は全体の傾向とは逆の関係(短い勤続年数で高給)を示しているからです。
このように、外れ値の存在によって相関分析の結果が歪められてしまいます。そのため、相関分析を行う際にも、外れ値の有無とその影響を慎重に検討しなければなりません。
外れ値の検出
外れ値を適切に扱うためには、まずそれを検出する必要があります。外れ値の検出方法には様々なアプローチがありますが、ここでは主に統計的手法と可視化技法を紹介します[5]。
統計的手法
Zスコア
各データを標準化し、その値が一定の閾値を超えるものを外れ値として検出する簡便な方法のひとつです[6]。Zスコアは次の式で導き出すことが可能です。
Z=(x-x)/σ
この式において、xは各データの値を表します。xはデータセット全体の平均値で、σは標準偏差です。
Zスコアは、各データが平均からどれほど離れているかを、標準偏差を単位として表現したものです。例えば、Zスコアが2であれば、そのデータは平均から標準偏差の2倍離れていることを意味します。
一般的に、|Z|>3を外れ値の基準とすることが多いと言えます。正規分布を仮定した場合、データの99.7%が平均から標準偏差の3倍以内に収まるという規則に基づいています。しかし、より厳しい|Z|>4や緩い|Z|>2.5などの基準を用いることもあります。
例えば、ある部署の従業員の年間残業時間が次のとおりだったとします[7]。
20, 25, 30, 28, 35, 22, 40, 200
平均μと標準偏差σを計算しましょう。
μ=(20+25+30+28+35+22+40+200)/8=50
σ=√[((20-50)2+(25-50)2+(30-50)2+(28-50)2+(35-50)2+(22-50)2+(40-50)2+(200-50)2)/8]≈58.69
各データのZスコアを算出します。
20:(20-50)/58.69≈-0.51
25:(25-50)/58.69≈-0.43
30:(30-50)/58.69≈-0.34
28:(28-50)/58.69≈-0.37
35:(35-50)/58.69≈-0.26
22:(22-50)/58.69≈-0.48
40:(40-50)/58.69≈-0.17
200:(200-50)/58.69≈2.56
この場合、|Z|>2.5の基準を用いると、200時間のデータが外れ値として検出されます。
四分位範囲
先に説明した四分位範囲を用いる方法も、外れ値の検出に用いられています。この方法では、データを順に並べ、25%点(Q1)と75%点(Q3)を求め、その差(IQR)を計算します。そして、[Q1-1.5×IQR, Q3+1.5×IQR]の範囲外にあるデータを外れ値とみなします。
先ほどの年間残業時間のデータを使って具体的に計算してみましょう。
20, 25, 30, 28, 35, 22, 40, 200
Q1(25%点)=24.75
Q3(75%点)=36.25
Q1とQ3の値は、データを小さい順に並べた時の下位25%と上位25%の境界値を意味します。この例では、データ数が8個で偶数のため、25%点と75%点は実際のデータ値の間に位置します。そのため、Q1は2番目と3番目のデータの平均((22+25)/2=24.75)、Q3は6番目と7番目のデータの平均((35+40)/2=37.5)として算出しています。
IQR=36.25-24.75=11.5
下限=24.75-1.5×11.5=7.5
上限=37.5+1.5×11.5=53.5
年間残業時間が7.5時間未満または53.5時間超のデータが外れ値となり、この場合200時間のデータが外れ値として検出されます。
可視化技法
箱ひげ図
箱ひげ図は、データの分布と外れ値を視覚的に表現する方法となります[8]。箱の下端がQ1、上端がQ3を表し、箱の中の線が中央値を示します。箱から伸びるヒゲの長さは通常1.5×IQRで、このヒゲを超えるデータが外れ値として表示されます。
ヒストグラム
ヒストグラムを用いると、データの分布を視覚化でき、他のデータから離れた位置にあるバーが外れ値である可能性があります。
散布図
2つの指標の関係を見る際には散布図が有用です。他のデータから明らかに離れた位置にプロットされるデータが外れ値の候補となります。
外れ値への対処
外れ値を検出した後、それにどのように対処するかは分析の目的や状況によって異なりますが、いくつかの対処方法を挙げておきましょう。
保持
外れ値が正当なデータであり、重要な情報を含んでいる場合は、そのまま保持します。例えば、高業績社員の突出したパフォーマンスデータなどは、組織の特性を理解する上で重要な情報となるかもしれません。その場合、もし外れ値により回帰分析や相関分析の結果が偏って見えても、それは実態を表した結果だといえます。
この方法を選択する際は、データの正確性を確認することが大事です。外れ値が実態を正確に反映しているかを慎重に検証する必要があります。また、そのデータが分析や意思決定にとって重要な情報を含んでいるかを評価することも必要です。
外れ値を含めることで、全体的な分析結果にどのような影響があるかを考え、より適切な分析手法に切り替えたり後述のロバストな推定値を用いるなど判断しましょう。
除外
明らかなエラーや、分析の目的に適さないデータである場合は、除外することが適切な場合もあります。ただし、除外する際はその理由を記録し、透明性を確保しましょう。
除外を検討する際は、まずそのデータが明らかな誤りや測定ミスによるものかを確認します。例えば、給与データで桁が明らかに間違っている場合などが該当します。
次に、そのデータが現在の分析目的に関連しているかを評価します。例えば、無期雇用の社員の給与分析を行う際に有期雇用の社員のデータが混入している場合などは、分析目的との整合性がないため除外を検討します。
そのデータを除外することで、分析結果がどのように変化するかを検討することも大切です。結果が大きく変わる場合は、その影響を慎重に評価します。
変換
データの分布を正規分布に近づけるために、対数変換や平方根変換などの方法を用いることがあります。例えば、給与データなどの右に裾の長い分布では、対数変換を適用することで外れ値の影響を軽減できる場合があります。
変換を行う際には、どのような変換がデータの性質に適しているかを吟味します。例えば、給与データや売上データなど、正の値をとるデータには対数変換が適している場合があります。そして、変換後のデータが元の文脈でどのように解釈できるかを考慮します。例えば、対数変換を行った場合、結果は「給与の対数値」となるため、その解釈には注意が必要です。
分析後に結果を元のスケールに戻す必要がある場合、逆変換の方法も考慮に入れると良いでしょう。分析結果を元の単位で解釈することができます。
ロバストな統計手法
外れ値の影響を受けにくいロバスト(頑健)な統計手法を選択することも一つの方法です。例えば、平均の代わりに中央値を使用したり、ピアソンの相関係数の代わりにスピアマンの順位相関係数を使用したりすることで、外れ値の影響を軽減できます。
ロバストな統計手法を使用する際は、初めに、どの統計手法が分析の目的とデータの性質に適しているかを検討します。続いて、ロバストな統計手法を使用した場合、結果の解釈が従来の方法と異なる可能性があることを理解し、適切に説明できるようにします。
一部の統計手法は、小さなサンプルサイズでは精度が低下する可能性があります。データ量に応じて手法を選択しなければなりません。
外れ値への対処方法によって分析結果が大きく変わる可能性がある場合は、複数のアプローチを試み、結果の安定性を確認することが推奨されます。
いずれにせよ、外れ値の存在自体が重要な情報を持っている可能性があることを忘れてはいけません。例えば、特定の部署や職種で外れ値が頻繁に発生する場合、そこに何らかの構造的な問題や特殊な状況が存在する可能性があります。こうした場合、外れ値を単に統計的な問題として扱うのではなく、組織の改善につながる手がかりとして捉えることができるでしょう。
脚注
[1] 平均値を含む代表値の詳細については当社コラムを参考にしてください。
[2] 標準偏差を含む散布度の詳細については当社コラムをご確認いただければと思います。
[4] 相関係数について詳しく知りたい場合は当社コラムをご一読ください。
[5] 本コラムでは主に単変量解析における外れ値の扱いに焦点を当てていますが、人事データ分析では多変量解析を行うこともあります。多変量解析における外れ値の検出や処理には、単変量解析とは異なるアプローチが必要です。例えば、マハラノビス距離を用いた方法があります。これは、各データと多変量空間の中心との距離を、共分散行列を考慮して計算する方法です。他にも、主成分分析やクラスター分析などの手法を用いて、多次元空間での外れ値を特定することも可能です。多変量解析における外れ値は、単一の変数では検出できない複雑な関係性を示すことがあるため、より慎重な解釈が求められます。
[6] この方法は簡便でよく用いられますが、外れ値の検出に用いる平均と標準偏差の値が外れ値によって偏るため、統計的に厳密な判断にならない欠点があります。また、Zスコアを用いた外れ値の検出は、データが正規分布に従うことを仮定しています。しかし、場合によっては、この前提を満たさないことがあります。例えば、給与データは右に歪んだ分布を示すことがあり、そのようなケースは、Zスコアによる外れ値の検出は適切でない可能性があります。データの分布を確認し、必要に応じて他の方法を検討しましょう。
[7] この例は、外れ値の影響を理解しやすくするために、意図的に小さなデータセットを使用しています。実際の分析では、より大きなデータセットを扱うことが多く、その場合、単一の外れ値が平均や標準偏差に与える影響は小さくなります。そのため、200時間のデータのZスコアは、より大きな値(例えば4以上)となる可能性が高くなります。この例の限界を理解しつつ、外れ値の概念把握にご活用ください。
[8] 箱ひげ図やヒストグラムなどの可視化技法は外れ値の検出に有用ですが、これらの方法にも限界があります。例えば、大規模なデータセットにおいては、箱ひげ図が多数の外れ値を示す可能性があり、その解釈が難しくなる場合があります。また、ヒストグラムではビンの幅の選択によって外れ値の見え方が変わることがあります。可視化技法を用いる際は、これらの限界を理解し、複数の手法を組み合わせて総合的に判断することが重要です。
執筆者
 伊達 洋駆 株式会社ビジネスリサーチラボ 代表取締役
伊達 洋駆 株式会社ビジネスリサーチラボ 代表取締役
神戸大学大学院経営学研究科 博士前期課程修了。修士(経営学)。2009年にLLPビジネスリサーチラボ、2011年に株式会社ビジネスリサーチラボを創業。以降、組織・人事領域を中心に、民間企業を対象にした調査・コンサルティング事業を展開。研究知と実践知の両方を活用した「アカデミックリサーチ」をコンセプトに、組織サーベイや人事データ分析のサービスを提供している。著書に『60分でわかる!心理的安全性 超入門』(技術評論社)や『現場でよくある課題への処方箋 人と組織の行動科学』(すばる舎)、『越境学習入門 組織を強くする「冒険人材」の育て方』(共著;日本能率協会マネジメントセンター)などがある。2022年に「日本の人事部 HRアワード2022」書籍部門 最優秀賞を受賞。東京大学大学院情報学環 特任研究員を兼務。