近年、実務の領域には様々な統計解析が導入され始めています。そうしたなか、最も慣れ親しんでいるものの1つが代表値です。例えば、会社の年間業績の推移や組織サーベイ・適性検査の結果として、まず平均点や得点の分布を確認することが多いでしょう。

高度な統計解析を扱えることは素晴らしいことですが、こうした基礎的な指標から、データの特徴をきちんと把握できることも重要です。本コラムでは、記述統計としての代表値を取り上げ、実際に公表されているデータを題材に、その特徴や利点、解釈上の注意点を取り上げていきます。

代表値とは

今回取り上げる代表値とは、測定した項目・指標のデータについて、全体的な分布の特徴を1つの値で表すために使われる指標の総称です^[1]。

測定したデータには、個々の項目や指標に対して、回答者の人数分だけ入力された値があります。数十～数百と人数分並ぶひとつひとつの値を見渡しても、その特徴はよくわかりません。その特徴を1つの値で示したものが代表値です。

そのため、代表値の意味を理解することで、データを正確に捉えることにつながります。以降では、実務家の集計に役立つ3つの代表値を、距離に関する話題と使用例に触れながら、詳しく見ていきます。

集計に役立つ有名な代表値；平均・中央値・最頻値

代表値には様々な種類があるなかで、どの代表値を用いるのが良いでしょうか。それは、どのような測定内容のデータであるか、あるいは、どのような分析に用いるかなど、データの特徴や分析目的によっても、どの代表値を用いると良いのかが変わります。

有名な代表値としてまず挙げられるのが「平均」です。これは、ある指標における全データの値を足し合わせ、その合計をデータの個数で割ったものです。実務に関わるデータの多くで平均が示されており^[2]、代表値の中でも最も一般的な指標といえるでしょう。算出方法も簡単なことから、代表値として使用頻度が多い事もうなずけます。

次に「中央値」を紹介します。これは、データ全体の最も大きな値から小さな値へと並べたとき、その順位が真ん中になる値です。例えば、国内外の年収や賃金の調査結果などで、平均とあわせて中央値が報告されます^[3]。

詳細は後述しますが、平均はデータ全体に含まれる外れ値の影響を受けやすく、それによって実態に即していない偏った値が算出されてしまうケースがあります。そのため、中央値をあわせて確認することで、データ内で中心的な位置にある値を確認することができるというメリットがあります。

最後に「最頻値」です。これは文字通り、データ全体の中で、最も頻繁に現れる値です。例えば、購買データの中で最も多く売れたものを確認したり、投票で最も多い得票数を得た人・商品・選択肢を採用するといった具合で使用されることが多いでしょう。

3つの指標が正確なデータの把握につながる

上記の3指標がよく使われる理由として、これらを同時に確認することにより、データ全体に含まれる値がどう偏っているか推測でき、データの特徴をより正確に把握できることがあります。具体的には、次の3つのパターンを想定することができます。

一つ目は、データ全体に、大きな値が比較的多く含まれているパターンです。たとえば、100人が適性検査を受けたとして、ほとんどの受検者が100点から70点の高得点圏に集中し、その他の受検者は70点未満の得点圏に数名ずついるような状態だとします。このとき、上記の3指標は、平均＜中央値＜最頻値の関係になることが知られています。

3つの指標がこのような関係性になる理由として、まず「大きな値が多い」ということは、最頻値と中央値が「値の個数」に準じて決まるため、大きな値になると想定できます。それに対して平均は、データ全体に含まれる全ての値、つまり、比較的小さな値を含めた計算によって算出されるので、3つの指標の中では最も小さくなりやすいのです。

二つ目のパターンは、上記とは逆に、データ全体に小さな値が比較的多く含まれるパターンです。例えば、大企業の従業員を勤続年数によって一覧したとき、多くは数年～10年以内に含まれるのに対して、10年を超え、20年や30年勤める従業員も少しずつ在籍しているという具合です。このときの関係性は、最頻値＜中央値＜平均になります。理由も上記と逆に、小さな値の個数によって最頻値と中央値が小さくなり、比較的大きな値も含めて計算される平均が大きくなるのです。

三つ目のパターンは、大きな値も小さな値も、同程度に含まれている場合です。この時、3つの値は、同じ値をとることが多いとされています。実際に人間が答えたデータを扱う場合、様々な影響から全く同じにはなりえません。とはいえ、ほぼ同じ値をとることで、この傾向にあるとみなすことができます。

以上をまとめると、3つの代表値の関係から、データ全体の特徴を次のように確認することができます。

• 平均＜中央値＜最頻値 →大きな値が多く含まれて偏っている
• 最頻値＜中央値＜平均 →小さな値が多く含まれて偏っている
• 3つの代表値がほぼ同値 →大きな値と小さな値が同程度に含まれて偏っていない

このように、3つの代表値を確認することで、データ全体の特徴を大まかに把握することが可能です。

活用の具体例

参照する調査の概要；日本国民の所得金額

ここからは、実際に報告されているデータを確認することで、代表値に沿ってデータ全体の特徴を解釈することの重要性を確認していきます。確認する例は、厚生労働省により実施された2023年「国民生活基礎調査」の調査結果^[4]です。

この調査は、国民生活の基礎的な事項（保健、医療、福祉、年金、所得など）を調査することで、厚生労働行政の企画・立案に必要な資料を得ることが目的とされています。2023年は、全国の約6万1千世帯とその構成員約13万6千人を対象に、世帯の基本情報や所得についての調査が行われています。

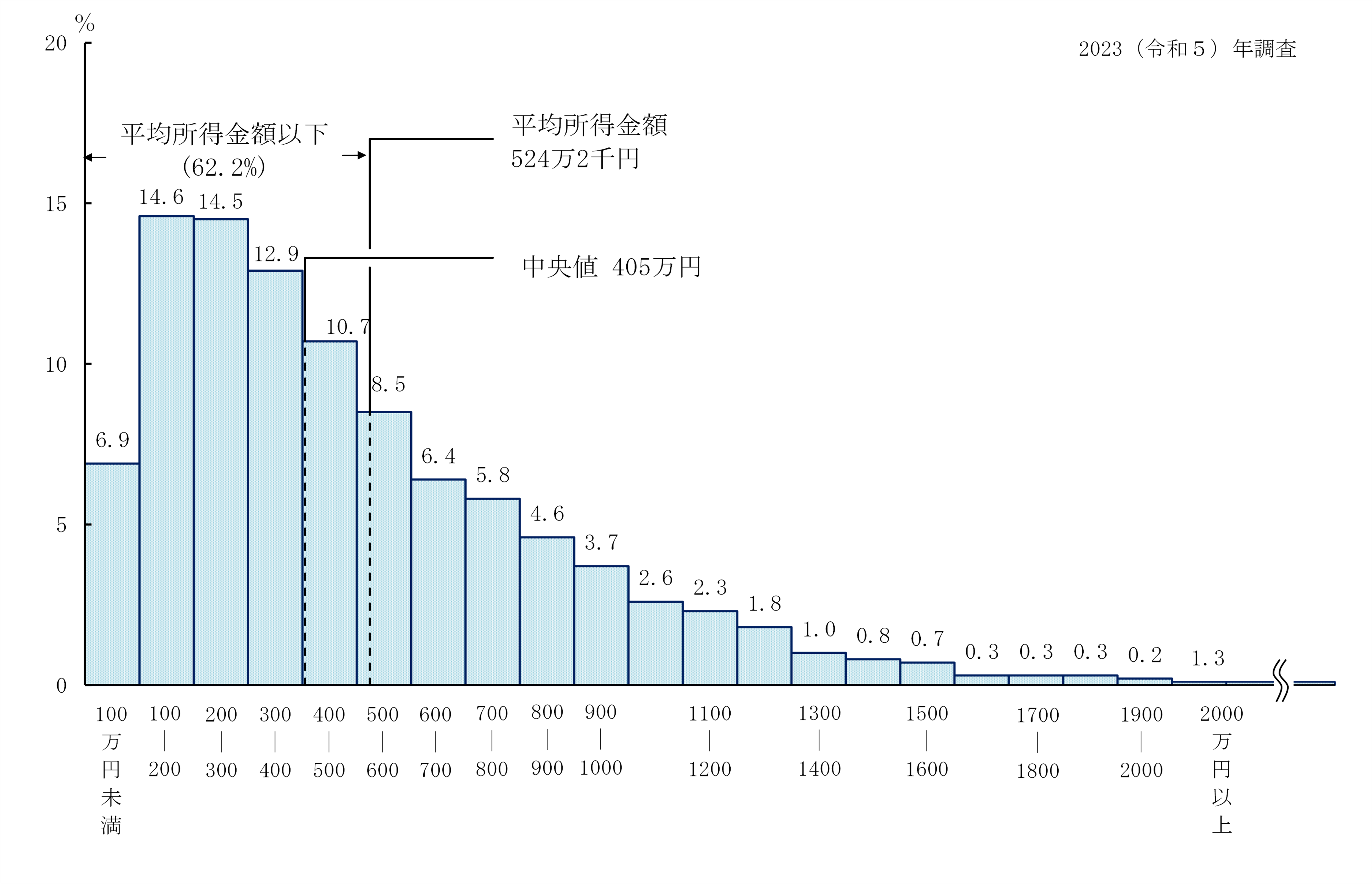
その調査の中から、本コラムと関連の強い内容として、所得金額の階級別に確認した「所得の分布状況」の結果を確認します。具体的な調査結果は、以下の図^[5]のようになっています。

この図では、横軸には、回答者が100万円単位で群分けされ、縦軸には、各群の比率が示されています。また、所得の平均は524.2万円、中央値は405万円であり、所得が平均を下回っている層の割合が62.2％であることも、あわせて報告されています。最頻値については、明確な金額が確認できないものの、回答者の比率として「100～200万円（14.6%）」「200～300万円（14.5％）」の層が、相対的に多いことを参照できます。

平均のみを判断基準にするリスク

こうした調査結果が得られたとき、平均のみを確認することで実態を把握した判断する場合が多いと予想されます。しかし、平均は外れ値に弱い特徴があり、データ全体の特徴を適切に表せていない可能性があることは上述の通りです。そこで、上記の調査結果に対して、仮に平均のみを参考に施策の意思決定を行った場合のリスクを考えてみます。

先に、中央値の結果を参考にすると、回答者の半数は、405万円以下の所得で生活していることが確認できます。しかし、平均のみにより「回答者の大体の年収が524.2万円」と解釈した場合、100万円以上の誤差を伴っていることになります。

このことは、例えば、交付金を支給するうえで、支援が必要な世帯や適切な支給額を誤って判断するリスクにつながります。逆に、平均以上の所得を得ている世帯から支援の必要性に対する理解を得られず、施策に不公平感を生じてしまう可能性もあるでしょう。

代表値によってデータの特徴を読み取る

こうした点を踏まえつつ、3つの代表値に注目することで、実態をより正確に読み取れる事を確認していきます。先ほどの所得データの代表値は、最頻値、中央値、そして平均の順に、所得の値が高くなっています。このことから、「比較的所得の低い回答者がデータ全体を占めているのだろう」ということが、先ほどのように視覚化された結果^[6]がなくとも把握できます。

また、この傾向からは、この調査の平均が、所得の高い回答者によって押し上げられていることもわかります。例えば、「2000万円以上（1.3％）」の所得を得ている層などが、平均に影響を及ぼしていると考えられます。最頻値が100万円～300万円の範囲にあり、中央値と平均値に100万円以上の差があることも併せて確認することで、実態をより正確にとらえることができます。細かいデータによる確認は必要ですが、例えば、所得の高い回答者を施策でどこまで考慮するべきかといった意思決定にも活かせるでしょう。

活用時のコツ

多角的な視点を持つ

最後に、代表値によってデータを確認する際のポイントをまとめていきます。ここでは、報告されているデータを読む場合と、自らデータを分析・報告する場合に分けて考えていきます。

初めに、代表値の特定の指標のみを参考にするのではなく、複数の指標を取り扱う姿勢を持つことが大切です。

データを読む立場では、上記の例のように、平均のみを参考にした場合に、データ全体の傾向を誤解するリスクがあります。調査結果として、平均、中央値、最頻値など、複数の指標が報告されている場合もありますが、平均のみが報告されているものも少なくありません。もし重要な意思決定に関わるデータであれば、そのソースが社内・社外を問わず、出来る限り指標を確認するべきです。

逆に、自らデータを分析・報告する場合は、積極的に複数の指標を報告することで、データの読み手に、潤沢な情報提供ができます。それぞれの代表値が異なる意味を持つ指標であることは勿論、それらの関係性を考慮することで見えるデータ全体の特徴を正確に伝えるためにも、各指標の報告が重要です。

外れ値を考慮する

二つ目のポイントは、データ全体に外れ値が含まれているかを確認することです。外れ値とは、データ全体に含まれる他の値よりも、極端大きい、または、極端に小さな値のことです^[7]。外れ値は、上記3つの代表値のうちでは、特に平均に大きな影響を与えます。例えば、極端に大きな値が含まれている場合は平均が大きくなり、極端に小さな値が含まれている場合は、逆に小さな値になります。

今後は、データを分析する立場のポイントから見ていきます。データ分析の際は、扱っているデータに外れ値が含まれているかどうかを確認しましょう。もし外れ値が含まれていると、データ全体の特徴を読み違える事に留まらず、その後の高度な分析の結果や、分析結果に基づく打ち手の有効性にも影響が及ぶ可能性があります。代表値は「外れ値の影響を受けた後」の値になっている場合があるので、実際に元データ（ローデータ）を確認することが重要です。

一方、データを読む立場では、多くの場合でローデータを入手することができないので、外れ値によるデータの誤解を完全に防ぐことは難しいといえます。しかし、幾つかの観点をあわせて確認するように心がけると、誤解するリスクを抑えることができます。

まずは、中央値を確認することです。中央値は外れ値の影響が少ないことが分かっています。このことから、平均だけでなく、外れ値の影響を受けにくい中央値をあわせて確認することが重要です。

次に、データ全体が、どのような内容を測定しているのかを考慮することです。たとえば、特定のスキルや認知機能といった能力を測定している場合、極端に優秀な成績を示す参加者が含まれることがあり得ます。このように、もし外れ値が含まれそうな測定内容であれば、データの読み取りに特に注意することが必要だといえます。

最後に、サンプルサイズを確認することです。もしサンプルサイズが小さい場合、外れ値でない通常のデータの個数が少ないことになり、影響が強く現れます。たとえば、国家単位の大規模調査を参考にする場合は、そこまで注意する必要はないでしょう。一方で、組織サーベイやフィールド実験のように、数百あるいは数十人といった規模でのデータを読む際は、外れ値による影響を考慮しながら、データを確認するのが良いでしょう。

脚注

^[1] 本章の解説は、以下の書籍に基づいています；南風原 朝和（2002）. 心理統計学の基礎 総合的理解のために（有斐閣アルマ）　pp17-41

^[2] 専門的には、上記の方法で算出される値は「算術平均」と呼ばれます。算術平均の他にも、用いる値や計算式が異なる平均も存在します。詳細は以下のサイト等をご確認ください；Bell curve 「統計WEB いろいろな平均」（2024.9.12参照）（https://bellcurve.jp/statistics/course/4324.html?srsltid=AfmBOoo8ftaZKdUXe6jd1rlxlH0ic-wcEZIPQiUwvX-X5EGKUHsWaiQo）

^[3] 例えば、経済開発協力機構（OECD）のオープンデータから、各国の年収や最低賃金の推移などにおいて、中央値が報告されている事を確認できます。詳細は以下サイトを参照ください；OECD Data Explorer（https://stats.oecd.org/）

^[4] 詳細は、以下を参照ください；厚生労働省「2023（令和５）年　国民生活基礎調査の概況」（2024年9月3日に確認）（https://www.mhlw.go.jp/toukei/saikin/hw/k-tyosa/k-tyosa23/index.html）

^[5] 「2023（令和５）年　国民生活基礎調査の概況」に関する図表として、以下のリンクより参照しています（2024年9月3日に利用）；所得に関する図表・xlsx形式（https://www.mhlw.go.jp/toukei/saikin/hw/k-tyosa/k-tyosa23/xlsx/07.xlsx）

^[6] 上記の図はヒストグラムと呼ばれ、回答をいくつかの水準に分けたうえで、各水準に該当する回答者数が何名であるのかを集計したものです。データ自体が手元にある場合は、各種のソフトウェアを利用することで比較的簡単に算出することができるので、代表値に加えて確認すると良いでしょう。

^[7] ただし、どの程度の違いがある場合に外れ値とみなすべきかどうかについては、議論の余地があります。データ分析を行う場合は、恣意的な理由で削除しないことや、どのような基準で削除したのかを明記しておくことが重要です。