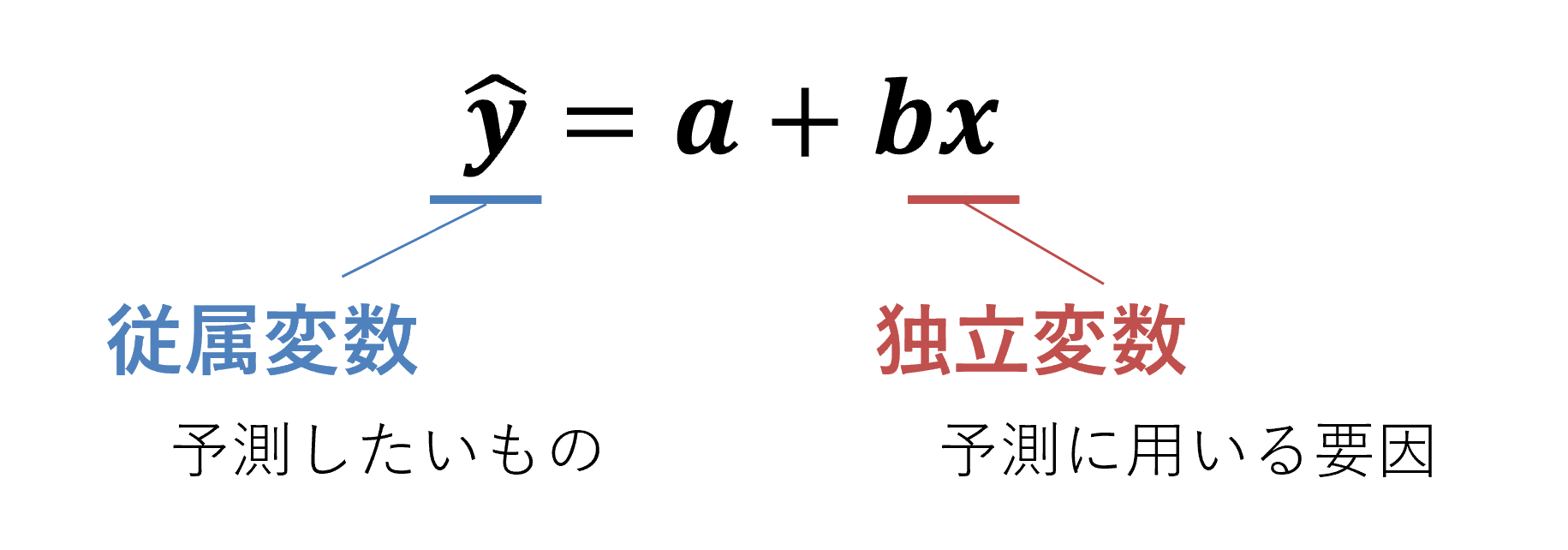※本コラムは、2021年2月に開催したセミナー「人事のためのデータ分析入門：回帰分析～要因を見出すための分析～」の内容をもとに加筆・再構成したものです。

回帰分析にできること

①要因が分かる

本コラムのテーマは回帰分析、特に重回帰分析というデータ解析手法です。はじめに、回帰分析・重回帰分析で分かること・できることを説明します。

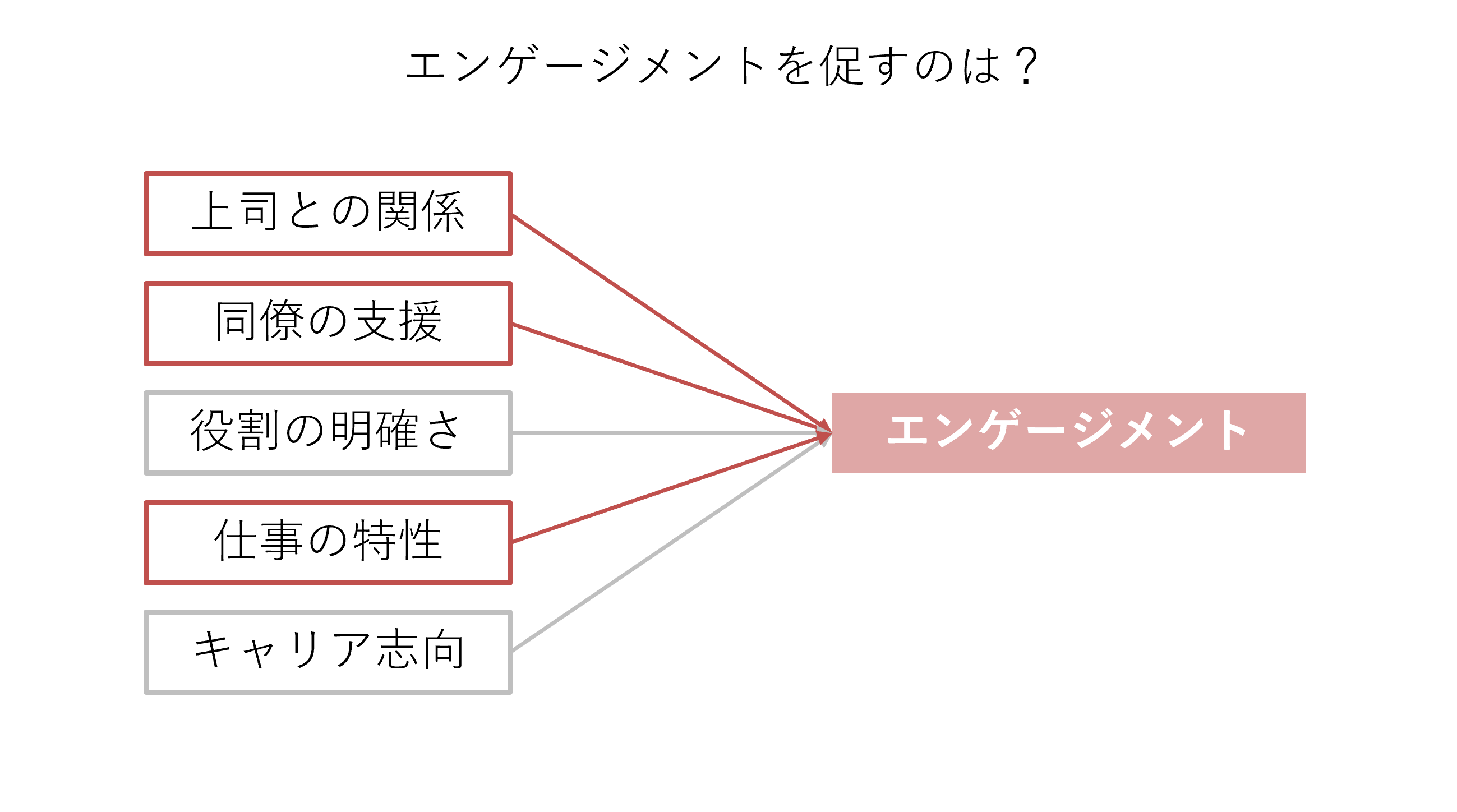
一つは、「関心のある物事の要因が何か」が分かります。例えば「従業員たちのエンゲージメントを促すものは何か知りたい」と考えているとします。従業員のエンゲージメントと、それを促す要因の候補についてデータを取得し、重回帰分析をすれば、何がエンゲージメントを促す要因かを判断できます。例えば下図のような分析結果を得られれば、「『上司との関係』『同僚の支援』『仕事の特性』がエンゲージメントを高める」と言えます。

 

②要因の重要度を比較できる

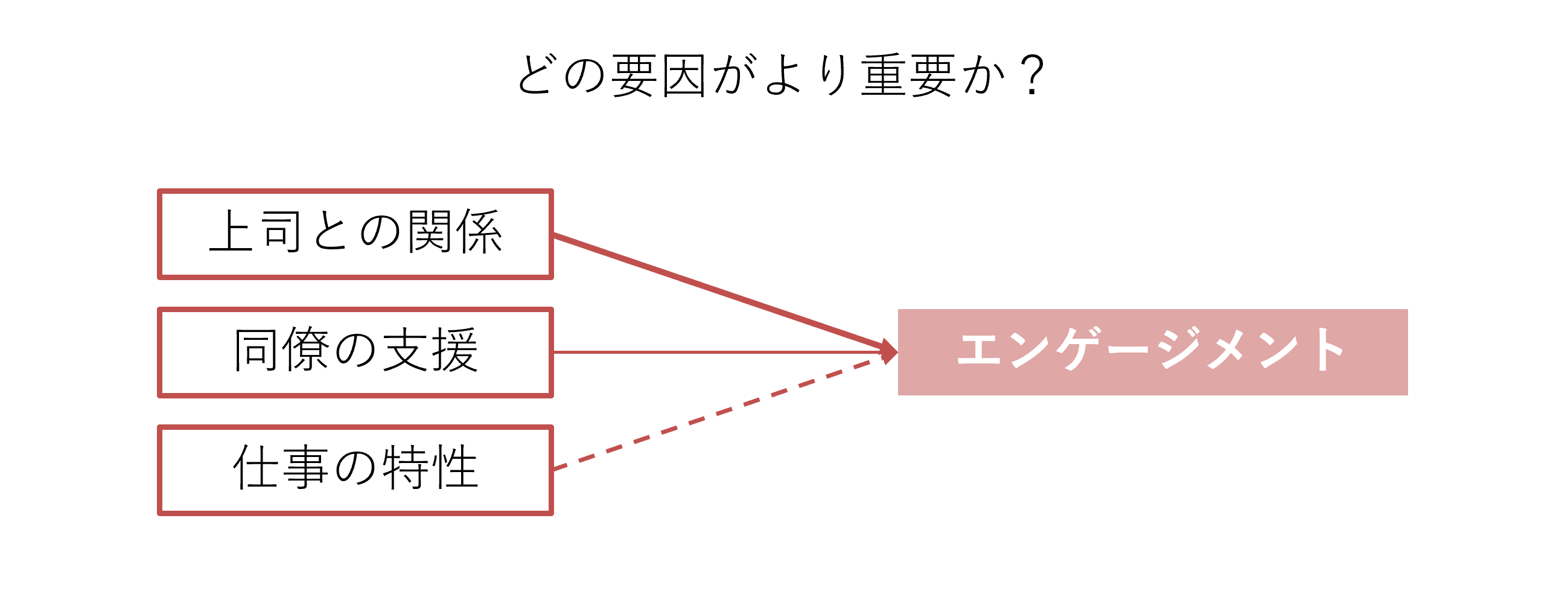
もう一つは、それぞれの要因の重要度（影響度）を比較できます。先の例では「上司との関係」「同僚の支援」「仕事の特性」がエンゲージメントを促すと分かりました。この3つのうち、どの要因がより重要かが、重回帰分析によって把握できます。例えば下図のイメージで、「特に重要なのは『上司との関係』」ということが重回帰分析の結果から理解できます。

 

１．回帰分析の基本的な考え方

回帰分析・重回帰分析でできることについて紹介しました。続いて、回帰分析の基本的な考え方を説明します。

2つのデータから描く散布図

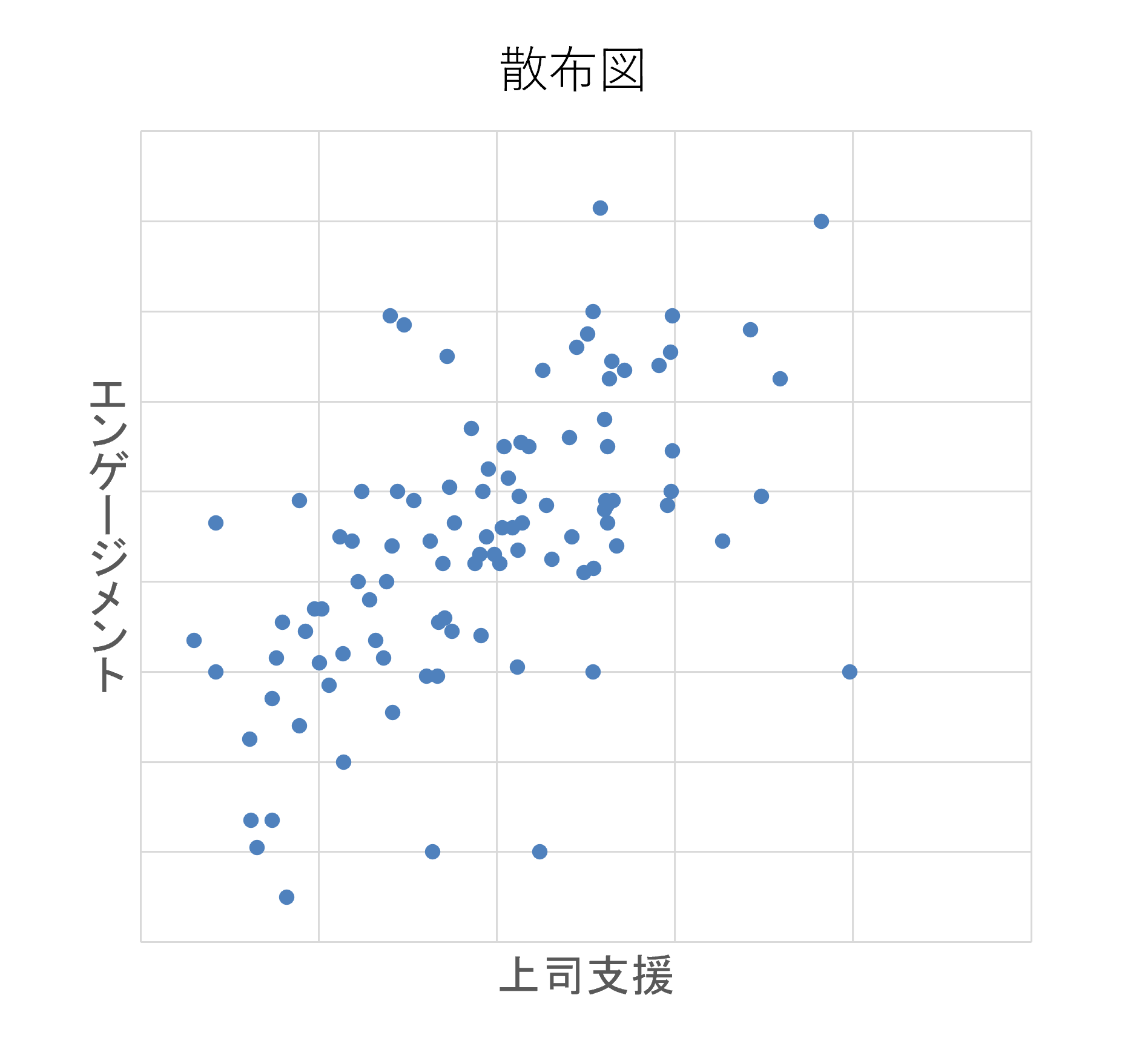
例えば、社内で組織サーベイを実施し、「エンゲージメント」と「上司からの支援（部下が上司から支援を得られている程度）」の2つを測定したとします。2つのデータを組み合わせて、縦軸をエンゲージメントの値、横軸を上司からの支援の値にした「散布図」を描くことができます（下図参照）。

上の散布図を見てください。点が散らばっています。この散らばりを見て、エンゲージメントと上司からの支援の関連について、一言で表現できるでしょうか。なかなか難しいと思います。この難しさを克服し、複数のデータの関係を統計学的に表現しようとするのが、回帰分析です。

残差が小さくなるように求める回帰直線

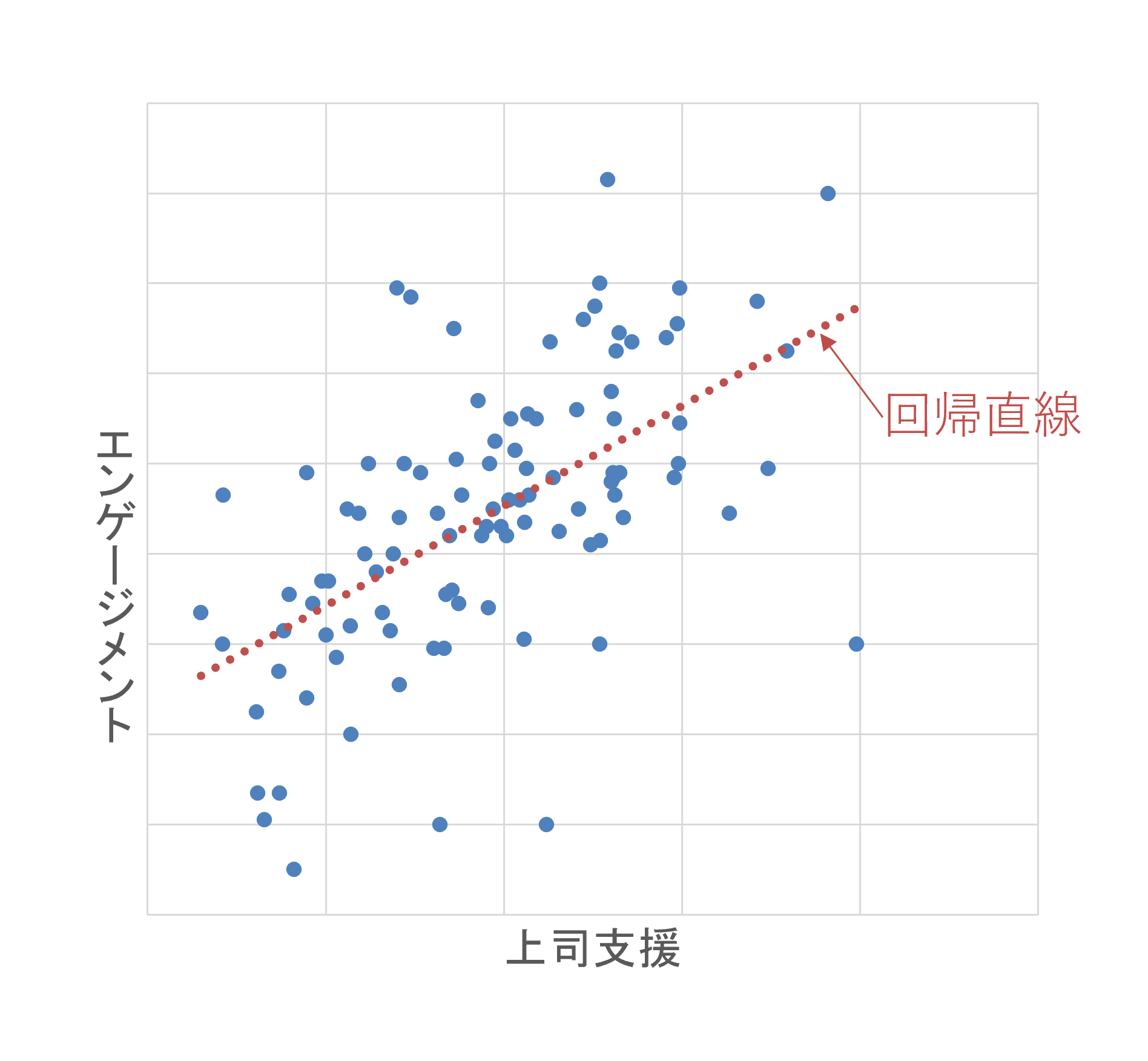
「回帰」とは、散布図のデータ（それぞれの点）を、1本の線に集約させることを意味します。散布図全体の様子を捉え、データの散らばりをうまく説明するように線を引きます。下図でいえば、点線がそれに当たります。この線のことを回帰直線と呼びます。回帰分析では、回帰直線を統計学的に求めます。

ここでひとつ疑問が浮かぶかもしれません。「データの散らばりをうまく説明する直線をどのように決めればよいのか」という疑問です。この疑問に答える上で重要になるのは、「残差」です。

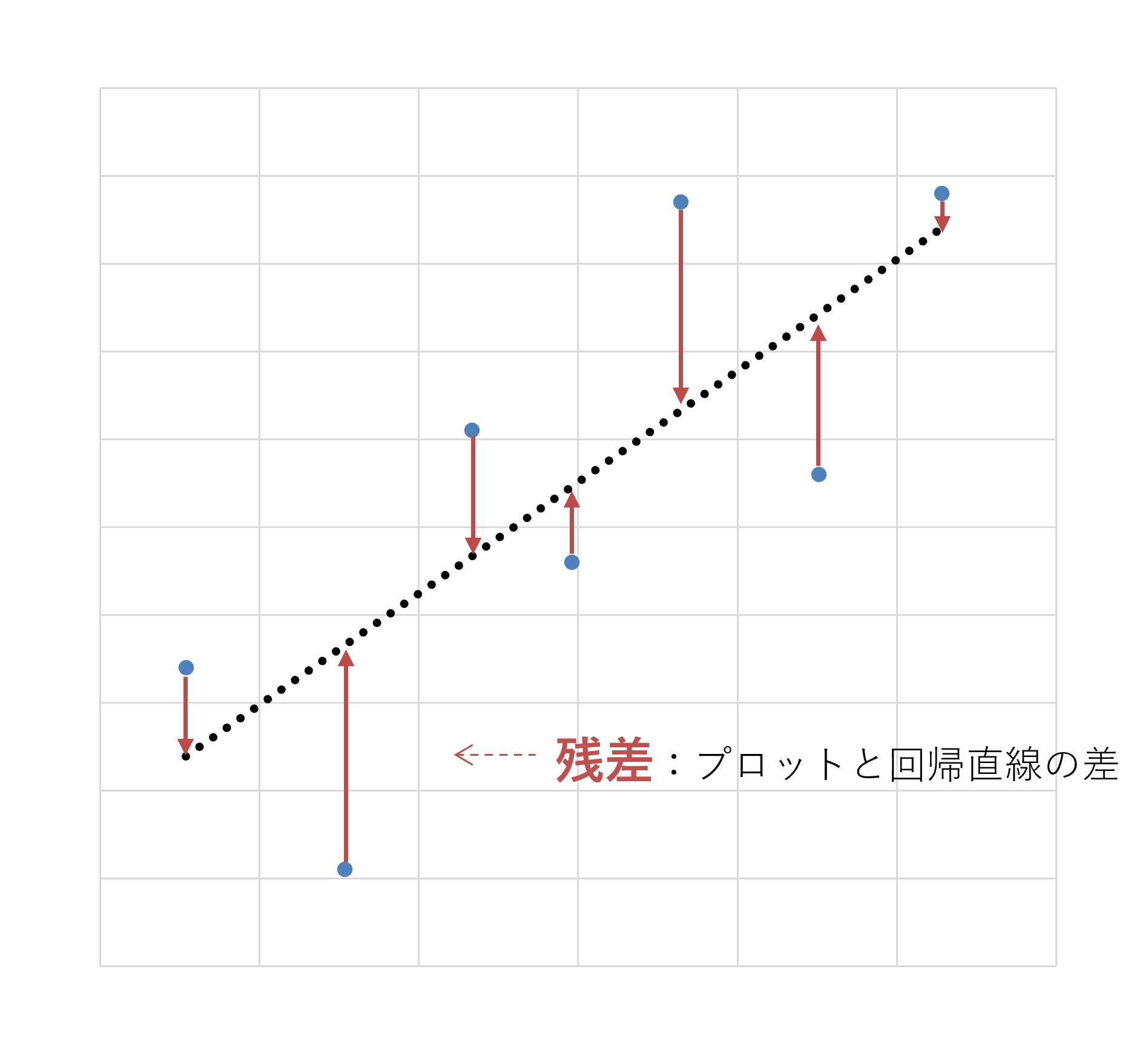
残差とは、下図の赤い矢印で表されるものです。散布図において、測定された各データの点（プロット）と回帰直線が離れている程度、すなわち、それぞれのプロットと回帰直線の差を指します。

回帰直線を決めるためには、各残差の合計を可能な限り小さくする必要があります。残差の合計が大きくなればなるほど、その直線は実際のデータからかけ離れていることになるからです。

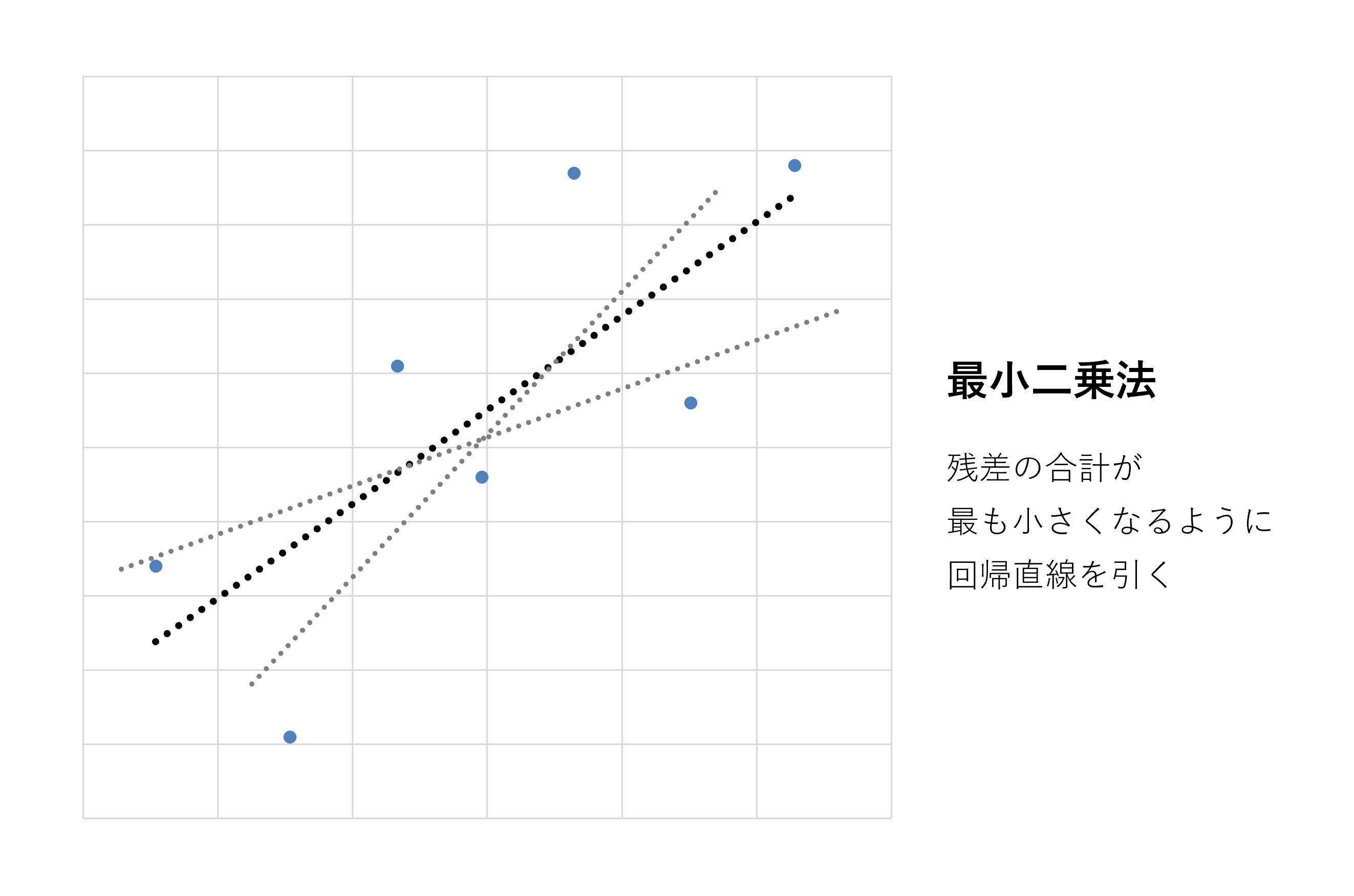
回帰分析では残差の合計が最も小さくなるように回帰直線を求めます。この方法は「最小二乗法」と呼ばれています[1]。最小二乗法を用いることで、実際のデータとのずれが最も小さい直線を決めることができます。

---

 

２．回帰直線の求め方

回帰分析の概念的な紹介を終えました。では、回帰直線の具体的な計算方法について説明します。

回帰直線の式、回帰式

x、yという2つの値を測定した場合を想定します。yは「関心のある物事」で、先の例では「エンゲージメント」に当たります。xは「関心のある物事に影響する要因（影響要因）」で、先の例では「上司からの支援」に当たります。

 

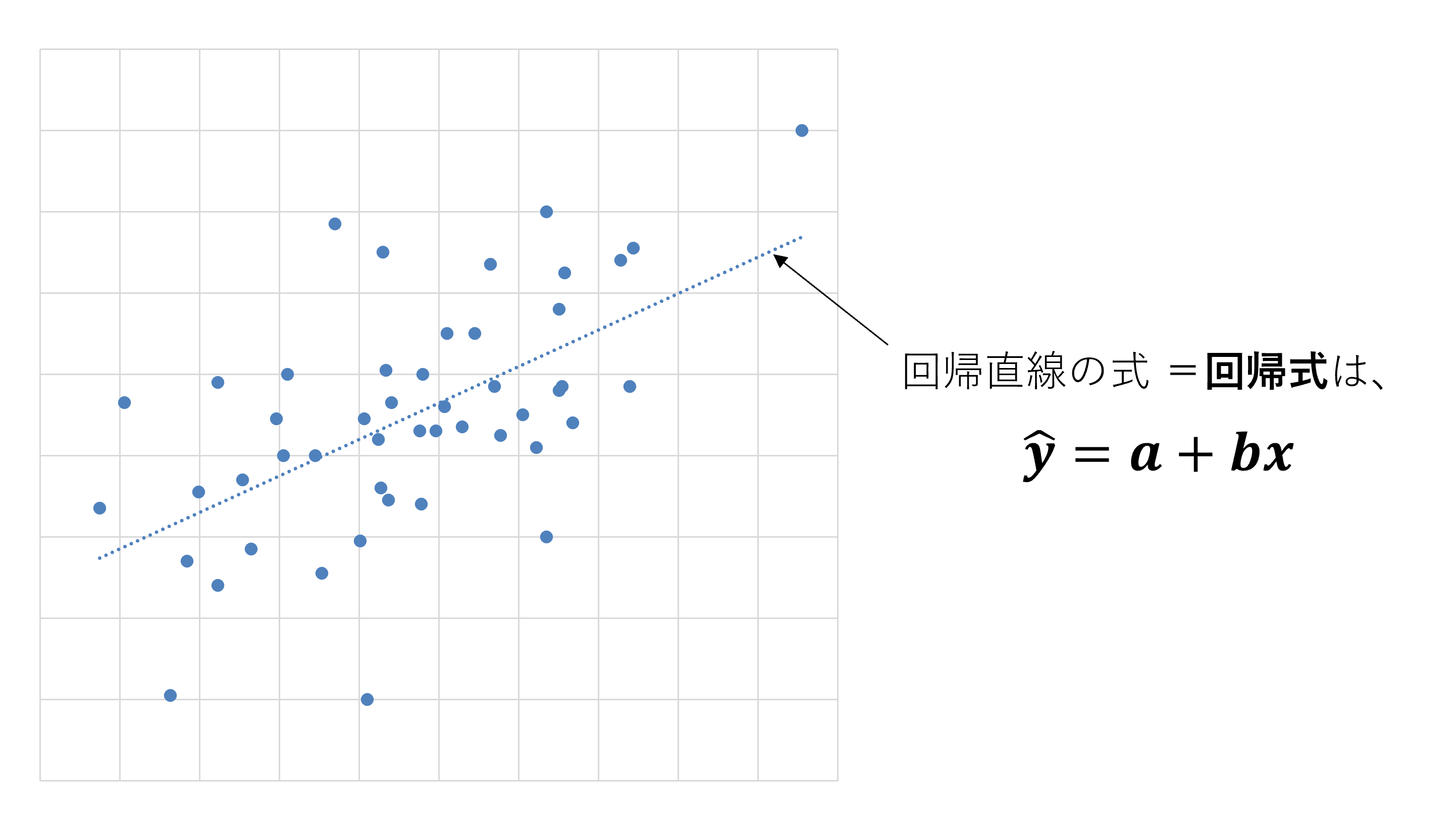
上図は、xとyのデータについて散布図を描き、回帰直線を引いたものです。回帰直線は直線の式になり、中学で学んだ一次関数と同様の式で表すことができます [2]。

回帰直線を一次関数の形で表した式を「回帰式」と呼びます。関心のある物事に影響するxのデータを取得すれば、それを回帰式のxに代入することで、それに対応したyの値を算出することができます。

ただし、回帰式が特殊なのは、通常の一次関数と異なり、y ̂（ワイハット）という記号が入っている点です。ハットは「予測された値（予測値）」を意味する記号です。

予測値と実測値の違い

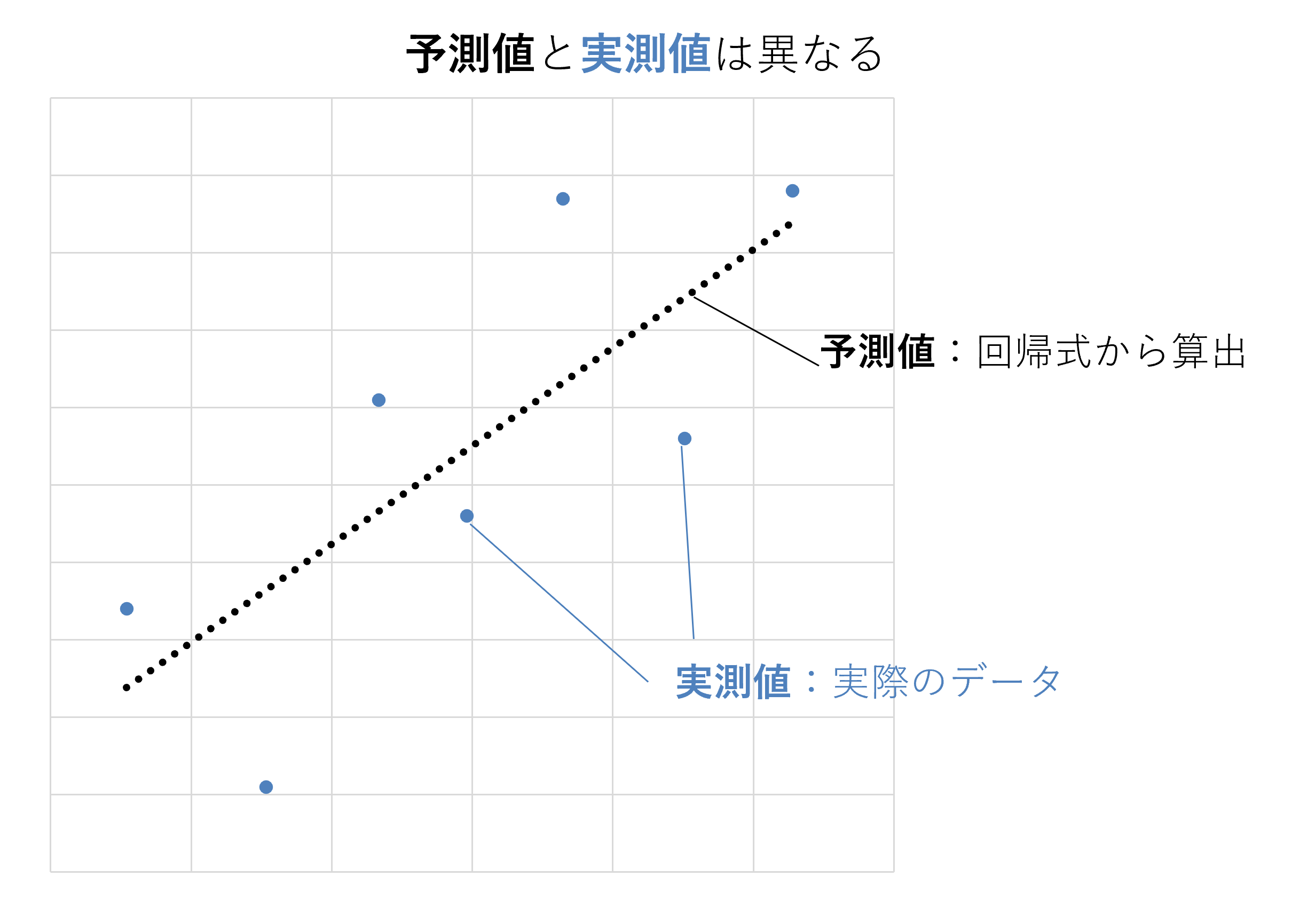
下図の通り、回帰直線と、実際に測定されたデータ（実測値）である各プロットとの間には、残差が存在します。そのため、xの値を代入して回帰式から計算されたyの値は、個々の実測値と常に一致するわけではありません。

回帰式によって得られるyの値は、あくまでxの値から予測されるyの値です。その特徴を強調するため、回帰式におけるyには、「予測された値」を表すハットがつけられています。

なお、ここでいう「予測」という表現は、「xのデータから”想定される”yの値を計算する」意味での予測です。「未来のことを予測する」という意味合いではありません。勘違いされることも多いため、注意しましょう。

xのデータの中心化

少し専門的な話になりますが、回帰式に含まれるxのデータは、事前に「中心化」の処理をします。中心化とは、取得したそれぞれのxのデータを、xの平均で引き算した値にすることを指します。例えば、取得したデータのxの平均が2.3点としたら、すべてのxの値から2.3を引いた値を作成するのが中心化です。

詳細な説明は割愛しますが、回帰分析では、中心化したデータをxの値として用いると、結果の解釈が容易になります。そのため、xのデータを中心化するとよいでしょう。

 

回帰式における切片の意味

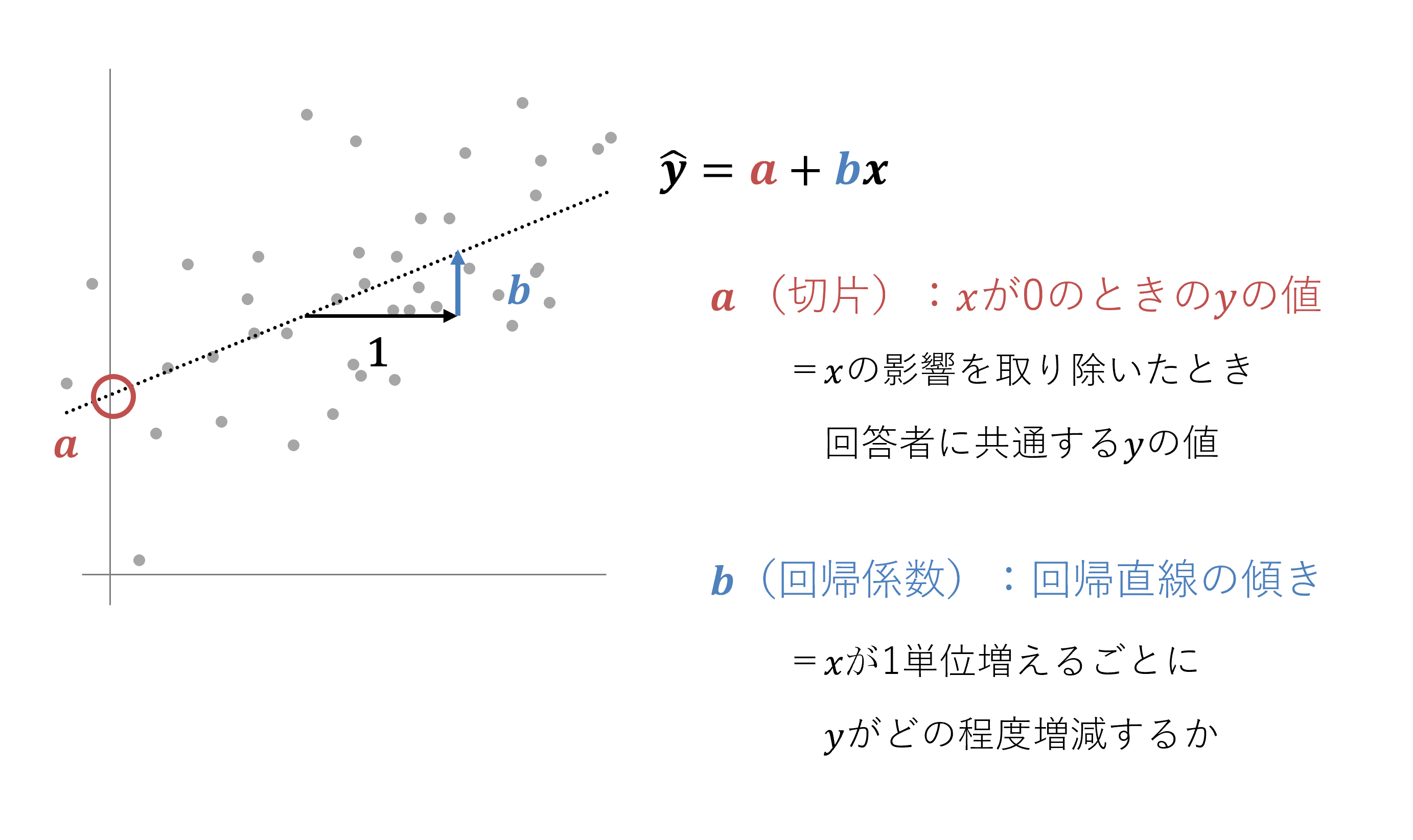
ここからは、回帰式の右辺に含まれる文字式について説明します。下図を見てください。

まず、回帰式のaは「切片」と呼ばれます。切片は、xの値が0のときのyの値です。なお、先ほど説明した中心化の処理により、xの値が0であることは、xの値が取得したデータの平均値であることを意味しています。切片の意味するところを言葉で表すと、「xの程度が平均的な状態を想定することでxの影響を取り除いた、すべての回答者に共通するyの程度」となります。

例えば、上司からの支援をx、エンゲージメントをyとします。それらのデータから求められた回帰式の切片aは、「上司からの支援が平均的な量あることを想定した上で、上司からの支援の影響を取り除いた、すべての回答者に共通するエンゲージメントの値」を意味します。個々の回答者が受けている上司からの支援の大きさに関係なく、すべての回答者が共通して持っているエンゲージメントの高さです。

 

回帰式における回帰係数の意味

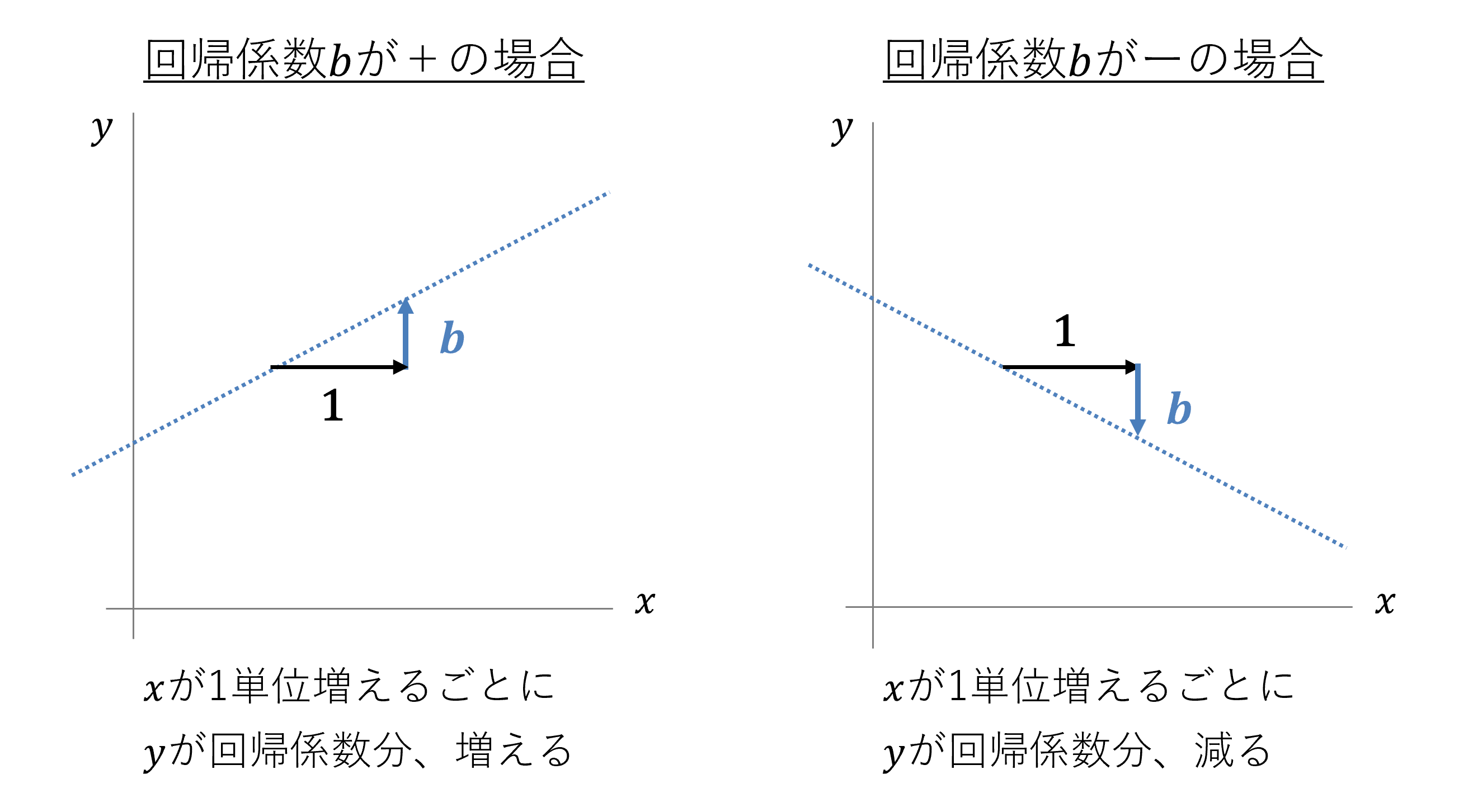
次に、回帰式のbは「回帰係数」と呼ばれます。回帰係数は、直線式の傾き、「xの値が増減したときに生じるyの変化の程度」を表します。もっとシンプルに言えば「xの、yに対する影響力」とも言えます。

回帰係数がプラスの値なら回帰直線は右肩上がりで、xの値が1ポイント増えると、yの値はbだけ増加します。回帰係数がマイナスの値なら回帰直線は右肩下がりで、xが1ポイント増えるとyはbだけ低下します。

 

 

yの実測値を用いた回帰式の表現

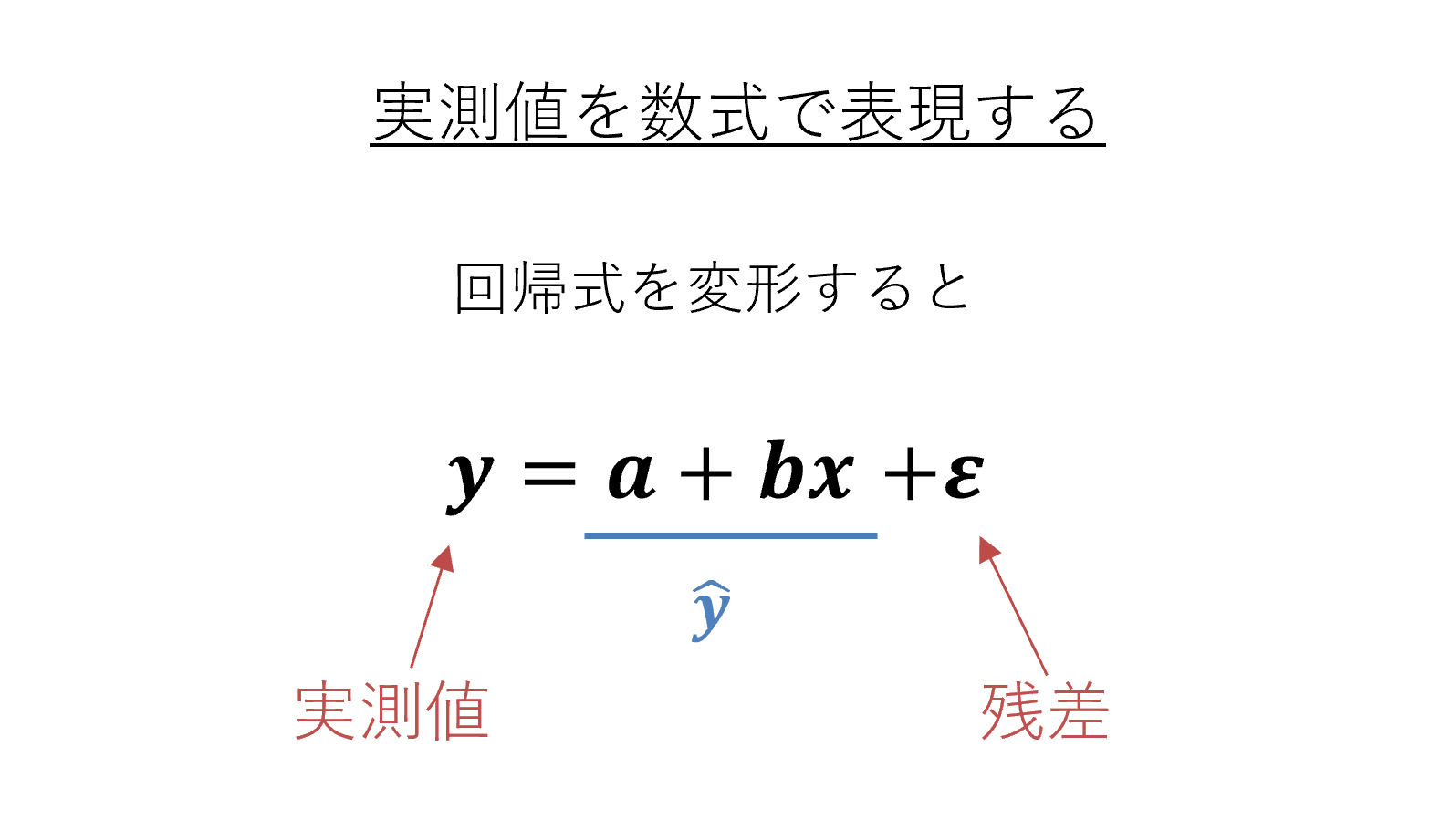
ここまで、回帰式で求められるyの値は実測値ではなく予測値（y ̂）である、という前提で話を進めてきました。しかし、yの実測値を用いて回帰式を表現することもできます。

先述の通り、予測値と実測値の間にはズレ＝残差が存在します。そのため、下図のように、回帰式で得られた予測値に残差を加えれば、実測値を表すことができます。yの値が予測値でなく実測値の式になったため、yからハットが外れています。

３．関心がある物事への説明力

要因では説明しきれない部分としての残差

「残差」について、もう少し説明します。回帰式における残差は「予測値と実測値のずれ」、さらに言えば「関心のある物事について、影響要因（関心のある物事に影響を与える要因）では説明しきれない部分」と解釈することができます。

yがエンゲージメント、xが上司からの支援とした場合、残差は「エンゲージメントについて、上司からの支援では説明しきれない部分」を意味します。冷静に考えればすぐに分かりますが、ある人のエンゲージメントは、何も上司からの支援の程度だけで決まりません。

例えば、職務内容が自分のスキルとフィットしていること、同僚と強いチームワークが発揮していることなど、他の要因も多数、エンゲージメントの高低には関係してくるでしょう。こうした諸々の要因の存在が残差を生み出しています。

 

要因で説明できている部分としての決定係数

残差は「関心のある物事について、影響要因では説明しきれない部分」を表しています。そのため、関心のある物事全体（100%）から、説明しきれない部分を引き算すれば、「関心のある物事について、影響要因が説明できている部分」を計算できます。これを、統計学的には「決定係数」（R2）と呼びます [3]。

決定係数は、「影響要因が関心のある物事をどの程度説明しているか（説明力）」を表す指標です。例えば、上司からの支援がエンゲージメントを促すことを想定した回帰式において、決定係数がR2 = .12と算出されたとします。それは、「上司からの支援によって、エンゲージメントの変動のうち12％が説明されている」ことを表します。

ここで気になることが出てきます。決定係数はどの程度の大きさなら良いのでしょうか。残念ながら、決定係数の大きさに絶対的な基準はありません。とはいえ、データ分析の慣習として、少なくとも.02以上、可能ならば.13以上あれば、「影響要因によって関心のある物事をある程度説明できている」と判断できます [4]。

 

 

４．複数の影響要因を取り上げた回帰分析(重回帰分析)

ここまでのところでは、影響要因（x）を1つだけ取り上げた回帰分析について解説してきました。ここからは、「複数」の影響要因を取り上げた回帰分析について見ていきましょう。

 

単回帰分析と重回帰分析の違い

初めに、ここまで用いてきた回帰式に含まれる用語について、統計学の用語に置き換えます。「関心のある物事（y）」は「従属変数」、「関心のある物事に影響する要因（x）」は「独立変数」と呼びます。

上司からの支援がエンゲージメントに影響することを検証した回帰式を思い出してください。そこにおいては、上司からの支援が独立変数、エンゲージメントが従属変数になります。このように独立変数が一つの回帰分析は「単回帰分析」と言います。

そして、独立変数が複数ある回帰分析は「重回帰分析」と呼ばれます。すなわち、これまで説明してきたのは単回帰分析、これから説明するのは重回帰分析になります。

 

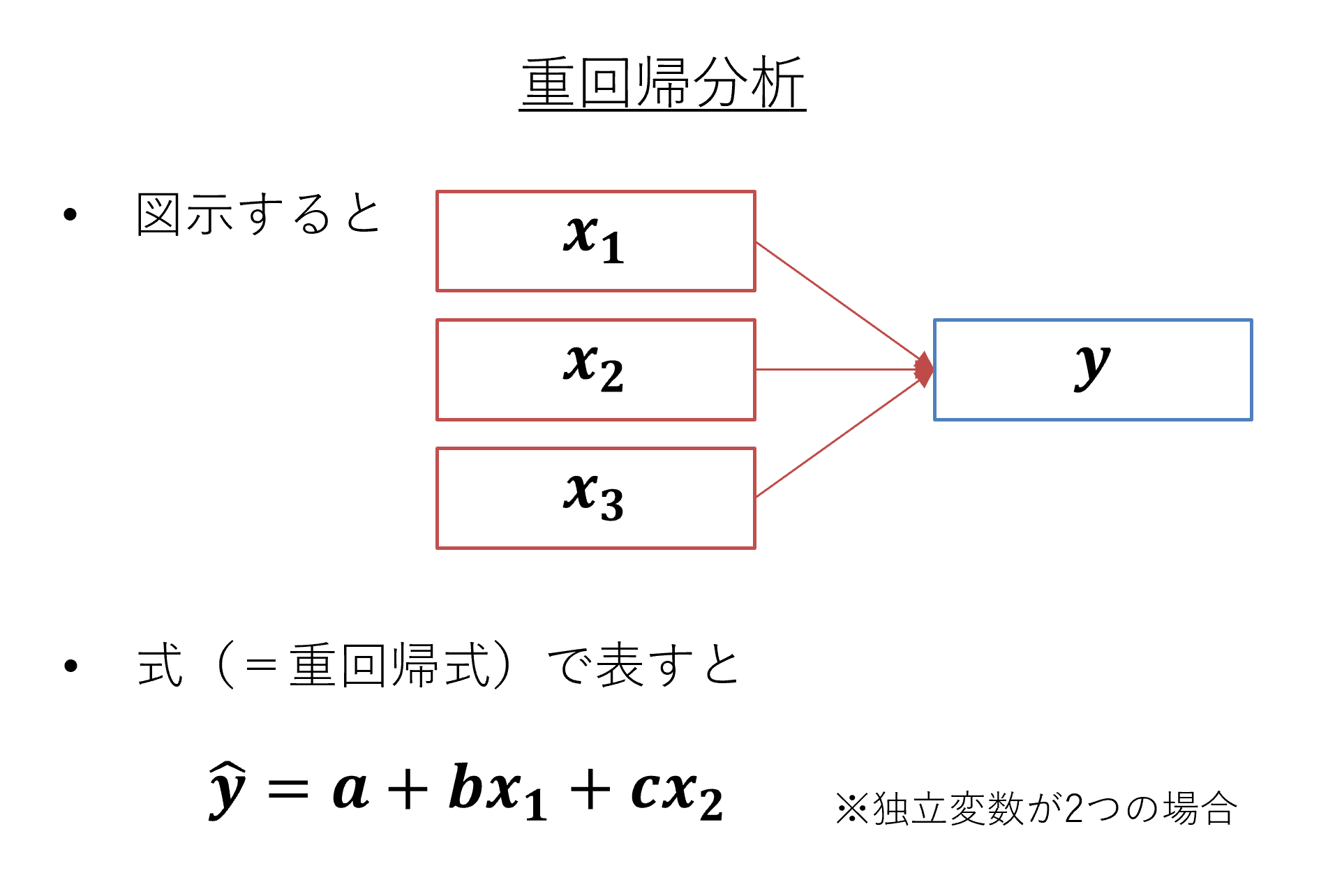
重回帰分析の回帰式

下図では、独立変数が2つの場合の重回帰分析の回帰式を示しています。独立変数が2つになったため回帰式のxも2つ(x1, x2)になっています。それぞれの独立変数に対応した回帰係数(b, c)もあります。重回帰分析においても、回帰係数や残差を計算し、決定係数（説明力）を算出することができます。

なお、重回帰分析における決定係数の計算に用いる残差は、「従属変数について、複数の独立変数によって説明しきれない部分」を指します。したがって、決定係数は「従属変数について、複数の独立変数によって説明できている割合」を表します。

 

それぞれの独立変数の影響力の比較

重回帰分析の強みが特に発揮されるのは、関心のある物事に対して、影響力のある要因を見定めたいときです。

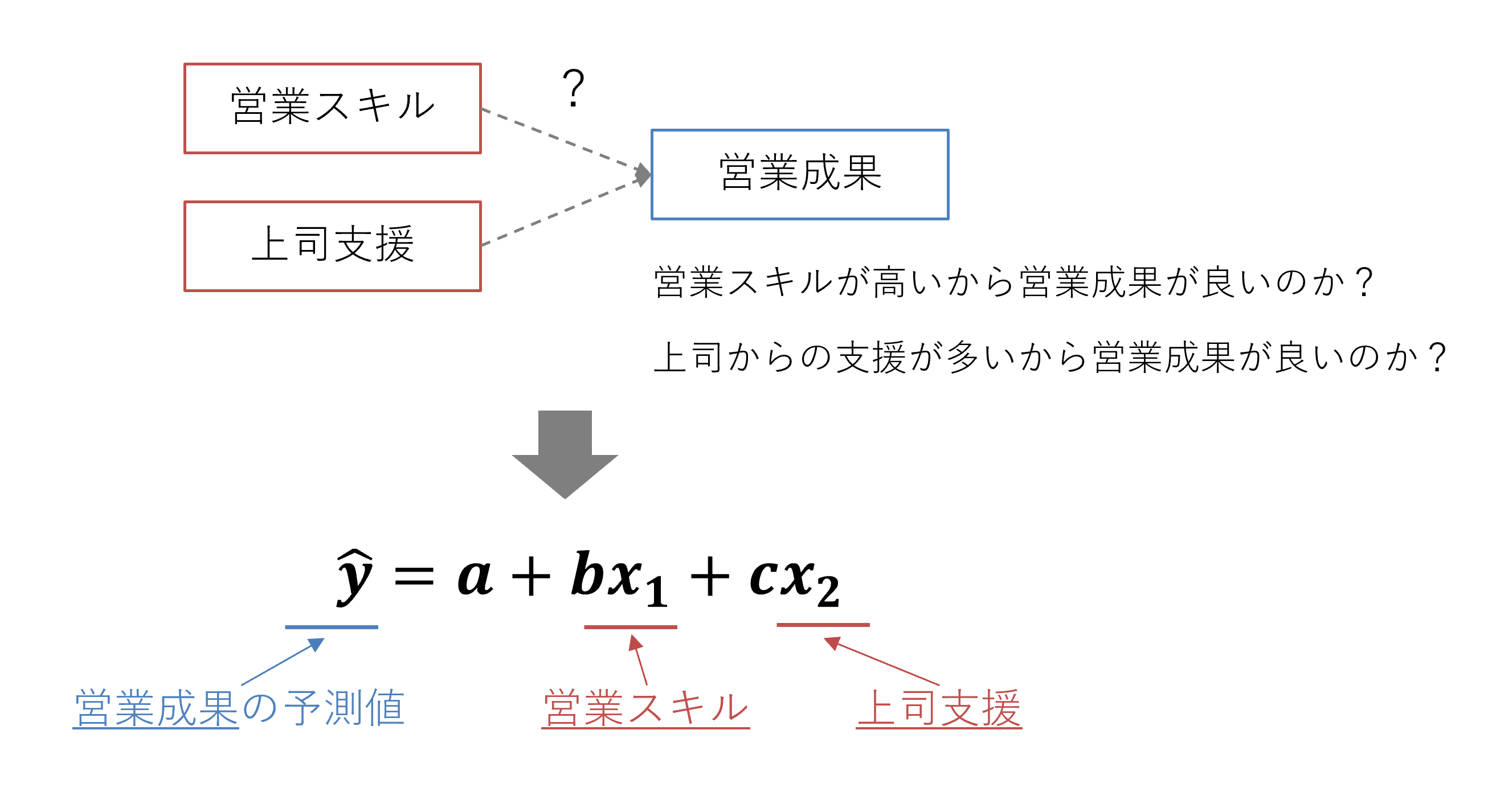
営業成果を従属変数（関心のある物事）とし、営業担当者の営業スキルの高さと、担当者の上司からの支援が独立変数（影響要因）だとします。重回帰分析によって、「各独立変数がそもそも従属変数に影響しているのか」「独立変数のうちどちらが特に有効に機能するのか」という疑問に答えることができます。

ここで特に注目に値するのは後者の疑問です。「営業スキルが高いから営業成果が良いのか、それとも、上司からの支援が多いから営業成果が良いのか」というような、影響力の相対比較をするということです。

 

偏回帰係数は単位に注意

重回帰分析の式における回帰係数には興味深い特徴があります。「ある独立変数x1において算出された回帰係数は、独立変数x2が従属変数yに及ぼす影響を取り除いた、純粋なx1の影響力を表す数値になっている」ということです。重回帰分析において、そのような性質を持った回帰係数のことを、特に「偏回帰係数」と呼びます[5]。

ただし、重回帰分析において偏回帰係数を確認する際に注意すべき点があります。得られたデータをそのまま用いた重回帰分析では、偏回帰係数の大きさを比較することはできません。偏回帰係数はそれぞれの独立変数に応じて算出されますが、独立変数によってデータの単位が異なるからです。

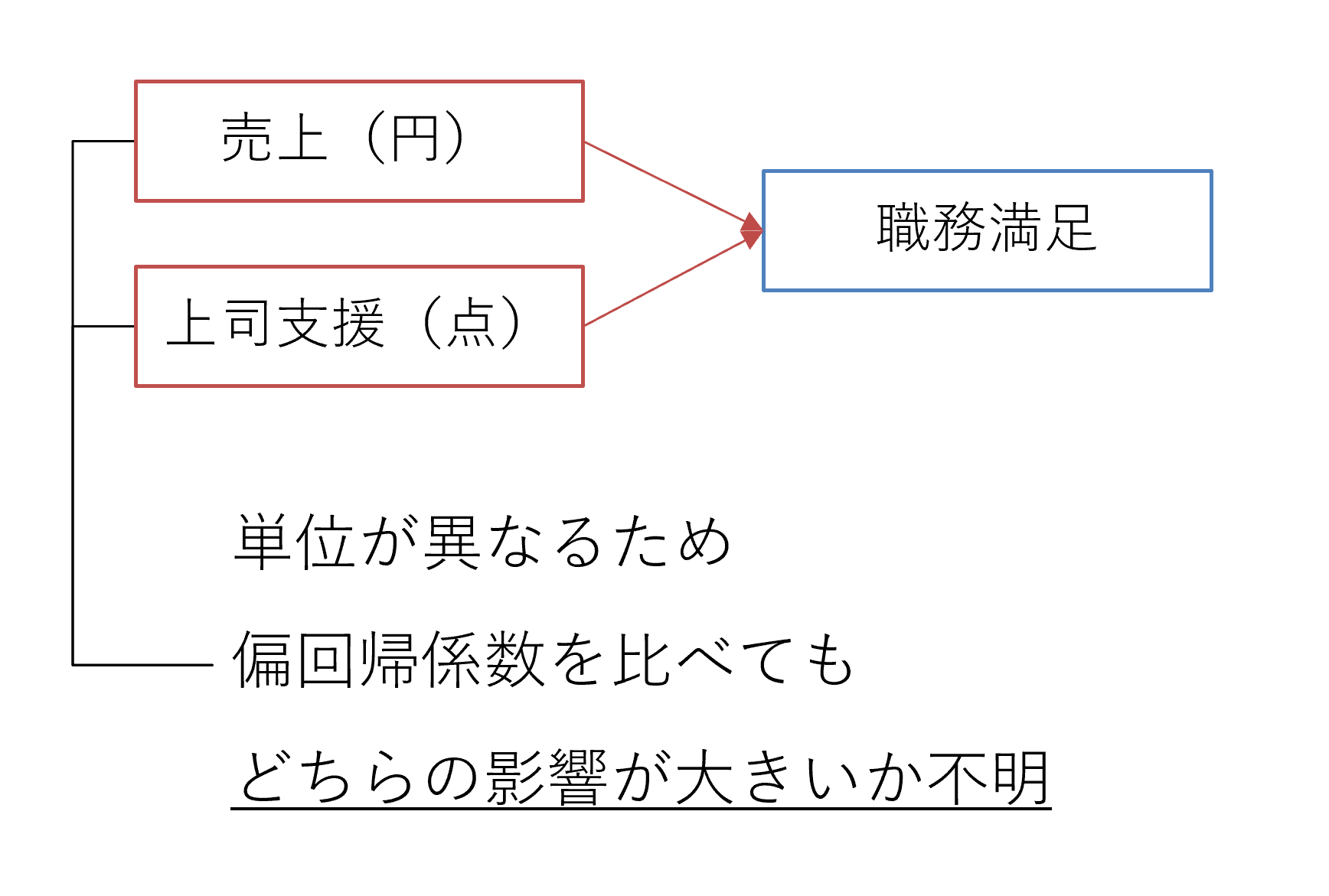
例えば、職務満足を高めるのは売上でしょうか、それとも上司からの支援でしょうか。そのことを確認するために、下図のように、職務満足を従属変数、売上と上司からの支援を独立変数にした重回帰分析を行いました。

重回帰分析の結果、売上と上司支援のそれぞれについて偏回帰係数が算出されます。しかし、売上は○円、上司支援では○点、とデータの単位が異なります。「10円の売上と10点の上司支援、どちらが職務満足により強く影響するか」といった比較になり、これでは偏回帰係数の大きさを解釈できません。

 

単位を揃えて比較する＝標準化

逆に言うと、データが持つ「単位」を揃えることができれば、重回帰分析における偏回帰係数の大きさを比較できます。統計学では、データが持つ単位の影響を除去するデータ変換法として「標準化」と呼ばれるものがあります [6]。

独立変数のデータを標準化した上で重回帰分析を行えば、偏回帰係数の大きさを比較できます。どの独立変数の影響力が相対的に大きいのかを検証できるのです。標準化したデータを用いて重回帰分析を行い、算出された偏回帰係数は、特に「標準化偏回帰係数」と呼ばれています。

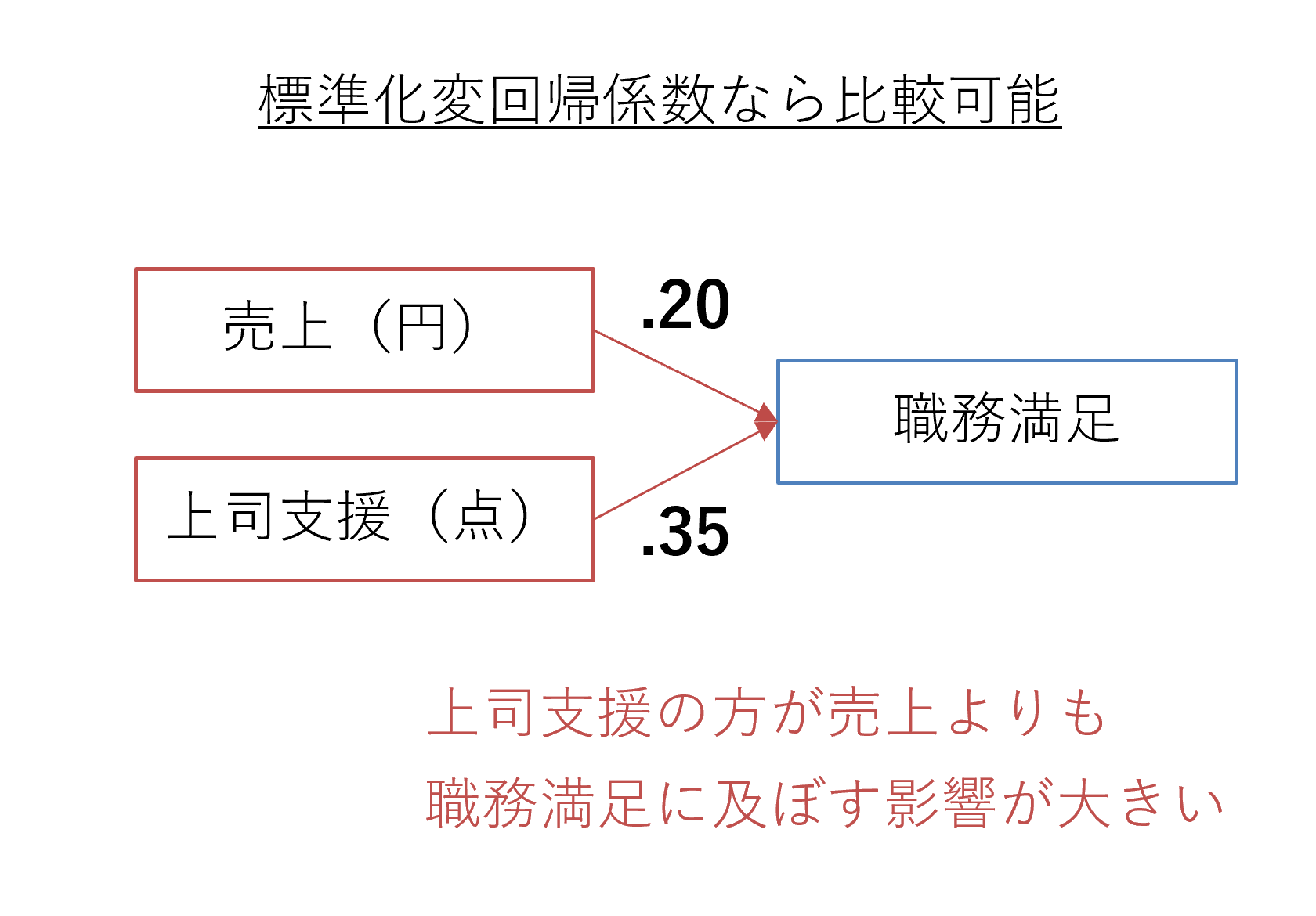
先の例を引き継ぎましょう。職務満足を従属変数、売上と上司支援を独立変数とした重回帰分析を行った例です。独立変数を標準化し、標準化偏回帰係数を求めたところ、売上が.20、上司支援が.35になりました。標準化偏回帰係数は、その大きさで影響力の比較ができます。そのため、「上司支援の方が売上よりも職務満足に及ぼす影響力が大きい」と解釈することができます[7] 。

この解釈を延長し、「職務満足を高めるには売上向上を図るよりも、上司から部下の支援を強化する方が有効」といった判断につなげられます。独立変数の影響力を比較すれば、重要な要因を特定できるため、対策の優先順位をつけることも可能です。

 

５．重回帰分析における「統計的に有意」の判断

ここまでお伝えしてきたのは、あくまでサーベイで得られたデータの中で、独立変数が従属変数にどの程度影響するかを検討する分析方法でした。

 

統計的に有意か否かの検討

しかし実際には、サーベイに回答した従業員だけの状態を知りたいのではなく、回答しなかった従業員にも当てはまるような一般的な傾向かを知りたいことも多いと思います。

統計学では、データ分析の結果を一般化できるか否かを判断するために、分析結果が“統計的に有意か否か”を検討します。“統計的に有意”については別のコラム[8] にて詳細に解説しているため、そちらを参考にしていただきたいのですが、端的に言えば、「一部の回答者（標本）における分析結果が、サーベイで明らかにしたい対象者全体（母集団）にあてはまると統計学的に判断できる状態」を指します。

統計的に有意か否かを検討すれば、組織サーベイのデータで見出された分析結果が、そのデータだからこそ偶然出たものなのか、それとも、組織メンバー全体にあてはまるものなのかを判断することができます。

 

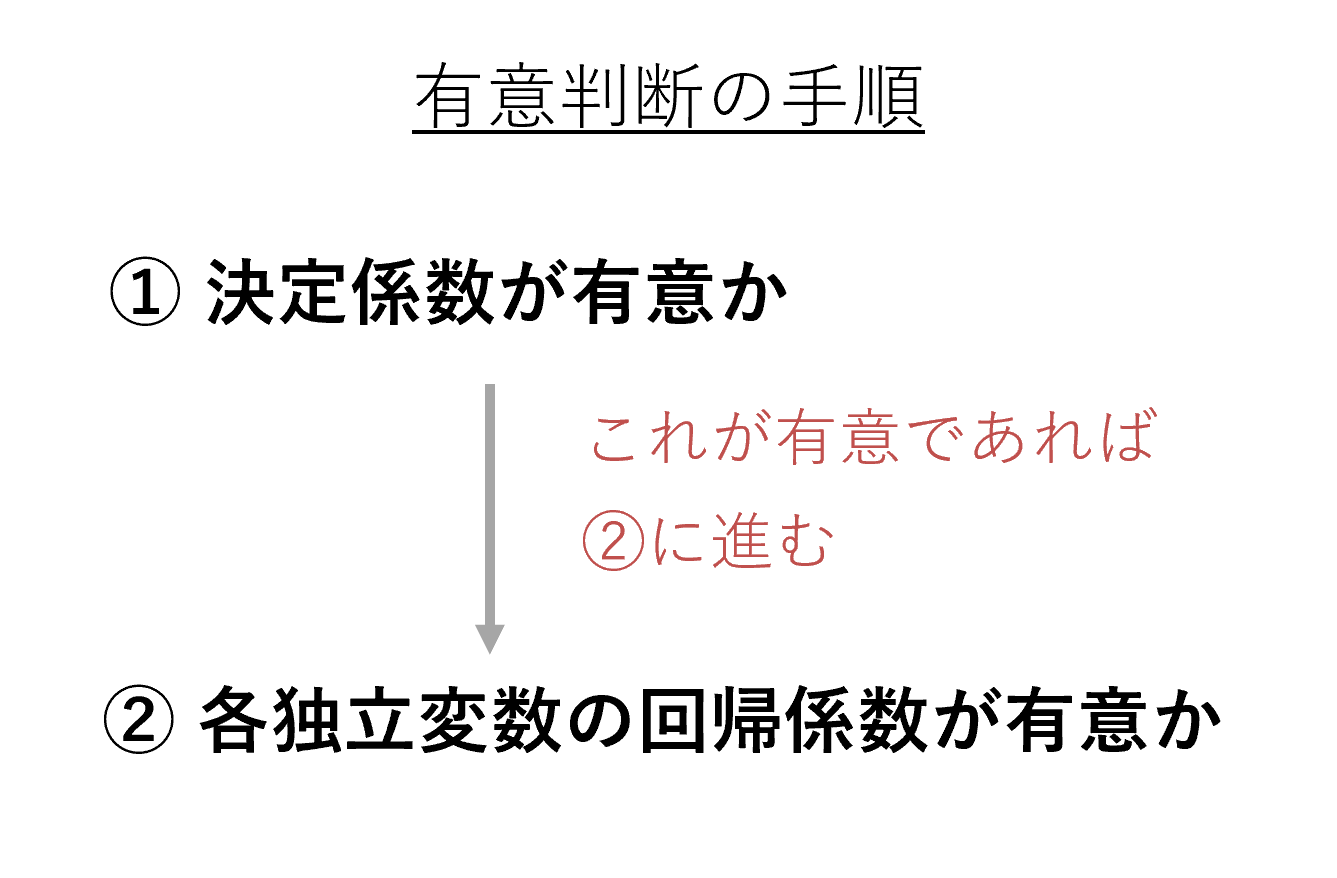
決定係数が統計的に有意か

重回帰分析では、統計的に有意か否かの判断を2段階に分けて行います。最初に、重回帰分析によって算出された「決定係数」が統計的に有意か否かを判断します。少々専門的な表現になってしまうのですが、具体的には、「算出された決定係数の値から、“母集団の決定係数が0でない”といえるか」を検討します。

重回帰分析で算出される決定係数は、既述の通り、「従属変数について、複数の独立変数によって説明される部分」を意味します。仮に、母集団における決定係数の値が0であると判断されたら、どうなるでしょう。それは、「母集団においては、今回の分析で取り上げた複数の独立変数では、従属変数を全く説明できない」ということになります。

例えば、重回帰分析の結果、「職務満足に対して売上より上司支援の方が影響力は大きい」ということが分かったとしても、それは、あくまでその分析に用いたデータでのみ当てはまる傾向であり、一般化は難しい、となるのです。そうなってしまうと、せっかくの分析結果も活用しにくくなります。

そこで、重回帰分析では初めに、決定係数が有意か否かを判断します。仮に決定係数が統計的に有意だと判断されたら、「母集団において、分析で取り上げた複数の独立変数によって、従属変数を説明することができている」とわかります。分析結果が一般化できそうだという解釈が可能になるのです。

 

回帰係数が統計的に有意か

重回帰分析における決定係数について統計的に有意であることが確認できたら、次は、各独立変数の回帰係数が有意か否かを判断します。これも専門的な表現になりますが、具体的には「母集団において、“各独立変数の回帰係数の値は0でない”といえるか」を検討します。

ここでも、「母集団において、ある独立変数の回帰係数は0である」と判断された場合を考えてみましょう。それは「その独立変数が従属変数に及ぼす影響は、母集団では実質的にはない」ことを表します。例えば、重回帰分析の結果、売上が職務満足に影響することが分かったとしても、その結果が統計的に有意ではないなら、今回集めたデータを超えた範囲まで分析結果を一般化できないということです。

逆に、回帰係数が統計的に有意だと判断されれば、「独立変数が従属変数に及ぼす影響は、母集団でも認められる」とわかり、その独立変数に影響力があることが示されます。

この手続きにより、母集団において影響力が実質的にないと判断された独立変数と、影響力が認められた独立変数が区別されます。どの要因が関心のある物事に影響しているか、組織メンバー全体に一般化して判断することができます。

６．重回帰分析の注意点

多重共線性に注意

最後に、重回帰分析を実施するにあたって注意すべきポイントを2点挙げます。一つは、重回帰分析の分析結果の確実性を損ねる要因についてです。

重回帰分析の計算のプロセスでは、独立変数のデータ間に強い関連（相関）があると、回帰係数の値の計算がうまくできなくなります。このような問題は「多重共線性」あるいは、その英単語であるmulticollinearityを略して「マルチコ」と呼ばれています。

多重共線性を避ける最も良い手段は、強い関連がありそうな独立変数を同時に用いないようにすることです。

例を挙げましょう。従業員のエンゲージメントを高める要因を検討したいとします。独立変数としては、「職場の人間関係の良さ」と「職場のチームワークの良さ」を取り上げました。しかし、これらの独立変数には、強い関連があると考えられます。人間関係が良いほどチームワークも良いことが、あるいは、人間関係が悪いほどチームワークも悪いことが容易に想像できるからです。

これらの独立変数をそのまま重回帰分析に含めて分析をすると、多重共線性が発生します。その結果、算出された偏回帰係数の値が正確でない可能性が大きくなります。そこで、「職場の人間関係の良さ」と「職場のチームワークの良さ」のいずれか一方を取り除いて重回帰分析を行います。

多重共線性はなかなか厄介な問題です。得られた偏回帰係数の値が正確でないと、それに基づいた解釈や意思決定も誤ってしまうからです。重回帰分析をする際には、独立変数に似通ったものを取り上げないようにしましょう。

 

重回帰分析は因果関係をただちに保証しない

もう一つの注意点ですが、重回帰分析は、その分析によって「因果関係」が保証されるわけではないという点です。

重回帰分析では回帰式や決定係数、標準化偏回帰係数などを求め、それらによって独立変数が従属変数に及ぼす影響を解釈します。しかし、重回帰分析の分析結果「だけ」で因果関係が保証されることはありません。

サーベイの分析結果から因果関係を主張するには、そのサーベイの背景にある現場での実践知や学術的な知見から、因果関係が想定されることをしっかり説明するなど、統計分析の範疇を超えた手続きが必要になります。

あるいは、因果関係を強く保証できるような組織サーベイを設計することも一策です。そのような組織サーベイの一つとして、時系列でのデータ収集を含む設計が考えられます。

回帰分析は、データ分析に基づく意思決定を行う上で有用な方法です。回帰分析の考え方や各データが意味するところを理解し、実践に活かしていただければと思います。

(了)

---

[1] 最小二乗法は、厳密には各残差を二乗した値の合計を算出しています。そのため、最小”二乗”法と呼ばれます。残差を二乗して扱うのは、プロットが回帰直線の上部にあるときはプラスの残差、プロットが回帰直線の上部にあるときはマイナスの残差となり、それらをそのまま合計すると、残差が正負で打ち消し合ってしまうからです。この問題を回避するために、残差を二乗します。

[2] 回帰分析は、データが数量としての意味を持っている、いわゆる「量的データ」を用いて分析するのがベターです。例えば、売上額や労働時間、数値で回答した上司支援の程度などのデータは量的データに該当します。他方、部署の違いや曜日などのデータは、データ上では”月曜＝1, 火曜＝2…”など数値化することはできますが、その数値には数量的な意味はなく、識別ラベルとしての数値割り振りです。このようなデータは質的データと呼ばれ、回帰分析にそれを含める際には、特殊な分析手続きが必要になります。

[3] 残差から決定係数の値を算出する方法のほかに、回帰式で得られた予測値と実測値の相関係数を算出し、その相関係数を二乗することで、決定係数を算出する方法もあります。

[4] 次の文献を参考にしています。Cohen. J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). Hillsdale, NJ: Lawrence Erlbaum.

[5] 少し複雑なので、先の例を用いて改めて説明してみましょう。偏回帰係数(b)の値は、営業スキル(x1)が営業成果に及ぼす影響力を表します。それは、上司支援(x2)が平均的な程度であることを想定した上で、上司支援が営業成果に及ぼす影響(c)を取り除いて算出されたものになっています。すなわち、偏回帰係数(b)は、上司支援の高さとは関係しない、営業スキルが独自に営業成果に及ぼす影響力を意味するわけです。

このような偏回帰係数の特徴を、上司支援の偏回帰係数(c)も持っています。そのため、上司支援の偏回帰係数も、営業スキルによる影響を除いた、上司支援が独自に営業成果に持つ影響力を表します。

[6] 標準化においては、取得したそれぞれのx（独立変数）のデータすべてを、xの平均で引き算し、さらにそれをxの標準偏差（データの散らばりを示す指標の一つ）で割り算した値にします。取得したデータのxの平均が2.3点、標準偏差が0.6点としたら、それぞれのデータのxの値から2.3を引き、その値を0.6で割り算した値を作成します。これが、単位の影響を除去する標準化です。

[7] なお、「上司支援があることで売り上げが高まり、それによって職務満足も高まる」というように、分析で取り上げた影響要因の間にも影響プロセスがあることが強く想定される場合、算出された標準化偏回帰係数の値はやや不正確なものになります。そのような場合は、構造方程式モデリングなど影響プロセスの検証に特化した他の分析法を用いる必要があります。

[8] 統計的に有意に関する詳しい解説は、弊社サイトに掲載してあります。

セミナーレポート：人事のためのデータ分析入門「統計的に有意」とは何か

セミナーレポート：「統計的に有意」とは何か？

---

執筆・監修

伊達 洋駆
神戸大学大学院経営学研究科　博士前期課程修了。修士（経営学）。2009年にLLPビジネスリサーチラボ、2011年に株式会社ビジネスリサーチラボを創業。以降、組織・人事領域を中心に、民間企業を対象にした調査・コンサルティング事業を展開。研究知と実践知の両方を活用した「アカデミックリサーチ」をコンセプトに、組織サーベイや人事データ分析のサービスを提供している。近著に『オンライン採用 新時代と自社にフィットした人材の求め方』（日本能率協会マネジメントセンター）や『人材マネジメント用語図鑑』（共著；ソシム）など。

 

 

能渡 真澄
信州大学人文学部卒業，信州大学大学院人文科学研究科修士課程修了。修士（文学）。現在は，筑波大学大学院人間総合科学研究科に在籍。価値観の多様化が進む現代における個人のアイデンティティや自己意識の在り方を，他者との相互作用や対人関係の変容から明らかにする理論研究や実証研究を行っている。高いデータ解析技術を有しており，通常では捉えることが困難な，様々なデータの背後にある特徴や関係性を分析・可視化し，その実態を把握する支援を行っている。