2025年7月4日
区間推定:幅を持たせて不確実性を考慮する
私たちの身の回りには、様々な数字があふれています。企業の人事部門においても、従業員のエンゲージメントスコアや離職率など、多くの指標を扱います。しかし、これらの数字は本当に正確なのでしょうか。
例えば、皆さんの会社で組織サーベイを実施し、100点満点中の平均点が68点だったとします。この68点という数字は、本当に全従業員の真の満足度を表しているのでしょうか。
実は、この68点という数字には、ある種の曖昧さが含まれています。私たちが得られるのは、ある時点での一部の従業員の回答に過ぎないからです。全従業員の真の満足度は、もしかしたら66点かもしれませんし、70点かもしれません。
こうした曖昧さを考慮に入れながら、データから得られる情報を活用する方法が「区間推定」です。区間推定を理解することによって、数字の持つ意味を深く理解し、より賢明な意思決定ができるようになります。
本コラムでは、区間推定の考え方を解説します。前半は概念的な説明を、後半は少し技術的に説明を掘り下げます。
点から幅へ
点推定
私たちが日常的に目にする統計情報の多くは、「点推定」と呼ばれるものです。点推定とは、ある集団全体の特性を、単一の数値で表現しようとする方法です。
例えば、組織サーベイで満足度の平均点が68点だったという結果は点推定の一例です。この方法では、データの全体的な傾向を一つの代表的な値で示すことで、簡潔に情報を伝えることができます[1]。
しかし、点推定には限界があります。それは、データのばらつきや不確実性を考慮していないことです。実際のデータには常にある程度のばらつきがあり、またサンプリングなどに伴う誤差も存在します。68点という数字だけを見ていては、このような側面を捉えることができません。
区間推定
そこで「区間推定」の出番となります。区間推定は、点推定の限界を克服する方法で、推定値を単一の数値ではなく、ある範囲(すなわち、区間)で表現します。区間推定においては、データの不確実性を示すことができ、より現実的な解釈が可能になります。
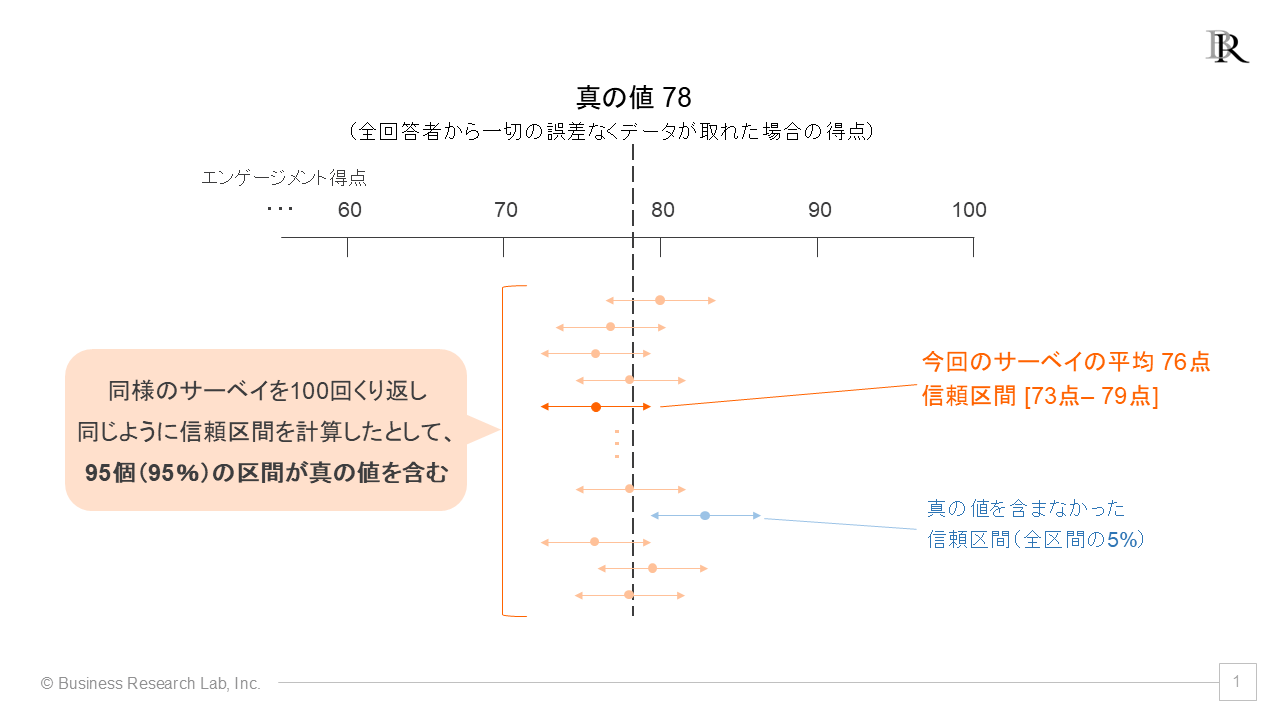
例えば、「従業員の満足度は平均が76点であり、真の値は73から79点の間にあると考えられる」といった形で、範囲を伴うよう結果を表現します。この「73点から79点」という範囲を「信頼区間」と呼びます。信頼区間は、真の値が含まれるであろう範囲のことを表しています。真の値とは、「全従業員から誤差なく測定できた、真のエンゲージメント平均」といった、一部のデータであるサーベイでは捉えられない本来の全体的な特徴・傾向を表す値のことです。
この信頼区間を計算する際には、95%など「信頼水準」と呼ばれる値を決めます。信頼水準は、同様のサーベイを繰り返し行い、点推定に同じ推定方法を用いた場合に、繰り返し行ったサーベイで算出した信頼区間のうち、真の値が含まれるものの割合を示しています。
文章による説明だとややわかりにくいので、下の図で信頼水準と信頼区間の意味を見てみましょう。
サーベイで全従業員の回答を集めることは難しく、一部の従業員から回答が集まることになります。あるいは、サーベイを実施した日に、ある従業員が仕事で大きな成功を収めて気分が良い状態で回答し、普段よりもポジティブな回答をしてしまうかもしれません。そのような様々な要因を含み、サーベイごとに算出される平均は少しずつ違ってくると考えることができます。
そのため、各サーベイで算出される信頼区間も様々になりますが、それに対して真の値はひとつしかありません。すると、各サーベイの信頼区間のうち、真の値を含む区間と含まない区間が現れてきます。これらの区間推定に関して、「全体の95%が真の値を含む」ように区間を計算したとき、95%が信頼水準となります。また、この信頼水準で推定された信頼区間を「95%信頼区間」と呼びます。
区間推定の利点は二つあります。ひとつは、真の値がどの程度の値になるか、あたりをつけられることです。信頼水準が高い信頼区間は、その中に真の値を含んでいる可能性が高く、おそらく真の値はその中にあるだろうと見なして読み取ることが多いです[2]。これにより、区間による幅がありつつも、「今回のサーベイから、従業員の満足度はおよそ73~79点なのだろう」と、全体の傾向を判断できます。
加えて、信頼区間により点推定の不確実性を表現できるメリットもあります。例えば、信頼区間が66点から86点と広ければ、その解釈は「今回のサーベイではエンゲージメント平均が76点と示されたが、真の値は66点から86点の間にあると考えられる」となり、そのサーベイにおける真の値の推定精度が低いことがわかります。信頼区間の幅が広い場合は、結果を慎重に受け止める必要があります。
具体例
ある企業で、部署ごとのエンゲージメントスコアを比較しました。営業部門の平均スコアが3.8、製造部門の平均スコアが3.6だったとします(5点満点)。平均による点推定だけを見ると、営業部門の方が製造部門よりもエンゲージメントが高いと結論づけるかもしれません。その結果、製造部門のエンゲージメント向上に予算を割り当てることもあり得ます。
しかし、これらの数値には不確実性が含まれています。例えば、営業部門の95%信頼区間が[3.5, 4.1]、製造部門の95%信頼区間が[3.3, 3.9]だったとしましょう。二つの部署で信頼区間が重なっており、各部門全体の傾向では、もしかすると製造部門の方が営業部門よりエンゲージメントが高いかもしれません。この情報を考慮すると、両部門のエンゲージメントに統計的に有意な差があるとは言い切れなくなります。
区間推定を行わずに点推定だけで判断すると、実際には有意な差がないにもかかわらず、製造部門のエンゲージメント向上に過剰な資源を投入してしまうおそれがあります。また、営業部門と製造部門の差について、存在しない要因を探そうとして時間と労力を無駄にする可能性もあります。
製造部門の従業員に「エンゲージメントが低い」と伝えることによって、実際には問題がないにもかかわらず、モチベーションを下げてしまうことになったら問題です。点推定の結果だけを経営陣に報告すれば、会社の状況に対する誤った認識を与えかねません。
区間推定を行わないと、データの不確実性を無視した判断をしてしまい、結果として誤った意思決定や不適切な施策につながる可能性があります。区間推定を用いることで、このようなリスクを軽減し、より慎重な判断が可能になるというわけです。
区間推定の掘り下げ
ここからは、区間推定の背後にある統計学の基本的な考え方を掘り下げます。
母集団とサンプル
統計学においては、調査や分析の対象となる全体を「母集団」と呼びます。例えば、ある会社の組織サーベイを考えたとき、その会社の全従業員が母集団となるかもしれません。
母集団は、私たちが本当に知りたい対象全体を指します。しかし、実際には、この母集団全体を調査することは難しく、コストや時間など様々な制約から、その一部のみを調査することがほとんどです。
この調査対象となる一部を「サンプル」(標本)と呼びます。例えば、1000人の従業員がいる会社で、400人を調査した場合、この400人がサンプルとなります。
サンプルは母集団の一部であり、母集団の特性を推測するための手がかりとなります。そして、この「推測」のプロセスが統計分析のエッセンスです。限られた情報(サンプル)から、全体(母集団)の特性を推し量ることが目的といえます。
確率分布と正規分布
確率分布は、ある指標がとりうる値とその確率を表す概念です。これは、データの特性を理解する上で重要な役割を果たします。
確率分布を通じて、データの傾向やパターンを把握することができます。データがどのような値をとりやすいか、どの程度ばらつきがあるかなどの情報を、確率分布を通じて理解することができます。
多くの自然現象や社会現象では、データが正規分布と呼ばれる特殊な形の分布に従うことが知られています。正規分布は釣鐘型の対称な形をしており、中心(平均)付近の値が最も出現しやすく、両端に行くほど出現頻度が低くなります[3]。
正規分布は、多くの統計的手法の基礎となる概念です。特に、後述する中心極限定理との関連で、区間推定において重要な働きをします。
標準誤差と中心極限定理
サンプルから計算された平均値は、必ずしも母集団の真の平均と一致しません。これは、サンプリングの過程で様々な影響を受けるためです。例えば、組織サーベイで特に満足度の高い(または低い)従業員が多くサンプルに含まれてしまうと、サンプル平均は母集団平均よりも高く(または低く)なってしまいます。
このサンプル平均がサンプリングごとに母集団平均からどれだけばらつくのか、その「ずれ」の大きさを表すのが標準誤差です。標準誤差は、サンプリングによって生じる誤差の大きさを示します。もし同じ母集団から多数サンプリングを行い、それぞれのサンプルの平均を計算した場合、それらのサンプル平均がどの程度ばらつくかを表します。標準誤差が小さいほど、サンプル平均が母集団の平均に近いと考えられます。
標準誤差は、サンプルサイズが大きくなるほど小さくなります。これは直感的にも理解できるでしょう。10人に聞いた結果よりも、1000人に聞いた結果の方が、そのデータで算出される平均は真の値に近いはずです。標準誤差は標準偏差をサンプルサイズの平方根で割り算すると算出でき、サンプルサイズの平方根に反比例して小さくなります。サンプルサイズを4倍にすると、標準誤差は半分になります[4]。
ここで重要になるのが、中心極限定理という原理です。中心極限定理は、サンプルサイズが十分に大きければ、サンプル平均の分布が正規分布に近づくことを意味します[5]。同じ母集団から多数のサンプルを取り、それぞれのサンプル平均を計算すると、そのサンプル平均の分布は正規分布に従うというものです。
中心極限定理の大事な点は、元のデータの分布に関わらず、サンプル平均の分布が正規分布に近づくことです。たとえ個々の回答がばらついていても、その平均値は正規分布に従うという性質があります[6]。
中心極限定理、正規分布、区間推定の関係を整理しましょう。
中心極限定理によって、サンプル平均の分布が正規分布に従うことがわかります。この性質を利用することで、サンプル平均がどの程度、母集団平均の周りにばらつくかを正規分布に基づいて予測できます。
具体的には、正規分布の性質から、サンプル平均が真の平均の周りにどのように分布するかを数学的に記述することができます。例えば、サンプル平均は約68%の確率で真の平均の±1標準誤差の範囲内に、約95%の確率で±2標準誤差の範囲内に収まることがわかります[7]。
この予測を基に、母集団平均が含まれると考えられる区間を推定します。これが区間推定なのです。サンプルから得られた情報と正規分布の性質を組み合わせることで、母集団の平均がどの範囲にありそうかを推測するということです。先ほど図で示した通り、例えば95%信頼区間は、この推定方法を100回繰り返した場合、そのうち95回は真の値を含む区間を得られることを意味しています。
信頼区間の算出
以上を踏まえて、信頼区間を計算する方法を見ていきましょう。4つの段階に分けて説明します。
- サンプル平均(x)とサンプルの標準偏差(s)を計算します。サンプル平均は、全ての観測値の合計をサンプルサイズで割ったものです。標準偏差は、データのばらつきを表し、各観測値と平均との差の二乗の平均の平方根として計算されます。
- 目的の信頼水準(例えば、95%)に対応するzスコアを決定します[8]。zスコアは、標準正規分布上で特定の確率に対応する値です[9]。標準正規分布とは、平均が0、標準偏差が1の正規分布のことで、正規分布は標準正規分布に変換することができます。95%信頼区間の場合、z≈1.96です。これは、標準正規分布において、中心から左右1.96標準偏差の範囲内に95%のデータが含まれることを意味します。標準正規分布上で、中心から左右に1.96離れた点の間に95%の面積(確率)が含まれるということです。
- 「SE=s/√n」という式で、標準誤差(SE)を計算します(nはサンプルサイズです)。標準誤差は、サンプル平均のばらつきの程度を表す指標です。サンプルの標準偏差(s)をサンプルサイズ(n)の平方根で割ることで計算します。これは、中心極限定理に基づいています。中心極限定理によって、サンプル平均の分布の標準偏差(すなわち、標準誤差)は、母集団の標準偏差を√nで割ったものに近づくことがわかっています[10]。
- 「[x-z*SE, x+z*SE]」という形で、信頼区間を計算します。これは、サンプル平均(x)を中心に、zスコアと標準誤差の積だけ上下に広げた範囲を意味します。この計算方法の根拠は、中心極限定理と正規分布の性質にあります。中心極限定理により、サンプル平均の分布は正規分布に従います。正規分布の性質を利用すると、平均からある範囲内にデータが含まれる確率を計算できます。例えば、平均±1.96標準偏差の範囲に95%のデータが含まれます。サンプル平均の分布の標準偏差が標準誤差なので、サンプル平均±1.96×標準誤差の範囲に、真の平均が含まれるだろうと考えられます。これにより、信頼区間を計算できます。
解釈の注意点
こうして導き出した範囲内に、母集団の真の平均が含まれると考えられます。ただし、その解釈には注意しなければなりません。
95%信頼区間の場合、「もし同じ方法で多数(理論的には無限回)調査を行った場合、その多数の調査それぞれで構成した信頼区間のうち95%に真の平均が含まれる」という意味です。この解釈は少し複雑ですが、実務上は「母集団の真の平均が高い確率でこの範囲内にある」と理解しておけば十分でしょう。
ただし、100%の確実性はないことを常に意識しておくことが大事です。例えば、95%信頼区間であれば、20回のうち1回程度は真の値を含まない区間を得る可能性があります[11]。したがって、信頼区間を用いる際は、この不確実性を念頭に置きつつ、慎重に判断を行いましょう。
信頼区間の解釈には、他にも考慮すべき点があります。
初めに、信頼区間は母集団パラメータの範囲を示すものであり、個々のデータの範囲ではありません。全てのデータがこの範囲内に収まるわけではなく、「母集団の平均値が」この範囲内にあるだろうと推定されるということです。
例えば、組織サーベイで95%信頼区間が3.5から4.0だったとしても、個々の従業員のスコアはこの範囲外になることもあります。信頼区間は、あくまで母集団全体の平均に関する推定であり、個々のデータの分布を直接表すものではありません。
続いて、信頼区間が重なっていても、必ずしも統計的に有意な差がないとは限りません。ある会社の二つの部署AとBのエンゲージメントスコアを比較する場合を考えてみます。部署Aの95%信頼区間が[3.6, 4.0]で、部署Bの95%信頼区間が[3.9, 4.3]だったとします。これらの信頼区間は重なっていますが、統計的に有意な差がある可能性も否定できません[12]。
さらに、信頼水準を上げる(例えば、95%から99%)と、区間は広くなります。これは、より高い確実性を求めるほど、推定の精度が下がることを意味します。精度と確実性はトレードオフの関係にあります。
99%信頼区間は95%信頼区間よりも広くなりますが、真の値を含む確率は高くなります。例えば、ある組織サーベイで、95%信頼区間が[3.5, 4.0]、99%信頼区間が[3.4, 4.1]だったとします。99%信頼区間の方が幅は広いのですが、真の平均値を含む確率は高くなります。
他にも、サンプルサイズが大きくなれば、信頼区間は狭くなります。これは推定の精度が向上することを意味します。サンプルサイズが大きいほど、母集団の特性をより正確に反映し得るため、推定の不確実性が減少し、信頼区間が狭くなるということです。
脚注
[2] よくある誤りとして「今回のサーベイで示された95%信頼区間の範囲内に、真の値が95%の確率で含まれる」という説明があります。信頼区間は、サーベイでデータを取得した時点で範囲が定まり、また真の値は、具体的な値は不明ながらも何らかの得点に定まっていると想定しています。そのため、「サーベイでデータを取得した時点で、その信頼区間が真の値を含むか否か確定している」状況であり、それに対して95%と確率を述べるのは不適切だと言うことです。
この誤りは、当選確率1%の宝くじを購入し、それが外れた抽選結果がすでに出ている状況で「この宝くじは今現在、当選確率が1%だ」ということと似ており、すでに確定している結果に対してこのように述べるのは正しくないとおわかりいただけるでしょう。加えて、「100個中95個の信頼区間が、真の値を含む」という図の説明からもわかるように、信頼水準が表すのは確率でなく、複数回同様のサーベイを実施した仮定の中で算出される「割合」であり、95%の「確率」ということも不適切だと言えます。
[3] 正規分布の特性として、平均、中央値、最頻値が一致します。これによって、データの代表値を一意に定められます。また、標準偏差によってデータのばらつきを定量化できます。
[4] 例えば、ある指標の標準偏差が10で、サンプルサイズが100の場合、標準誤差は10/√100=1となります。サンプルサイズを400に増やすと、標準誤差は10/√400=0.5となり、半分になります。
[5] 中心極限定理とは別の性質として、母集団において注目している変数(指標)が正規分布している場合は、標本分布も正規分布になります。
[6] 例えば、サイコロを振る結果は離散的で一様分布ですが、多数振った平均値の分布は正規分布に近づきます。同様に、二値データの平均や、極端に歪んだ分布からのサンプル平均も、サンプルサイズが十分に大きければ正規分布に近づきます。
[7] サンプル平均と母集団の平均の関係について、正規分布の性質を利用しています。標準正規分布では、平均を中心に±1標準偏差の範囲に約68%のデータが、±2標準偏差の範囲に約95%のデータが含まれます。サンプル平均の分布も正規分布に従うため、同様の性質を持ちます。ここにおける標準偏差は標準誤差を指し、サンプル平均が真の平均からどの程度ばらつくかを示しています。
[8] 信頼水準の決定は、調査や分析の目的、必要な精度、および慣習を考慮して行います。通常、95%や99%が用いられますが、これは慣習や解釈のしやすさによるものです。95%は多くの場合で十分な信頼性を提供し、かつ実用的な区間幅を得られるため広く使用されています。より高い確実性が必要な場合は99%を選択しますが、区間が広くなるというトレードオフがあります。
[9] zスコアは、標準正規分布において、中心から左右に何標準偏差離れた点までの面積が目的の確率に等しくなるかを示します。例えば、95%信頼区間のzスコア1.96は、標準正規分布で中心から左右に1.96標準偏差離れた点の間に95%の面積(確率)が含まれることを意味します。
[10] 中心極限定理は、サンプルサイズが大きくなるほどサンプル平均の分布が正規分布に近づき、そのばらつきが小さくなることを表しています。サンプル平均の標準偏差(標準誤差)は、母集団の標準偏差を√n(nはサンプルサイズ)で割った値に近づきます。これは、サンプルサイズが大きくなるほど、サンプル平均が母集団の平均に近づくことを意味し、推定の精度が向上することを意味しています。
[11] 95%信頼区間は、同じ方法で多数調査を行った場合、その95%で真の値を含む区間が得られることを意味します。20回同じ調査を行えば、平均して19回は真の値を含む区間が得られますが、1回は真の値を含まない区間が得られる可能性があるということです。これは、統計的手法の性質上避けられない不確実性であり、結果の解釈時に考慮すべき点です。
[12] この現象は、信頼区間による検証が平均差の検定より厳しい計算になるためです。多少の制約がありますが、この問題を考慮して平均差の検定結果に合うよう区間計算を調整したガブリエル比較区間と呼ばれるものもあり、そちらでは区間の重なりによる有意性判断と平均差検定の判断が一致します。
執筆者
 伊達 洋駆 株式会社ビジネスリサーチラボ 代表取締役
伊達 洋駆 株式会社ビジネスリサーチラボ 代表取締役
神戸大学大学院経営学研究科 博士前期課程修了。修士(経営学)。2009年にLLPビジネスリサーチラボ、2011年に株式会社ビジネスリサーチラボを創業。以降、組織・人事領域を中心に、民間企業を対象にした調査・コンサルティング事業を展開。研究知と実践知の両方を活用した「アカデミックリサーチ」をコンセプトに、組織サーベイや人事データ分析のサービスを提供している。著書に『60分でわかる!心理的安全性 超入門』(技術評論社)や『現場でよくある課題への処方箋 人と組織の行動科学』(すばる舎)、『越境学習入門 組織を強くする「冒険人材」の育て方』(共著;日本能率協会マネジメントセンター)などがある。2022年に「日本の人事部 HRアワード2022」書籍部門 最優秀賞を受賞。東京大学大学院情報学環 特任研究員を兼務。
 能渡 真澄 株式会社ビジネスリサーチラボ チーフフェロー
能渡 真澄 株式会社ビジネスリサーチラボ チーフフェロー
信州大学人文学部卒業、信州大学大学院人文科学研究科修士課程修了。修士(文学)。価値観の多様化が進む現代における個人のアイデンティティや自己意識の在り方を、他者との相互作用や対人関係の変容から明らかにする理論研究や実証研究を行っている。高いデータ解析技術を有しており、通常では捉えることが困難な、様々なデータの背後にある特徴や関係性を分析・可視化し、その実態を把握する支援を行っている。