2024年9月20日
調整効果とは何か 影響指標の影響力を変える要因の検証
データ分析を駆使すれば、組織のありたい姿を捉えた成果指標に対して、その要因となる影響指標は何かを検討することができます。成果指標に対して、どの影響指標が有効なのかを検討する分析として有名なのが、回帰分析です。
本コラムで紹介する分析は、回帰分析の基本を知っていることを前提にしているため、ご存じない方は下記のコラムを先にご覧ください。
回帰分析を使えば、「ある成果指標に対して影響指標が関連していると言えるか」の関連の有無と、「それらはどの程度関連しているか」の関連の強度を検証することができます。
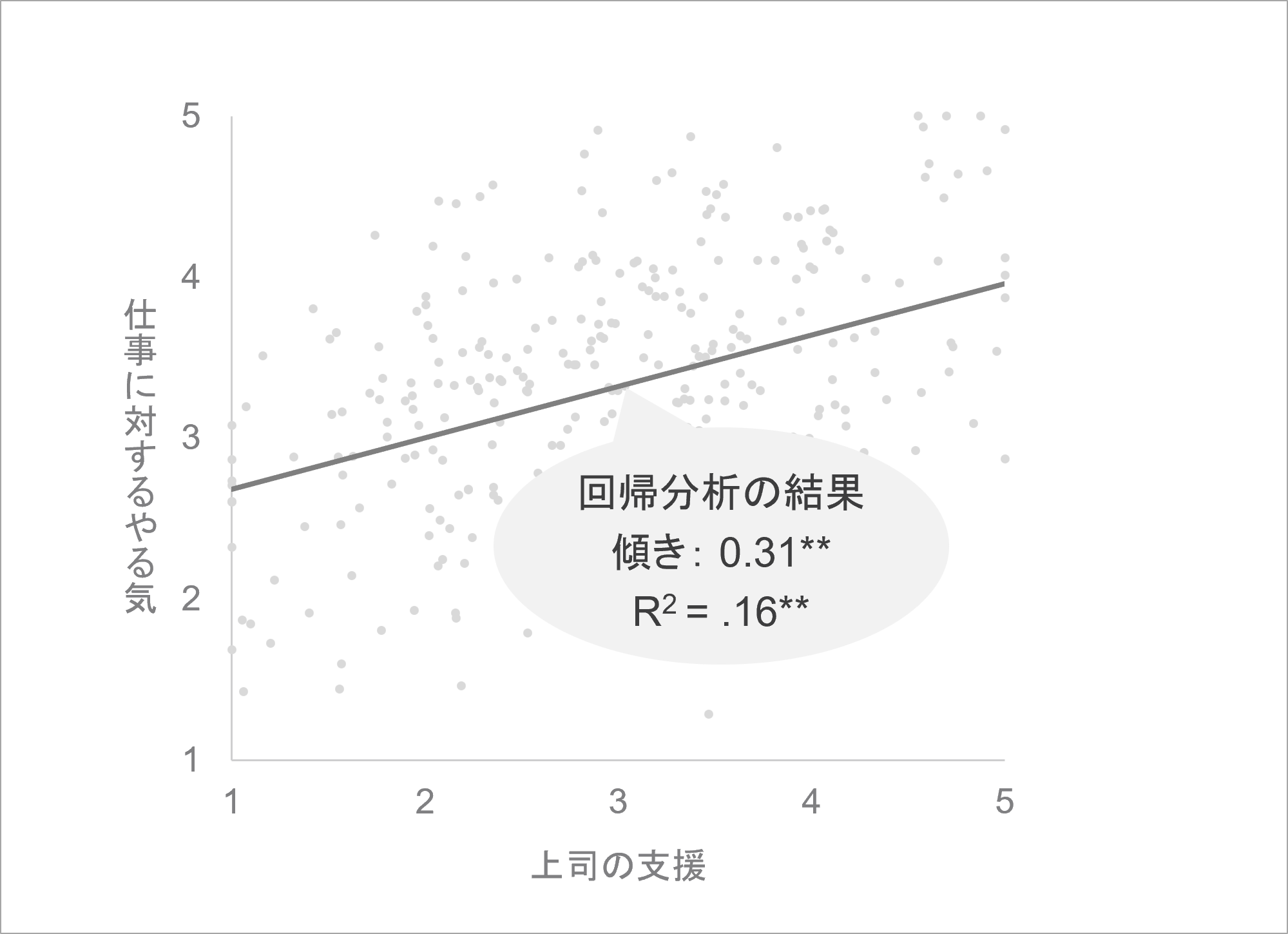
架空の例ですが、「上司の支援が部下の仕事に対するやる気を高めるか」を回帰分析で検討すると、以下のグラフのような結果が得られます。
回帰分析では、上司の支援と仕事に対するやる気の回答データの分布を表す散布図に対して、関連の傾向を表す直線グラフ(回帰直線)を考えることで2指標の関連性を検証し、数値で結果を示します。
この結果では、傾きにおいて「上司の支援が高いと、仕事に対するやる気も高い」ことが統計的に有意だと示されており、上司の支援が多い従業員は仕事のやる気が高い傾向があると把握できます。
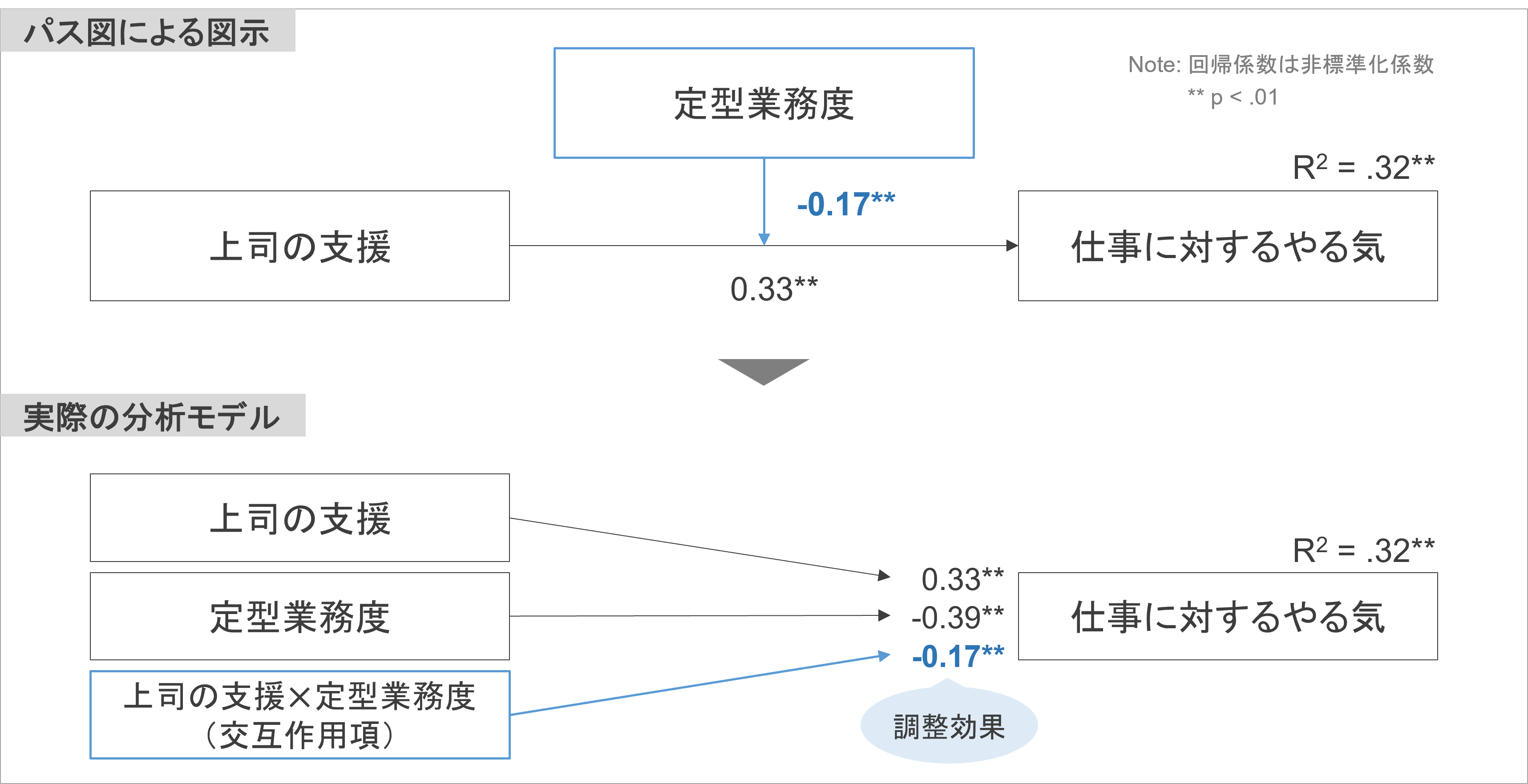
指標間の影響プロセスを示すパス図でこの関連性を描くと、下記の単純な図となります。
矢印につく数値は回帰直線の傾き(回帰係数)を表します。また、本コラムの内容との関連は薄いですが、回帰分析で重要な指標として、成果指標右上にある数値R2は決定係数を表します。
このように、回帰分析をすれば、「上司の支援が多くなると、仕事に対するやる気はどの程度高まるか」の平均的な傾向が検証できるわけです。
調整効果:影響指標の影響力を変える効果
回帰分析では、指標間の平均的な関連性・影響力を検証できます。
これに対して、「影響指標と成果指標の関連性を変える」ような、他の指標の存在を考えることができます。
例えば、先ほどの上司の支援と仕事のやる気の関連では、「上司の支援は、慣れきった定型業務だとむしろ作業の邪魔になりそうで、やる気を高める効果は少なさそうだ。つまり、普段の仕事が定型業務であるほど、上司の支援によってやる気が高まる効果は小さいのでは」と考えられるかもしれません。
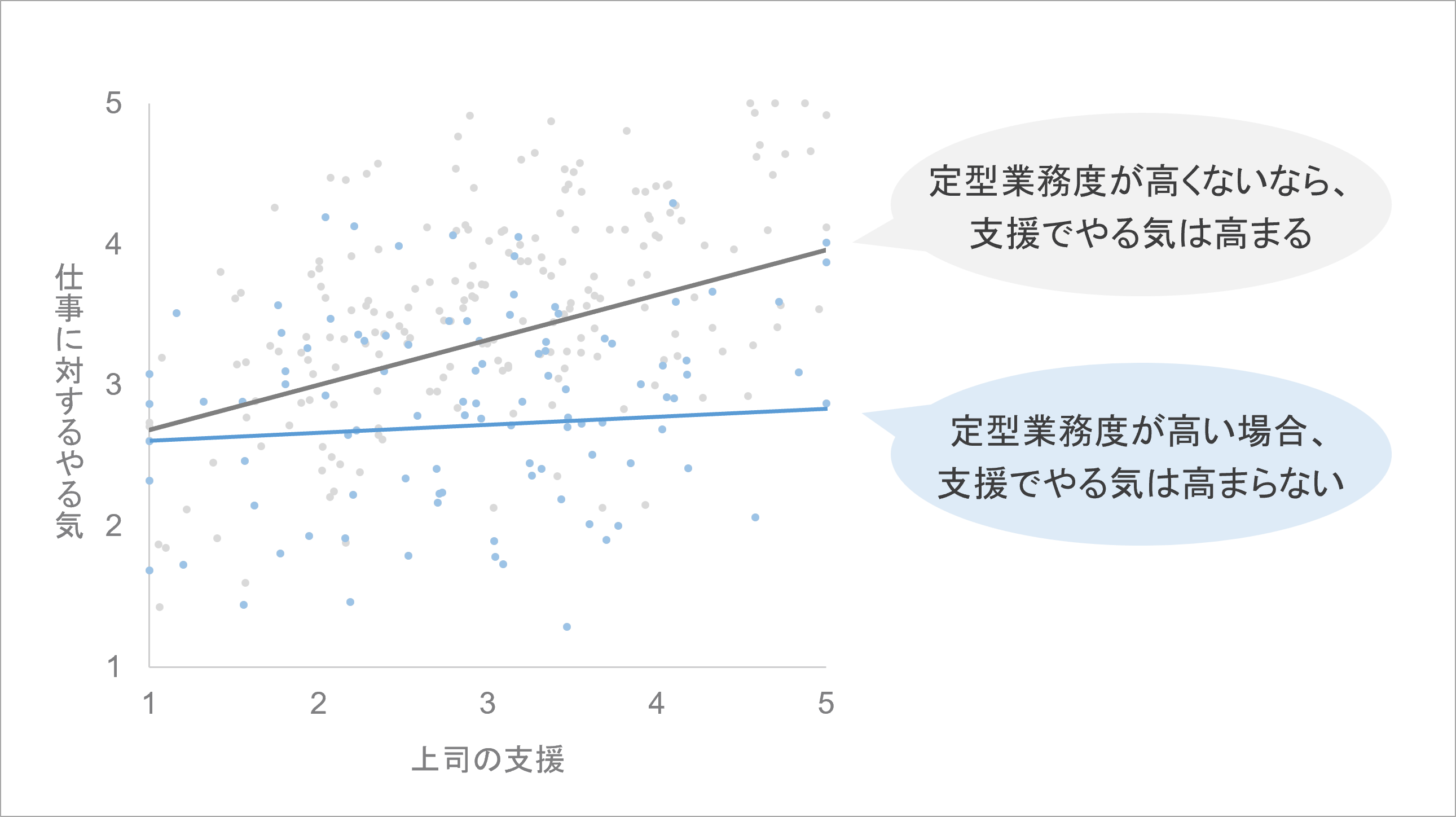
つまり、先ほど示したグラフを細かく見ると、以下のような状態になっている可能性が考えられます。
定型業務度を考慮しないもともとの分析では、上司の支援の高さに応じて仕事のやる気も高くなっている関連があります。
これに対して、定型業務度が高い場合、上司の支援が高くても仕事のやる気が高まっていない状態となっています。
このように、定型業務度を考慮して検証すると、最初に示された上司の支援が仕事のやる気に及ぼす関連が、定型業務度の高さによって違ってくることが見えてきます。
この考え方のポイントは、「仕事の定型業務度が高いほど、やる気が高まる/低くなる」といった、定型業務度がやる気の高低に及ぼす直接の影響について考えていないことです。
「仕事が定型業務であるほど、上司の支援(影響指標)が仕事のやる気(成果指標)に及ぼす影響が小さくなる」と、影響指標が成果指標に及ぼす影響力が定型業務度で変わることについて考えています。
このような、「影響指標と成果指標の関連性の強さ」あるいは「ある影響指標が成果指標に及ぼす影響の強さ」を変える効果のことを、統計学では調整効果(moderating effect)と呼びます。
また、先の例で上司の支援→仕事のやる気の影響力を変える指標として取り上げていた定型業務度を、調整効果を生む指標ということで調整変数(moderator)と呼びます。
ちなみに、上司の支援→仕事のやる気のような、影響指標が成果指標に及ぼす直接の影響は主効果(main effect)と呼び、調整効果とは区別されます。
先の主効果のみ描かれていたパス図に調整変数・調整効果を加えると、下図のようになります。
調整効果の結果の見方
ここからは、データ分析で調整効果を検証する際の結果の見方を解説します。
調整効果を検証するには、ある成果指標に対して、影響指標と調整変数との関連を検証する重回帰分析を実施します。
なお、ここで取り上げられる影響指標・成果指標・調整変数はすべて、数値データとして処理された回答データ(例:あてはまらない=1~あてはまる=5)のような、データの値を数量的な情報として扱う量的変数を前提とします[1]。
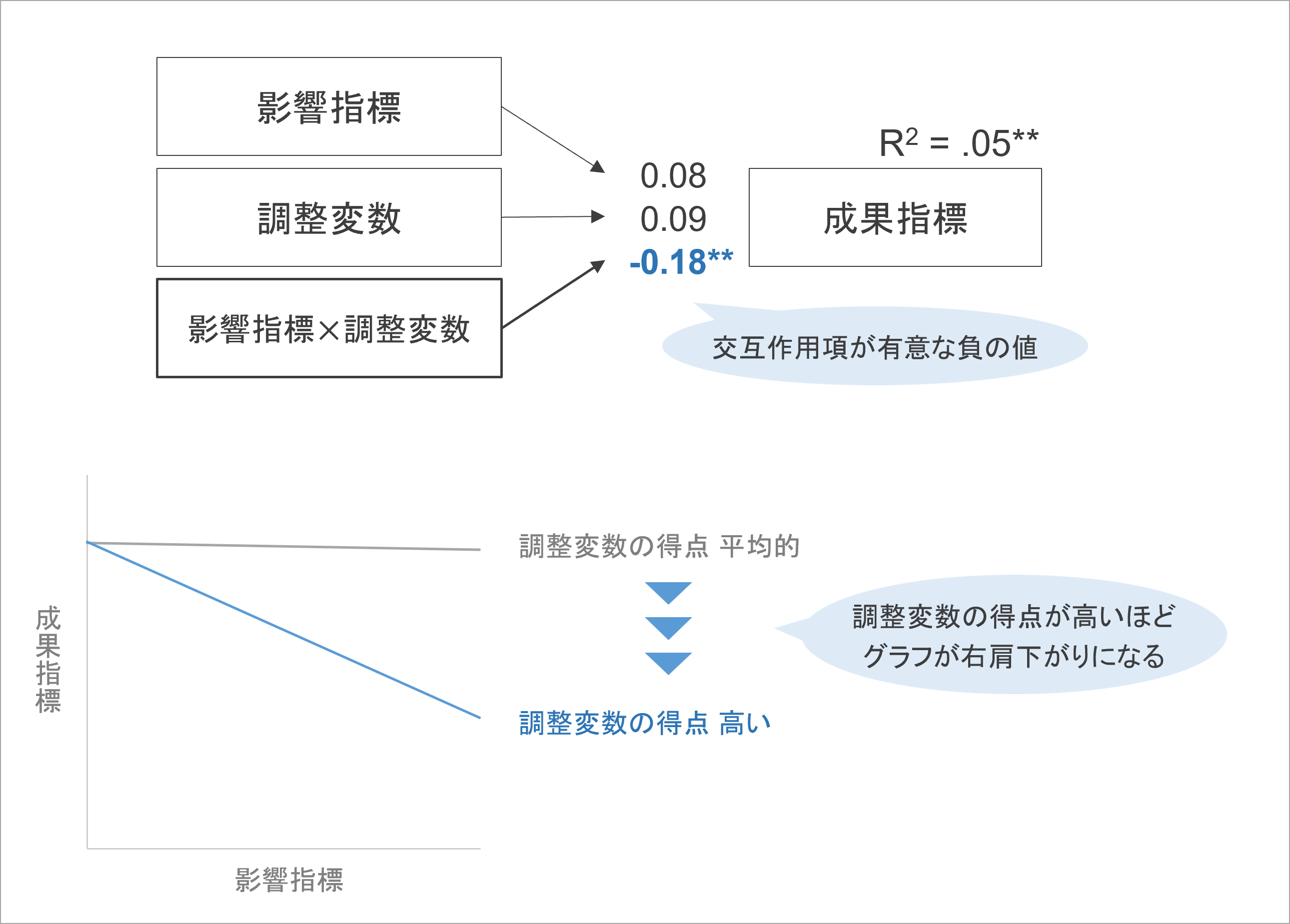
詳しくは割愛しますが、調整効果は影響指標と調整要因をかけ算した指標として示され、下図のような重回帰分析で検証されます。調整効果を表す影響指標と調整変数をかけ算した指標は「交互作用項」と呼ばれます。
交互作用項(調整効果)が統計的に有意か確認する
調整効果の検証で最初に確認するのは、「調整効果が統計的に有意か否か」です[2]。
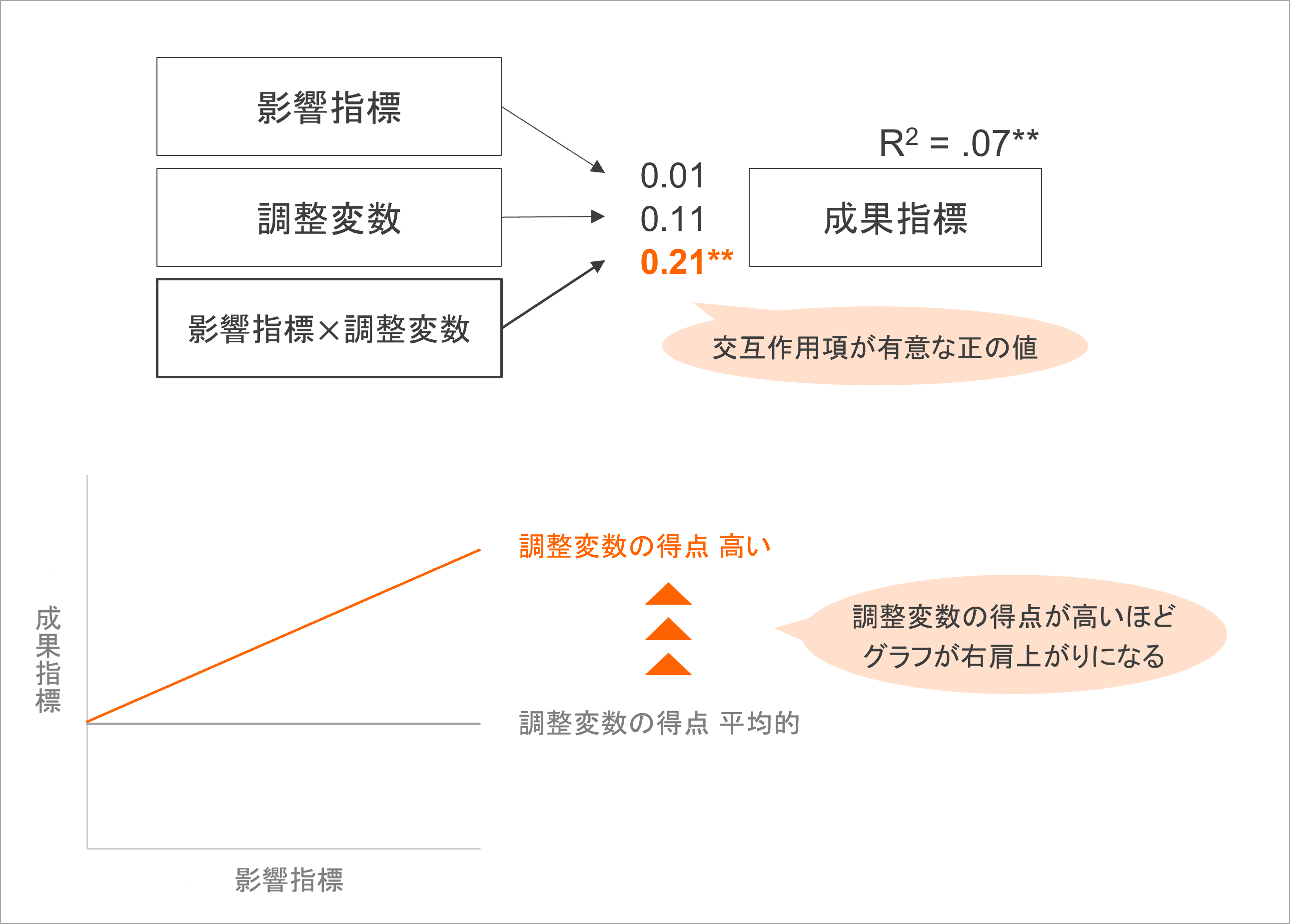
このような重回帰分析を実行すると、影響指標と調整要因の交互作用項についても回帰係数が推定され、それが統計的に有意か否かを普段の重回帰分析と同じ流れで確認できます[3]。そのとき、交互作用項が有意であったならば、「影響指標と成果指標の関連を調整要因が変える、調整効果がある」と考えられます。
調整効果が有意でないときは「取り上げた調整要因に、影響指標と成果指標の関連を変える効果はない」と判断できます。
交互作用項の回帰係数の正負を確認する
交互作用項の回帰係数の正負は調整効果の方向性を表すため、それを確認します。
交互作用項の回帰係数の正の値だったならば、それは「調整変数の値が高いと、影響指標と成果指標の関連がよりプラスの値になっていく」ことを表しています。関連がよりプラスになるということは、グラフの傾きが右肩上がりになっていくということです。
(見やすさのため、以降のグラフでは直線グラフの点プロットを割愛しています)
逆に、交互作用項の回帰係数が負の値だったならば、それは「調整変数の値が高いと、影響指標と成果指標の関連がよりマイナスの値になっていく」ことを表しています。関連がよりマイナスになるということは、グラフが右肩下がりになっていくということです。
このように、交互作用項の回帰係数の正負を見ることで、影響指標と成果指標の関連に対して調整効果がどのように表れているかを、大まかに把握できます。
調整変数の高低で、傾きを見比べる
回帰係数の正負による判断は「正ならば、調整変数の得点が高いほどより右肩上がりに、負ならばより右肩下がりになっていく」といった大まかなものです。「具体的に、調整変数の値に応じて影響指標と成果指標の関連はどう変わるのか」を捉えていません。
そこで、その具体的な関連を見るために、交互作用項が有意であることを確認した後に単純傾斜の検定(simple slope test)を行うことが一般的です。
この分析では、調整変数の平均とSD(標準偏差)を取り上げて、調整変数の得点が高い人を平均+1SD 、低い人を平均-1SDとして扱い、影響指標と成果指標の関連について回帰係数とその統計的有意性が高い人と低い人で異なるか検証して比較します[4]。
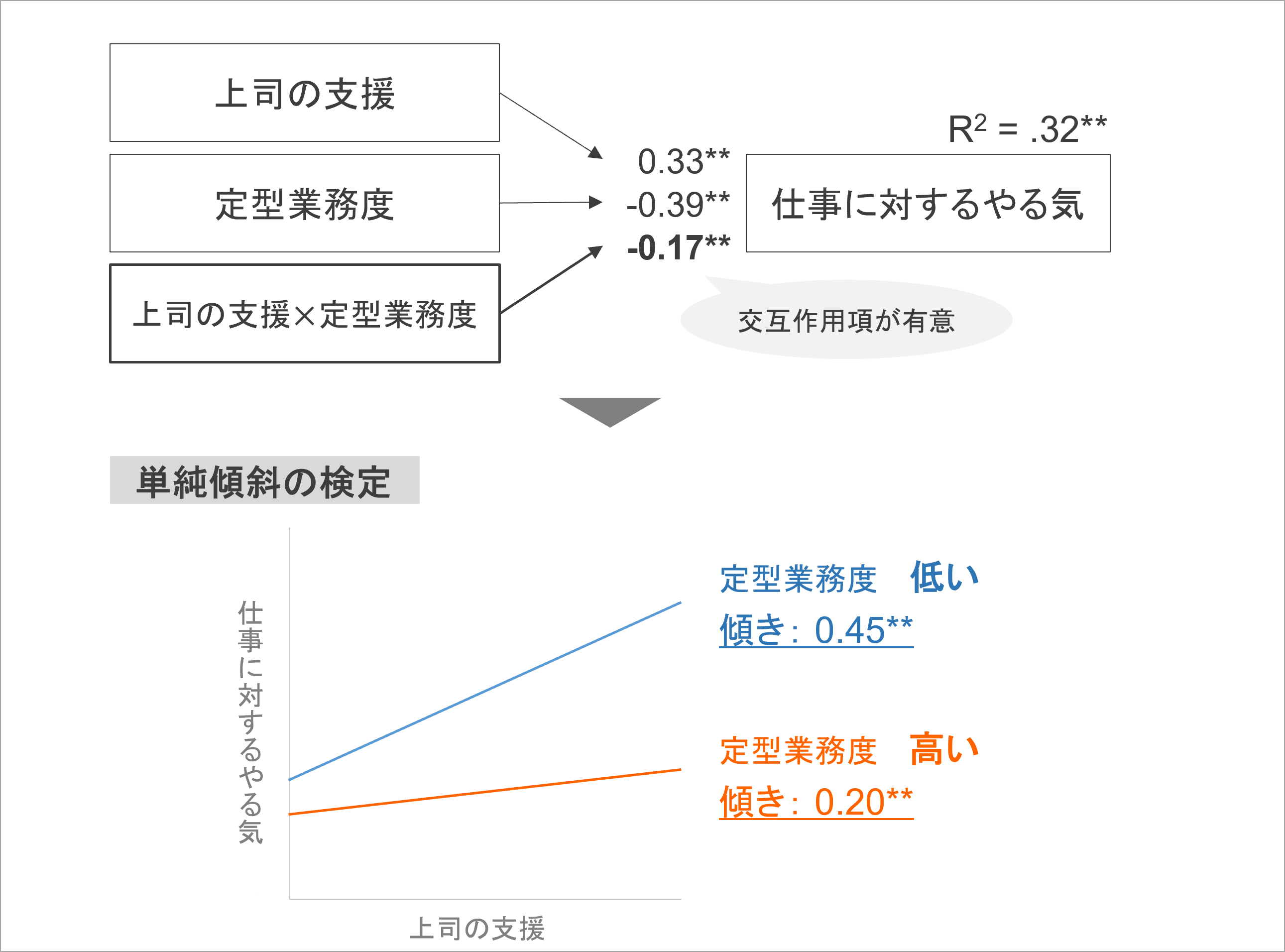
ここで、「上司の支援と仕事のやる気の関連を定型業務度が調整する」調整効果について検証した分析結果の架空例を見てみましょう。まず、調整効果の有無を交互作用項の回帰係数が有意であることを確認し、その後に単純傾斜の検定に進んでいます。
単純傾斜の検定では、調整変数の定型業務度が高い場合(平均+1SD)と低い場合(平均-1SD)で、上司の支援と仕事のやる気の回帰係数が統計的に有意か検証します。そこでは、上の図のように定型業務度が高い人/低い人の具体的な回帰係数の推定値がそれぞれ示されます。
定型業務度が低い青色の直線では、上司の支援と仕事のやる気は有意な正の関連(傾き0.45**)と示されています。その一方で、定型業務度が低い橙色の直線では、上司の支援と仕事のやる気は有意な正の関連が示されていますが(傾き0.20**)、グラフの傾きは定型業務度が低い場合と比べて上がり幅が浅いことが見て取れます。
この結果から、「上司の支援が仕事のやる気を高める傾向は、定型業務度が低い場合では強く見られるが、定型業務度が高い場合はその傾向が弱くなる」と解釈できます。
「定型業務度が高い場合は上司の支援の効果がなくなる」とまでは言えなくとも、定型業務度が高い場合は効果がいくらか弱まり、上司の支援がやる気を高める効果は小さくなりそうだと把握できるわけです。
調整効果を活かす分析アイデア
影響指標が成果指標に及ぼす影響・関連の強さを変える調整効果について考えることで、サーベイのデータ検証の幅を広げることができます。ここでは、調整効果の検証を活かした3つの分析アイデアについて紹介していきます。
なお、以降に示す分析結果例もすべて架空例であり、実際にデータを測定・分析した結果でない点はご留意ください。
対策がより有効に働く/あるいは効きが悪い従業員の特徴を分析する
組織サーベイの結果から対策を考えていく際、「その対策が特にヒットする従業員はどういった特徴があるだろうか」と気になることがあるでしょう。これに対して、調整効果の検証が役立ちます。
例えば、「外向的な性格の従業員は、組織内の対話を増やす対策案の効果がよりヒットする」と仮説があれば、下記の内容をサーベイで測定します。
- 影響指標:組織内対話の量
- 成果指標:(組織内対話によって改善したい指標)
- 調整変数:外向的な性格
その上で、組織内の対話と成果指標の関連を検証する際に、外向的な性格を調整変数として加えて調整効果を検証すれば、「組織内の対話と成果指標の関連は、外向的な性格の強さによって異なるか」を把握できます。
あるいは、これまで挙げてきた例「上司の支援が仕事のやる気を高める関連は、定型業務度が高いとなくなる」パターンは、上記の検証とは逆に、対策の効きが悪くなる仮説を検証するアプローチに該当します。ある対策が他の要因(調整変数)によって成果指標と関連しなくなるということは、対策が調整変数によって有効に機能しなくなる可能性を表します。
調整効果は、このような対策の有効性を変えうる要因の検証に使うことができます。
ネガティブな影響を持つ影響指標に対策する要因を探る
「業務負荷の多さにより離職が増加しているが、業務負荷を減らす施策は実施が難しい。この状況で、離職を抑える対策はどうするか」といったお悩みがあるかもしれません。これについても、調整効果の検証が有効です。
例えば、上記のお悩みについて「仕事について周囲に相談できる従業員は、業務負荷が多くても離職しようとはしない」と仮説を考えたとしたとき、下記の指標をそれぞれサーベイで測定します。
- 影響指標:業務負荷の実感
- 成果指標:離職意思
- 調整変数:業務相談機会の多さ
そして、業務負荷と離職意思の関連検証に業務相談機会の多さを調整変数として加えて調整効果を検証すれば、「業務相談機会が多いことで、業務負荷と離職意思の関連を弱められるか」を検証できます。下記の実証結果から、「業務相談機会を増やせば業務負荷と離職意思の関連が弱まると考えられ、まずは業務相談できる環境整備を対策とする」と方針を立てることができます。
なお、このアプローチは「ネガティブな影響指標そのものを減らしているわけではない」点に注意が必要です。上の例でいえば「相談機会が多いことで、業務負荷それ自体が減っている」わけではないということです。
当然ながら、ネガティブな影響指標はできるだけそれ自体を減らし抑制するのが望ましいです。このアプローチを考える際は、「調整効果による悪影響の抑制は、従業員にとってベストな選択肢でない」可能性が高いことを念頭に置き、ネガティブな影響要因を軽視しないよう意識すべきでしょう。
ある仕事が合っている/合っていない従業員の特徴を分析する
「関係者との交渉業務が多いこの仕事が合っている従業員は、どんな特徴があるだろうか」といった疑問についても、調整効果の検証が使えます。
例えば、「合理的思考力が高い従業員は、交渉業務が多い仕事に合っているのでは」と仮説を考えたとすれば、下記の指標をサーベイで測定します。
- 影響指標:普段の業務において交渉業務を行っている程度
- 成果指標:仕事へのやる気やパフォーマンスへの自信など、仕事へのポジティブな態度
- 調整変数:合理的思考力
そして、交渉業務を行っている程度と成果指標の関連について、合理的思考力で有意な正の調整効果(交互作用項の回帰係数)が認められ、単純傾斜の検定でも合理的思考力が+1SDと高い従業員で有意な正の関連が認められていたとしたら、合理的思考力の高い従業員は交渉業務が多い仕事が合っていると判断できます。
解釈は少し複雑ですが、上記の正の有意な調整効果は、「”交渉業務が多い仕事であると仕事に対するやる気やパフォーマンスへの自信が高い関連”は、合理的思考力が高い従業員ほどその関連傾向が強くなる」ことを表しています。
したがって、「合理的思考力が高い従業員であると、交渉業務が多い仕事でよりやる気や自信が高まる」と考えられるため、合理的思考力が高い従業員は交渉業務が合っていると言えるわけです。
このアプローチでは、調整効果がありそうな調整変数について様々な指標を取り上げることで、ある仕事に合っている従業員の特徴を広く検証することができます。例えば、合理的思考力以外に、「信念が強く頑固な従業員は、交渉業務が多い仕事が合っていない」と考えて頑固な性格を調整変数とした仮説を立てられるかもしれません。
調整効果を扱う際の注意点
調整効果を考慮してサーベイを設計・分析すれば、影響指標と成果指標の単純な関連性をさらに発展させて、個々の従業員や仕事の特徴を含めた分析を掘り下げることができます。
しかし、多くの可能性を詳細に分析できるからこそ、注意すべきポイントもあります。
ここからは、調整効果を扱ううえで特に注意すべき2点を紹介します。
調整効果は特に、仮説をしっかり立てて検証する
他の分析手法でも度々指摘していますが、データ分析では仮説が重要です。仮説がなく場当たり的に分析を繰り返して得られた結果は、そのサーベイで偶然示されただけのものを捉えている可能性が高まるためです。
調整効果は影響指標と調整変数をかけ算した指標を分析するわけですが、その気になれば、影響指標同士でかけ算した交互作用項をいくつも作成し、途轍もない個数の調整効果を検証することができてしまいます。それにより、そのデータのみで偶然得られる有意な調整効果を、分析を繰り返すことで取り上げてしまう可能性が出てくるのです。
調整効果は、特に仮説をしっかり立てて検証をすべきであり、分析時は仮説を立てた指標以外では調整効果を検証しないよう注意するのが良いでしょう。
影響指標と強く相関する指標は調整変数に使えない
調整変数として取り上げる指標で意識すべきこととして「影響指標との相関が弱い」ことがあります。まず、調整効果は重回帰分析の枠組みで分析を進めるため、相関が強い影響指標と調整変数を同時に含めると多重共線性[5]が出る可能性が高まります。そのため、影響指標と相関が強い指標を調整変数にするのは避けましょう。
調整効果について知ることで、回帰分析を用いた検証の幅を一気に広げられます。その一方で、調整効果は検証すべき事項も一気に増えるため、分析や解釈の手間が膨大になる難しさもあります。
注意点のひとつめ「仮説をしっかり立てる」ことを土台に検証事項を絞り込みつつ、主効果と区別される調整効果のメリットを最大限生かし、より各社にフィットしたデータ分析の展開を目指しましょう。
脚注
[1] データの入力方法を工夫すれば、量的なデータでないカテゴリカルな質的データ(研修参加/不参加や部署といった数量でないデータ(名義尺度)やいわゆる順序尺度のデータ)も、調整効果の検証は可能です。しかし、その手法は本コラムの解説レベルを超えた議論をいくつか含むため、ここでは説明を割愛して量的なデータに限定しています。
[2] 正確には、これよりも先に「決定係数が統計的に有意か否か」を確認します。調整効果を含んでいたとしても、この分析は重回帰分析の枠組みなため、調整効果を含むひとつひとつの回帰係数が統計的に有意かを確認する前にまず決定係数について統計的有意性を確認する必要があります。
[3] 調整効果の検証は重回帰分析の枠組みですが、重回帰分析でよく行われる「標準化偏回帰係数βで各指標の関連性の強さを比較する」ことをほぼやりません。この検証は「ある影響指標と成果指標の関連が調整変数で変わるか」に関心があり、種々の影響指標間の関連の強さ比較には関心がないためです。
[4] 調整効果の具体的検証は、下記文献で提案されたこの方法がもっとも有名ですが、これ以外にもいくつか検証方法があります。Aiken, L. S., & West, S. G. (1991). Multiple regression: Testing and interpreting interactions. Sage Publications, Inc.
[5] 多重共線性については、当社コラム「人事のためのデータ分析入門:回帰分析~要因を見出すための分析~(セミナーレポート)」で詳しく解説しています。
執筆者
 能渡 真澄
能渡 真澄
株式会社ビジネスリサーチラボ フェロー。信州大学人文学部卒業、信州大学大学院人文科学研究科修士課程修了。修士(文学)。価値観の多様化が進む現代における個人のアイデンティティや自己意識の在り方を、他者との相互作用や対人関係の変容から明らかにする理論研究や実証研究を行っている。高いデータ解析技術を有しており、通常では捉えることが困難な、様々なデータの背後にある特徴や関係性を分析・可視化し、その実態を把握する支援を行っている。