本コラムのテーマは「相関」です。「AとBは相関している」などの表現は、ビジネス界でも時々耳にします。これは一体何を意味しているのでしょうか。

本コラムでは「相関とは何か」と、「相関の注意点」の2点をお伝えします。

※本コラムは、2020年11月に開催したセミナー「人事のためのデータ分析入門：『相関』とは何か」の内容をもとに加筆・再構成したものです。

講師

伊達 洋駆　株式会社ビジネスリサーチラボ 代表取締役

神戸大学大学院経営学研究科 博士前期課程修了。修士（経営学）。2009年にLLPビジネスリサーチラボ、2011年に株式会社ビジネスリサーチラボを創業。以降、組織・人事領域を中心に、民間企業を対象にした調査・コンサルティング事業を展開。研究知と実践知の両方を活用した「アカデミックリサーチ」をコンセプトに、ピープルアナリティクスやエンゲージメントサーベイのサービスを提供している。著書に『オンライン採用 新時代と自社にフィットした人材の求め方』（日本能率協会マネジメントセンター）など。

「相関」とは何か

2つの指標の相関を明らかにする分析手法として「相関分析」があります。初めに、相関を分析することによって何が分かるのかを整理します。

相関を分析すると、2つの指標の関係性が分かります。例えば、身長と体重という指標があったとします。それらが「相関する」ことが示された場合、「身長が高いデータでは、 体重が重い」という関係にあります。

相関を分析する際には、「相関係数」を算出します。相関係数は、「2指標の関係の種類」と「2指標の関係の強さ」を表しています。

2指標の関係の種類とは、一方の指標の高さともう一方の得点の高さの対応に関する情報です。

例えば、xとyという2指標があったとします。xが高いときyが高い、あるいは、xが低いときyが低いという関係が成立する場合、これを「正の相関」と呼びます。

逆に、xが高いときyが低い、あるいは、xが低いときyが高いという関係もあります。これを「負の相関」と呼びます。

2指標の関係の強さとは、2指標の関係性がどの程度強いかに関する情報です。相関は、一方の値の大きさともう一方の値の大きさの関連について、強い相関や弱い相関といった形で、その関連の強さを評価できる性質を持っています。

相関係数の求め方

相関分析では、相関関係についての数値を求めて、その評価をします。ここでは、相関係数の計算方法を紹介します。これを学ぶことで、相関が意味することやその特徴を捉えることができます。

最初に、相関係数の式を示します。

相関係数の式自体は、文字式ばかりで理解が難しいかもしれません。ここでは少し掘り下げて、この式の意味するところを考えます。

まずは式の分子に注目してください。複雑な分子の計算式は、専門的には共分散というものを求める式になっています。相関係数の構成要素の一つに、共分散があるわけです。

共分散は、2指標の関係を表しています。先ほど、相関は2指標の関係を表すことを説明しましたが、この「2指標の関係性を表す」という特徴は、式に含まれる共分散が持つ特徴です。

共分散の式を言葉で置き換えると、分子の式は「（x-xの平均）×（y-yの平均）の総和÷データ数」となります。この式がどうして2指標の関係を表しているのか、これを理解することこそ、相関を理解するための重要なステップになります。

共分散：二つの指標間の関連の数量化

共分散の意味を理解する上で知っておくべき概念があります。それは「偏差」です。偏差とは、測定されたある指標のデータについて、回答者それぞれの回答値とそのデータの平均の差をとった値を指します。

例えば、4名から職務満足感のデータを測定して、60点、70点、70点、100点という回答値が得られたとします。このとき、4名の回答の平均は75点なので、4名の偏差はそれぞれ-15点、-5点、-5点、+25点となります。

共分散の式にも偏差が含まれています。「x－（xの平均値）」、これを「xの偏差」と呼びます。同様に、「y－（yの平均値）」を「yの偏差」と呼びます。この理解を踏まえて共分散の式を見返すと、2つの指標の偏差のデータをかけ算した計算を含んでいることがわかります。この部分こそ、共分散の考え方の真骨頂です。

共分散の式に2つのデータの偏差同士のかけ算（積）を入れる狙いは、散布図における各プロットの位置を考えると理解できます。ここではxとyという2つの指標を組み合わせて散布図を描く状況を考えてみましょう。

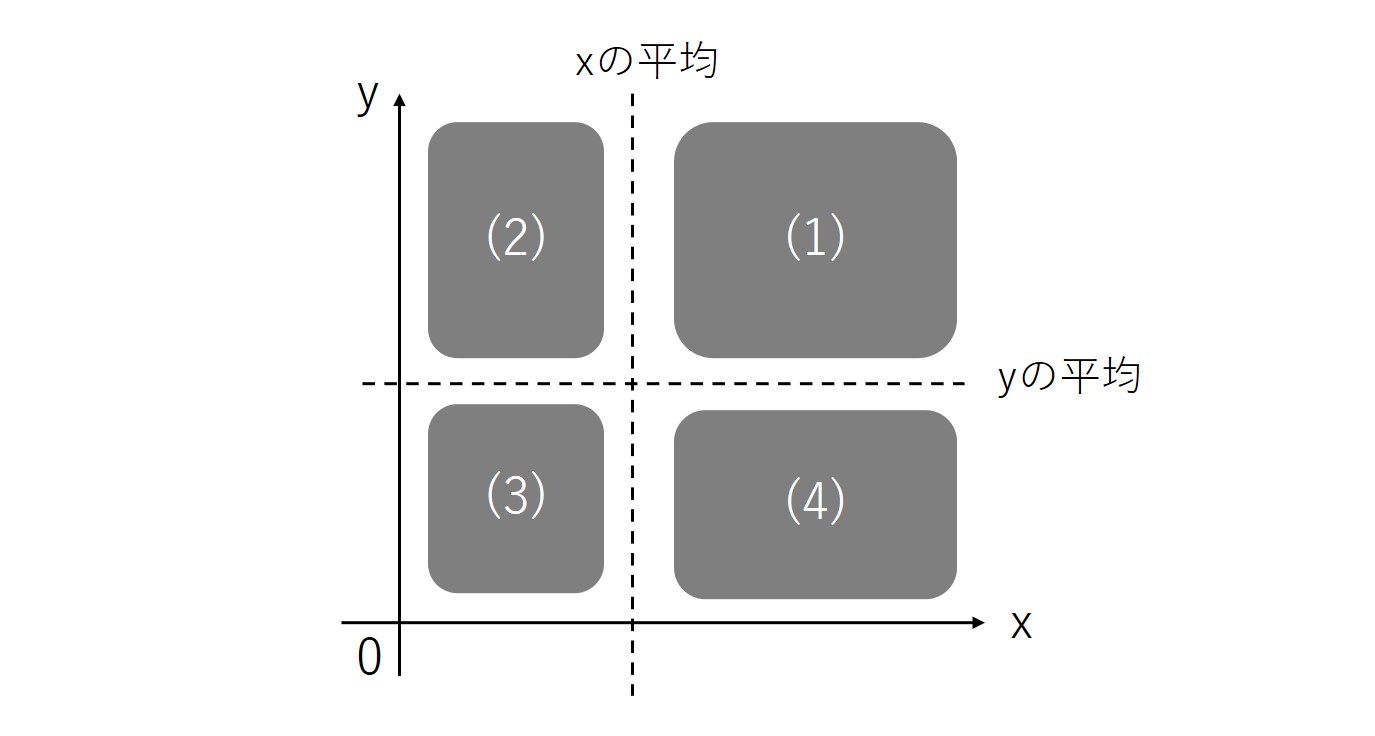
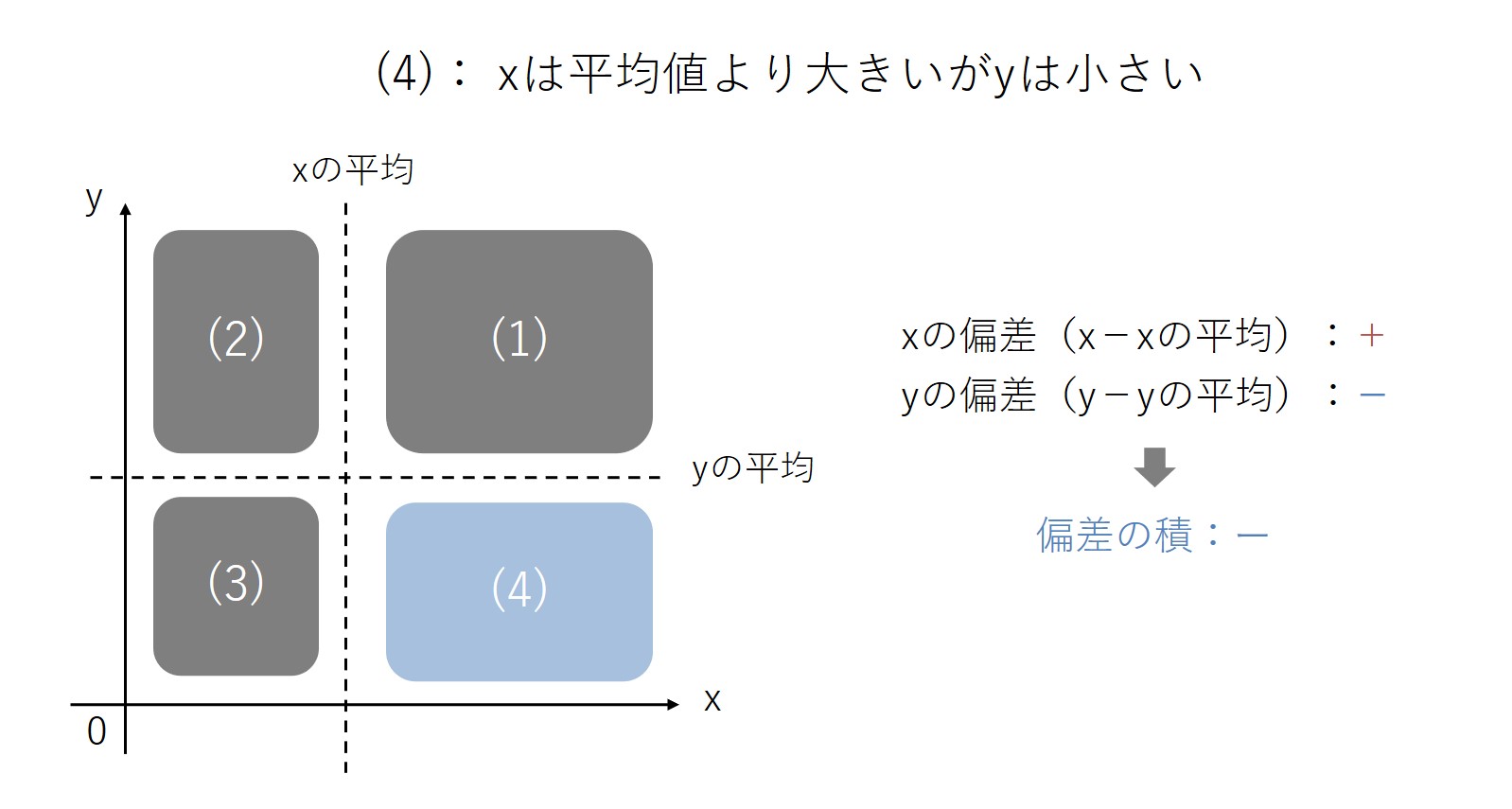
散布図にxの平均とyの平均を点線で書き込んでみます。すると、平均値を巡って4つの領域が出来上がります。

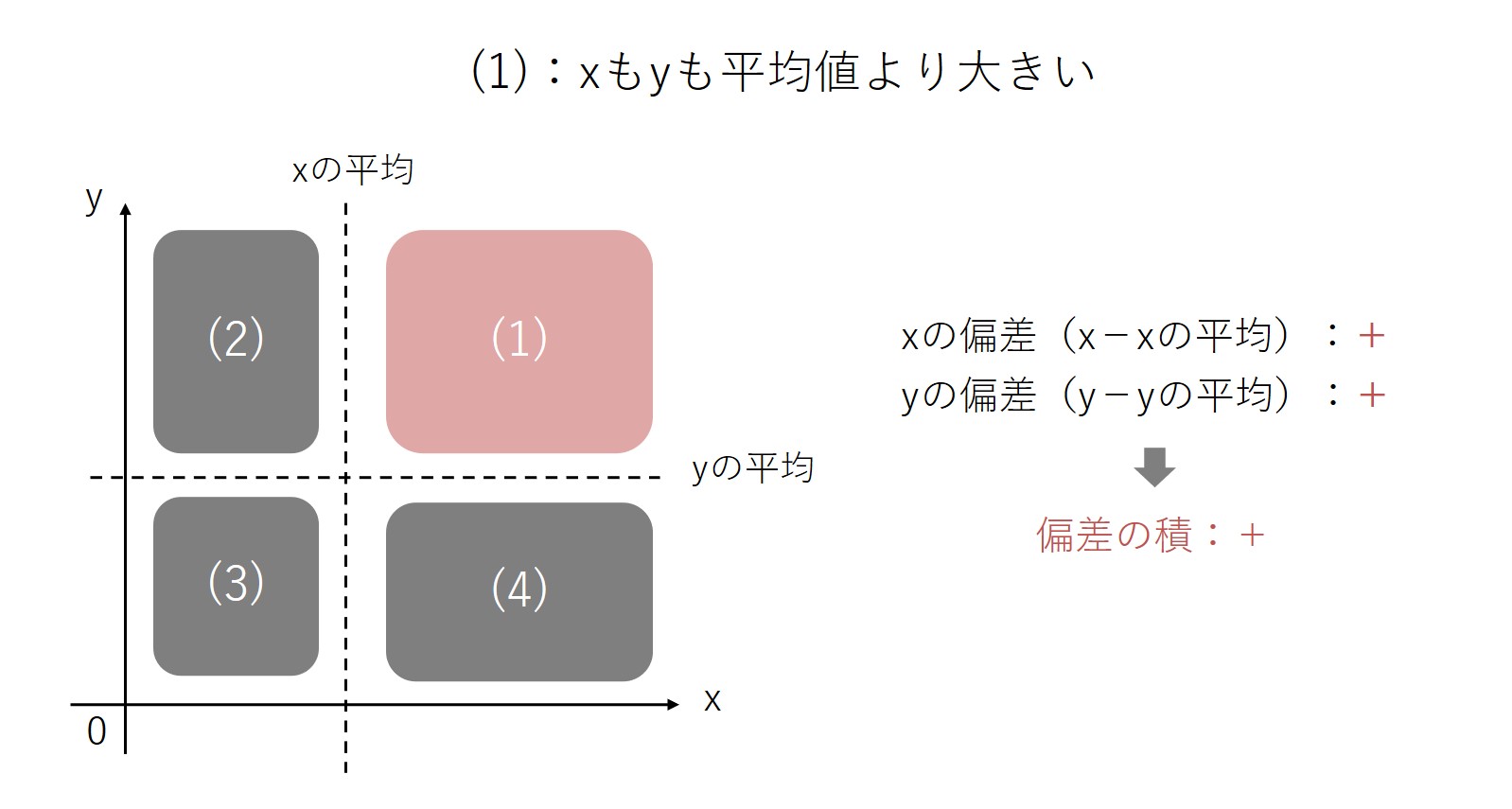
まず、右上の領域(1)について考えてみます。(1)の領域に入るプロットは、xとyのデータの両方が、それぞれの平均より大きい値となります。xとyのデータが両方とも平均より高い回答者は、(1)の領域のどこかにプロットされることになります。

ここで、(1)の領域における偏差を考えると、xについて、(1)ではxの平均よりも高いxの得点を持つデータが集まるため、x－（xの平均値）であるxの偏差は「プラス」になります。

同様にして、(1)ではy－（yの平均値）であるyの偏差も当然「プラス」になります。そうすると、xとyの偏差の積も「プラス」になります。(1)の領域に含まれるプロットは、偏差の積がプラスになるということです。

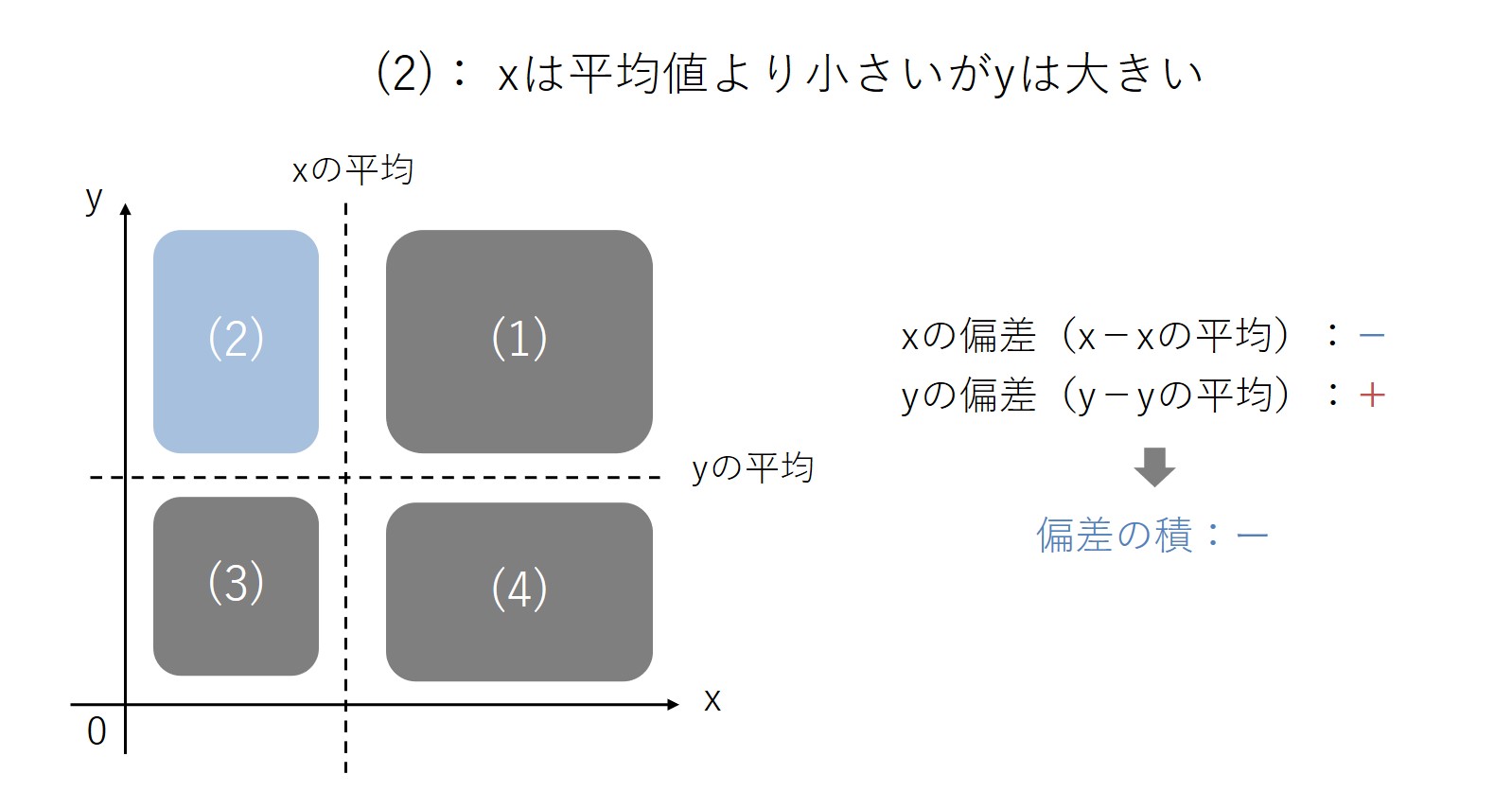
(2)の領域では、xは平均より小さく、yは平均より大きい回答者のプロットが入ります。

(1)と同じ方法で、(2)の領域における偏差を考えてみます。(2)の領域に入るプロットにおいて、xは平均より小さいので、xの偏差は「マイナス」になります。他方yについては、yの値は平均より大きいので、yの偏差は「プラス」になります。

xの偏差とyの偏差をかけ算した偏差の積は、マイナス×プラスで「マイナス」になります。(2)の領域に含まれるプロットについて、偏差の積はマイナスになるということです。

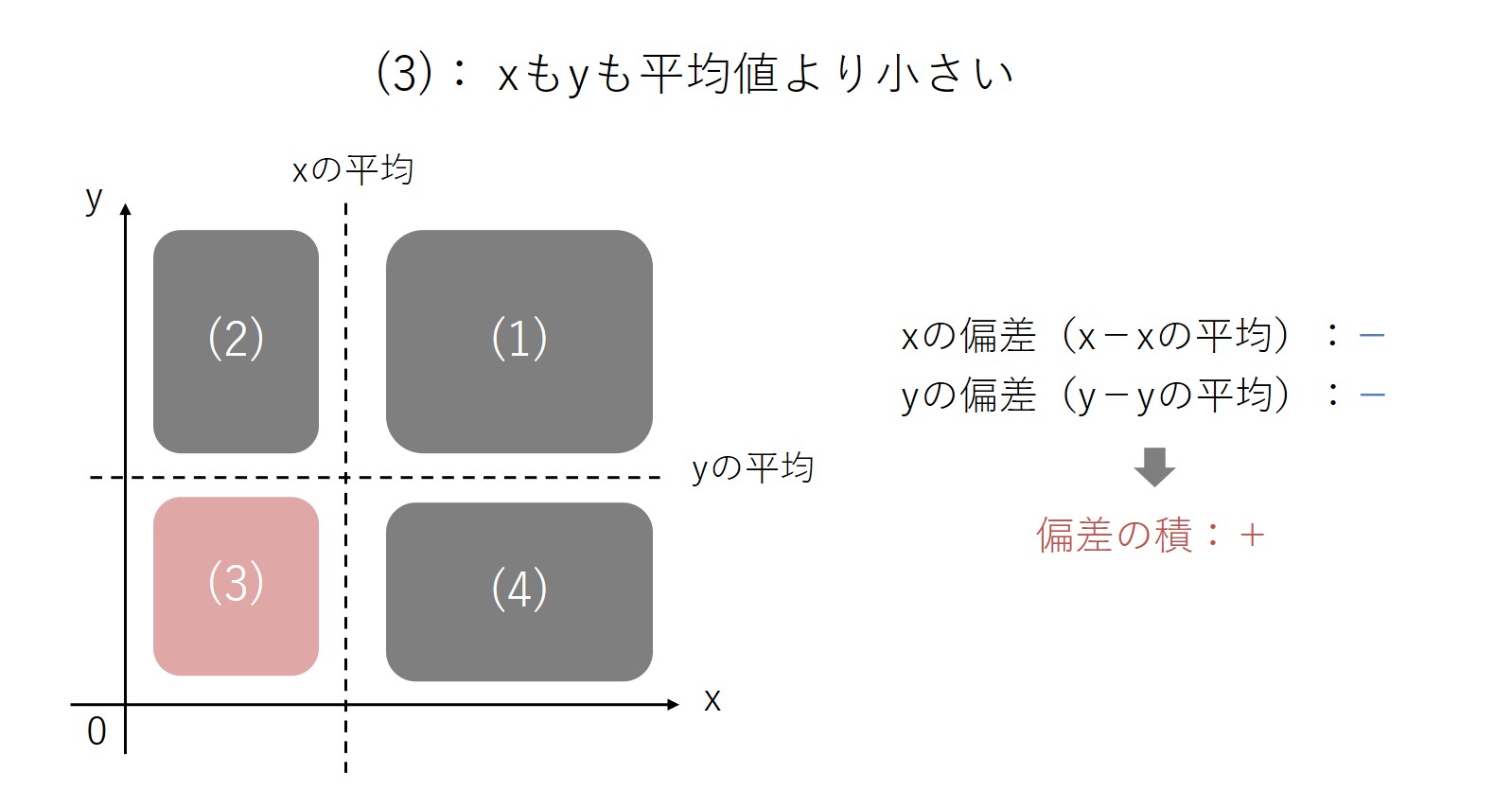
(3)の領域は、xもyも平均値より小さいプロットが入るゾーンになります。このゾーンでは、xもyも平均値より小さいので、xの偏差もyの偏差も「マイナス」になります。

そして偏差の積を求めると、マイナス×マイナスで「プラス」になります。(3)の領域に含まれるデータでは、偏差の積がプラスになります。

(4)の領域は、xは平均より大きく、yは平均より小さい領域です。xは平均より大きいので、xの偏差は「プラス」になります。一方、yは平均より小さいので、yの偏差は「マイナス」です。

この2つの偏差をかけ合わせると、偏差の積はプラス×マイナス＝「マイナス」になります。

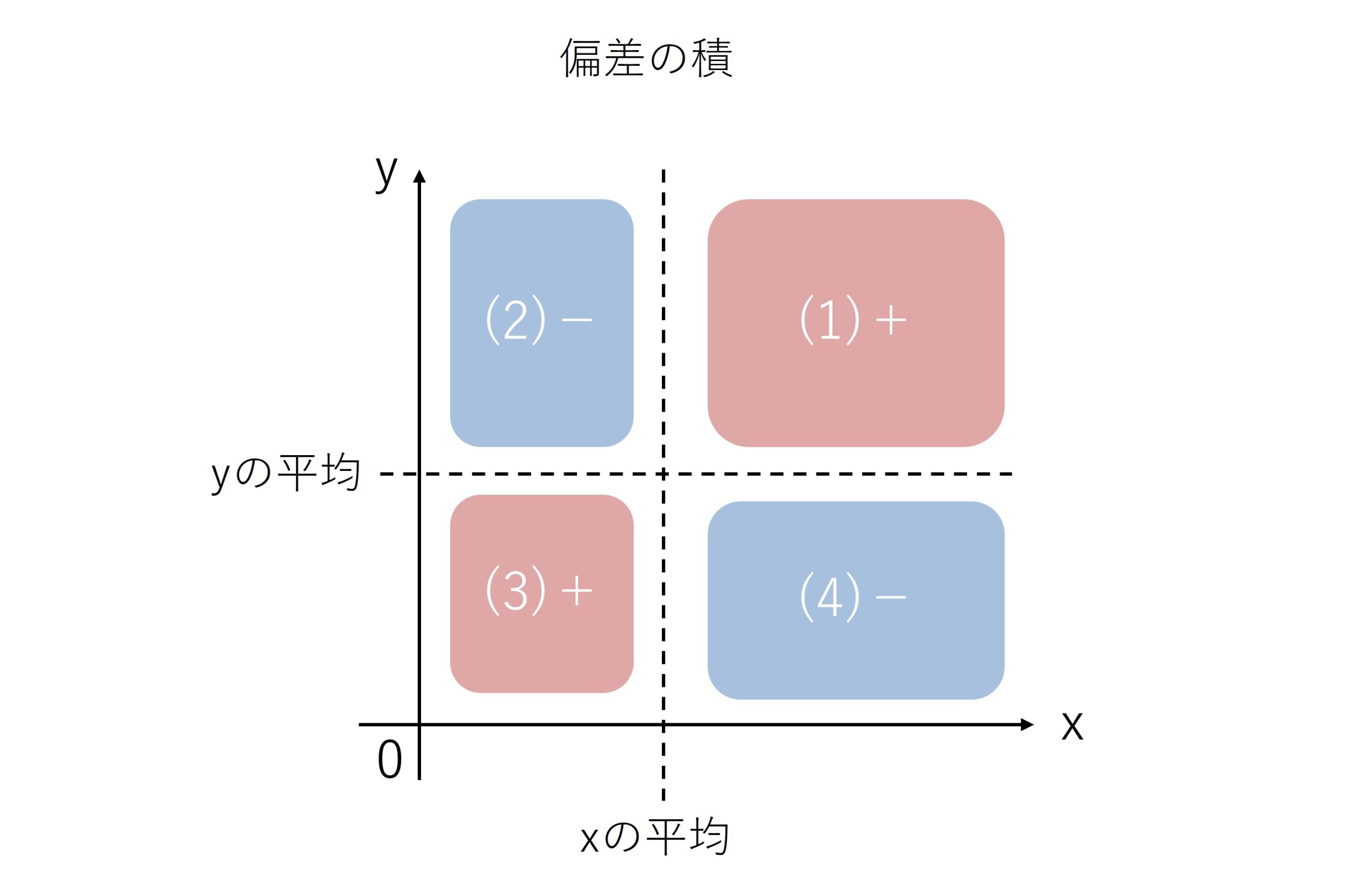
以上を踏まえて、4つの領域を見てみると、(1)・(3)に位置付けられるデータは偏差の積がプラスになります、一方、(2)と(4)に位置付けられるデータは、偏差の積がマイナスになります。

偏差の積にはこういった特徴があるわけです。

ここで、共分散の式「（偏差の積の総和）÷（データ数）」をもう一度思い出してください。

共分散の計算では、偏差の積を足し合わせていきます。このとき、散布図のプロットが(1)の領域と(3)の領域に多く含まれていると、偏差の積はどんどん加算されていくことになります。つまり、(1)と(3)に含まれていれば含まれているほど、偏差の積を足し合わせた値はプラスの方へ大きくなる傾向があります。

逆に、(2)と(4)に含まれるデータが増えていくと、偏差の積がマイナスのものが増えていくため、それらを足し合わせたものは、マイナスの方へとどんどん大きくなります。

さらに、(1)(2)(3)(4)すべての領域に、各プロットが等しくばらけていたとします。そうすると、偏差の積を足し合わせた際にプラスとマイナスが相殺されて、その合計はゼロに近づいていく特徴があります。

ここで、偏差の積を足し合わせた合計がプラスになっている状況を考えると、それは各データのプロットが(1)と(3)に集中している状況を意味します。それはすなわち、「xのデータが高いとき、yのデータは高い」、「xのデータが低いとき、yのデータは低い」状態を表しています。

同様に、偏差の積を足し合わせた合計がマイナスになっている状況を考えると、それは各プロットが(2)と(4)に集中している状況を意味しています。これは、「xのデータが高いとき、yのデータは低い」、「xのデータが低いとき、yのデータは高い」状態です。

そして、偏差の積を足し合わせた合計が0に近い状況を考えると、それは各プロットが(1)(2)(3)(4)すべての領域にまんべんなく散らばっている状況を意味しています。「xのデータの高低とyのデータの高低に関連は見られず、散布図がバラバラ」な状態です。

このように、偏差の積の合計は、その値の大きさが2指標の関連性の強さを表す情報を持つことになります。

上記のように、2指標の関係性は、(1)と(3)の領域に各データのプロットが入っているほど、プラスの関係性になりますが、これを「正」の関係性と呼びます。そして、(2)と(4)の領域にプロットが入っているほど、マイナスの関係性になり、これを「負」の関係性と呼びます。

しかし、偏差の積を合計した値には、関係性の指標として望ましくない性質があります。それは、データの数が増えるだけその値を合計して関係性を評価していくことです。

偏差の積の合計値は関連性の強さを表しますが、その値の大きさはデータの個数でも変わります。2指標の関係性を見る視点では、データの個数に依存せず関係性の程度を評価したいため、データの個数で関係性の指標が変わってしまうのは避けたいところです。

そこで、偏差の積の合計値をそのデータの個数で割り算することで対処が行われます。偏差の積の合計をデータ数で割ることで、関係性の指標としてより純粋なものに仕上げているわけです。

このような考え方を経て、共分散の式「（xの偏差）×（yの偏差）の総和÷データ数」が成り立ちます。関連性を意味するという性質を生かしつつ、データの個数が生み出す問題にも対処することで「2指標の関係性」を表す指標になっている、ということがご理解いただけたと思います。

ここで、実際の計算手順を追って、共分散の計算の流れを確認 してみましょう。

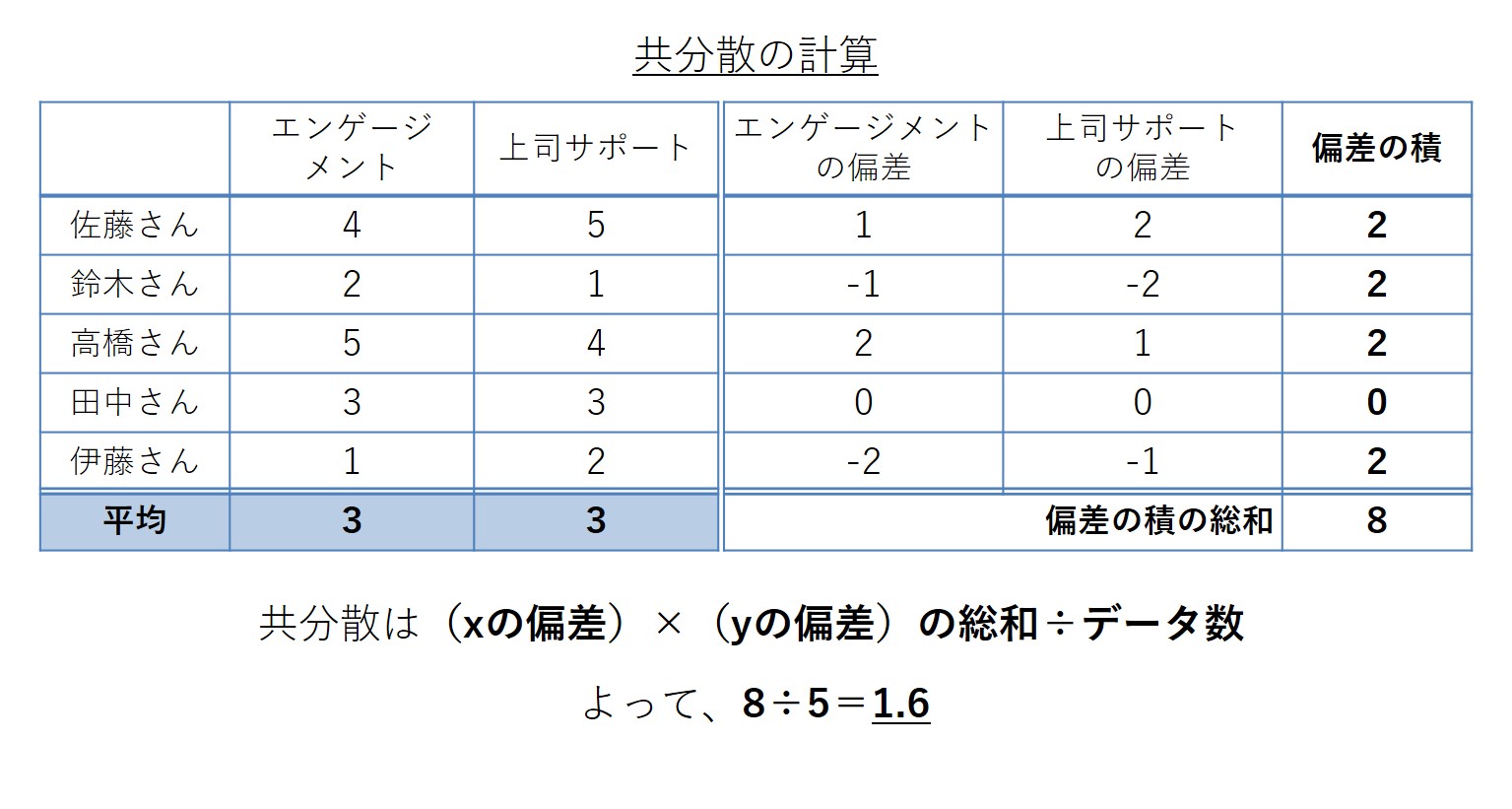
例えば、佐藤さん、鈴木さん、高橋さん、田中さん、伊藤さんという人が組織サーベイを受け、エンゲージメントと上司サポートについて回答したとします。佐藤さんは、エンゲージメントに4、上司サポートに5と付けました。鈴木さん以下も同じように、それぞれ自分の回答を付けました。このようなデータがあるとします。

エンゲージメントの平均は3、上司サポートの平均は3となっています。この場合に、佐藤さんの偏差は、4-3=1となります。また、佐藤さんの上司サポートの偏差は、5-3=2です。同じように、鈴木さん、高橋さん、田中さん、伊藤さんの4人についても、それぞれ偏差を計算します。

共分散の計算では、2指標の偏差の積をとることがポイントです。佐藤さんの場合、エンゲージメントの偏差が1、上司サポートの偏差が2なので、偏差の積は1×2=2となります。鈴木さんの偏差の積は、-1×-2=2。このように計算していきます。

高橋さん、田中さん、伊藤さんについても、偏差の積を導き出していきます。そうすると回答者全員分の偏差の積が求まります。それら全員の偏差の積を足すと、8という数字が出ます。偏差の積を「合計する(総和)」というのは、具体的にはこのような手続きになります。

最後に、偏差の積の総和を「データ数で割る」ことが必要です。今回、5人のデータがあるので、偏差の積の総和8を5で割ると8÷5=1.6になります。これが共分散の計算の内容です。

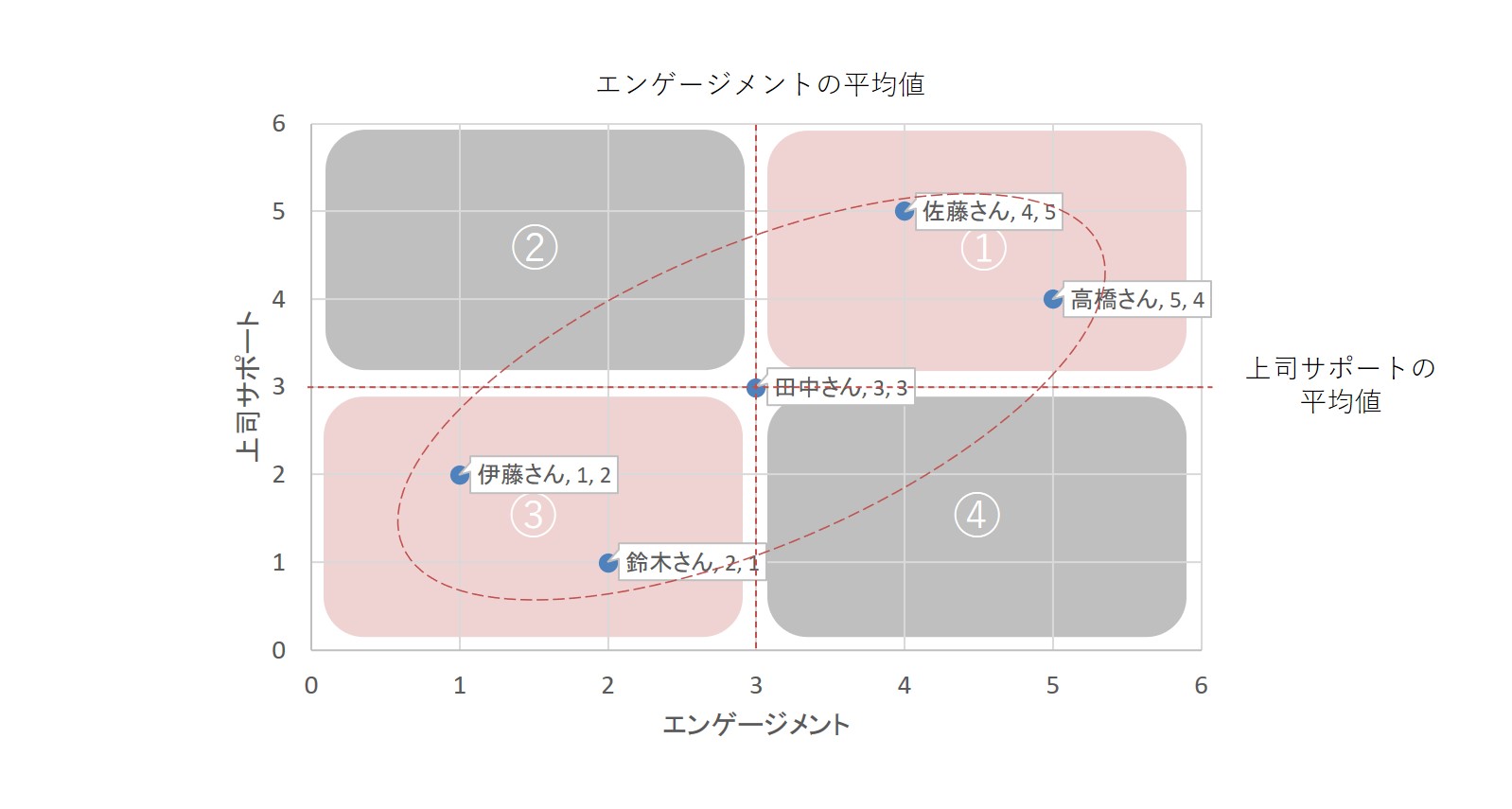
この例について、散布図を描いてその状態を確認してみましょう。

エンゲージメントと上司サポートについて、佐藤さんから伊藤さんまで、5人の数値を出しました。それを散布図で表したのが上図になります。(1)の領域と(3)の領域にプロットが多く入っています。先ほど計算した共分散の値が1.6とプラスの値でしたが、確かに、散布図の状態は(1)と(3)にプロットが集中した、全体的に右肩上がりの関連が見られることがわかります。

要するに、エンゲージメントと上司サポートについては、「エンゲージメントが高いとき上司サポートも高い、エンゲージメントが低いとき上司サポートも低い」という、プラスの関係＝正の関係にありそうだということが分かるわけです。

共分散の弱点：単位の影響を受ける

ただ、この共分散には弱点があります。それは、「取り上げた2指標の”単位”の影響を非常に大きく受けてしまう」ことです。

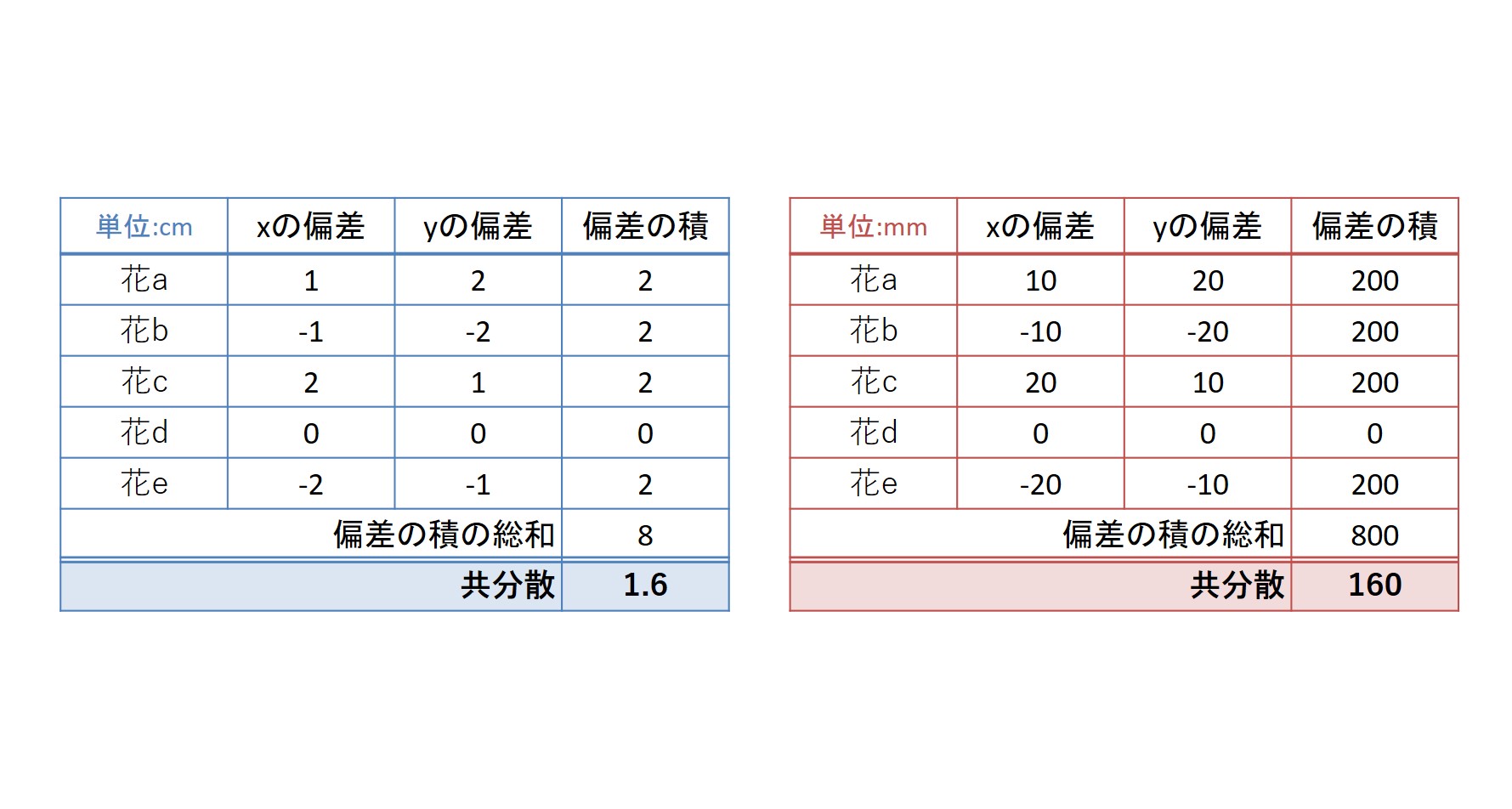
例えば、とある花の雄しべの長さ(x)と雌しべの長さ(y)の関係性を検討しようと思い、データを集めて共分散を計算したとします。ここで、あるグループでは雄しべの長さ(x)が1センチとしてデータをとりました。別のグループでは、同じ花から10ミリとしてデータをとったとします。

もちろん、1センチと10ミリはそれぞれ同じことを意味していますが、各グループで別々に共分散を計算していくと、後者のグループではデータに入力されるのが10という数値になるため、後者のグループで計算される共分散は大きな値になってしまうということが分かります。

左側はセンチメートルを単位にしたグループで共分散を算出したものです。右側は単位をミリメートルにしたグループで算出された共分散になります。センチメートルの場合の共分散は1.6に対し、ミリメートルの場合は160になっています。本来は1センチと10ミリというのは同じことを意味しているはずなのに、共分散の値はかなり違ってしまっています。

このように、単位による影響は大きなものです。共分散の値を出せたとしても、そこで表される関係性の程度が強いのか弱いのか、判断が難しくなります。

相関係数：単位の問題も解消した関係性の指標

共分散の弱点の対処法として考えられるのは、単位の概念がなくなるように変換をすることです。つまり、単位に依存せず関係性の強さを評価できるよう、変換していきます。この「単位の概念がなくなるような変換」を行っているのが、相関係数の分母にある数式です。

この複雑な分母の式は2指標それぞれの標準偏差をかけ算したものを表しています。「なぜ標準偏差の積を分母に置く(割り算する)と単位の概念がなくなるのか」という点については、議論が複雑で相関係数全体の理解を妨げてしまう恐れがあるので、本コラムでは説明を割愛します。

ただ、この分母の式が意味していることは理解していただきたいと思います。相関係数の式において、先に述べた通り、分子は共分散の式です。共分散は、2指標の関係性が正か負かというのは分かるけれども、関係の強さは単位の影響を受けてしまう問題がありました。

そこで、「単位の概念をなくしてその影響を除去する」ことを狙って、この分母における計算が加えられたわけです。単位の影響を除去する役割をこの分母が担っています。

言い方を変えると、相関係数というのは、共分散から単位の影響というのを取り除いたものです。共分散の性質がわかれば、相関が意味することも分かるというのは、このような背景があるからです。共分散から単位の影響を取り除けば、それは相関係数である、という話でした。

相関係数の特徴

相関係数の特徴は、まず、その値は-1から1の間の値を取るという特徴があります。どのような単位の変数であっても、分母できちんと共分散を割ることで、-1から1の間の値に収まります。

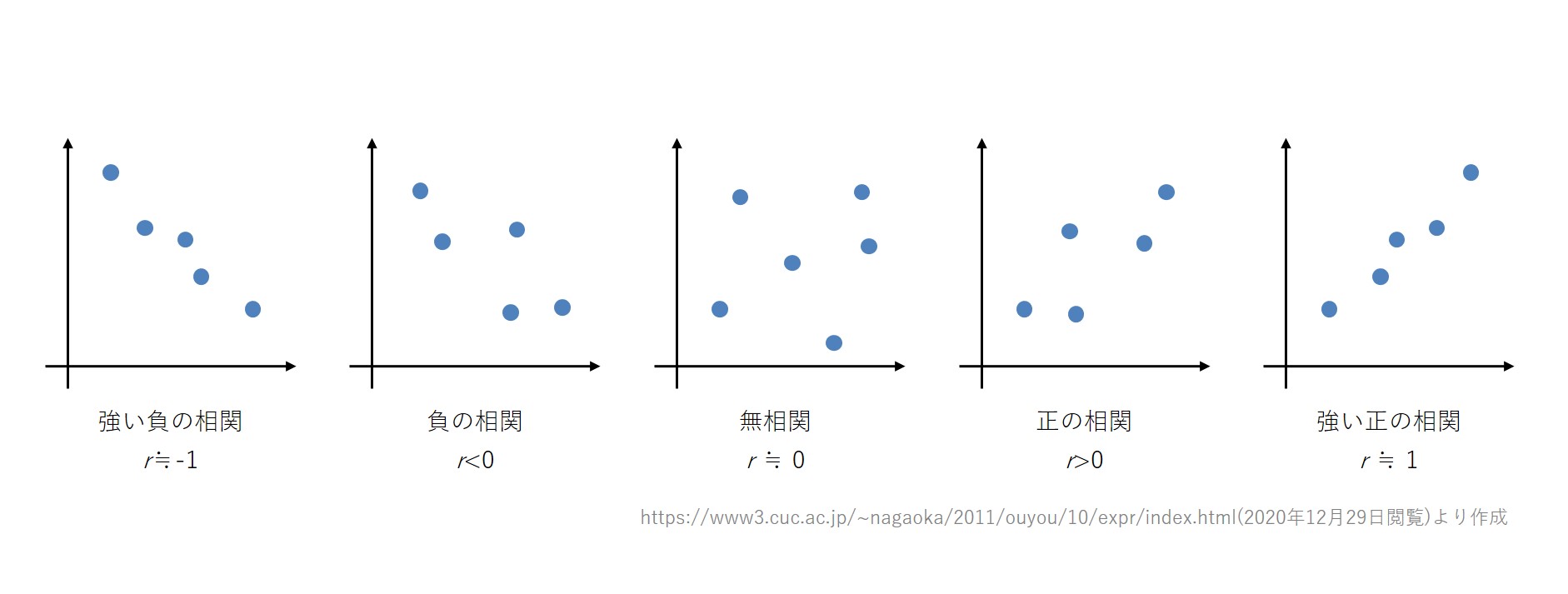
例えば、この図の一番右側のr≒1（ほぼ1という意味です）のグラフを見ると、右肩上がりになっています。先に挙げた(1)と(3)の領域にプロットがかなり多く、直線に近い関係になっているのが分かります。

そこから相関がr＞0（プラスの値）、r≒0と0に近づいていくと、プロットがどんどんばらついていきます。(1)と(3)の領域にプロットが多めに存在してはいますが、それ以外の領域に入るプロットも多くなっています。

このことから、相関係数が1という大きな値から0へと近づいていくと、プロットが(1)と(3)以外の部分に入るものが多くなる、すなわち、2指標の関連がどんどん弱くなっている状態が見てとれます。

r≒0のグラフでは、プロットが(1)、(2)、(3)、(4)すべての領域に広くばらけています。この散布図状況において共分散を計算すると、プラスとマイナスが相殺されてしまうので、それに基づいた相関係数の値も0に近づいていくということです。

逆に、相関係数がr≒0からマイナスの方へ大きくなっていくと、(2)と(4)の領域にプロットが多くなっています。そして、r≒-1のときは、(2)(4)の領域を凝縮した直線のような形にプロットが分布していますね。

このように、相関係数はその大きさでデータの分布状況が把握でき、そこから2指標の関連を捉えることができます。

また、相関係数が極端な値をとる場合(r≒1やr≒-1)では、その散布部におけるプロットはほぼ直線形となり、「一方の指標の値に対して、もう一方の指標の値が完全に対応している」状態になっています。他方、相関係数が0に近い(r≒0)場合では、プロットがばらついており、一方の指標の値に対してもう一方の指標の値の大きさは様々なものになっています。

このことから、相関係数で表される2指標の関係性の強さは、具体的には「一方の指標の値ともう一方の指標の値が、どれだけ正確に対応しているか」であるといえるわけです。

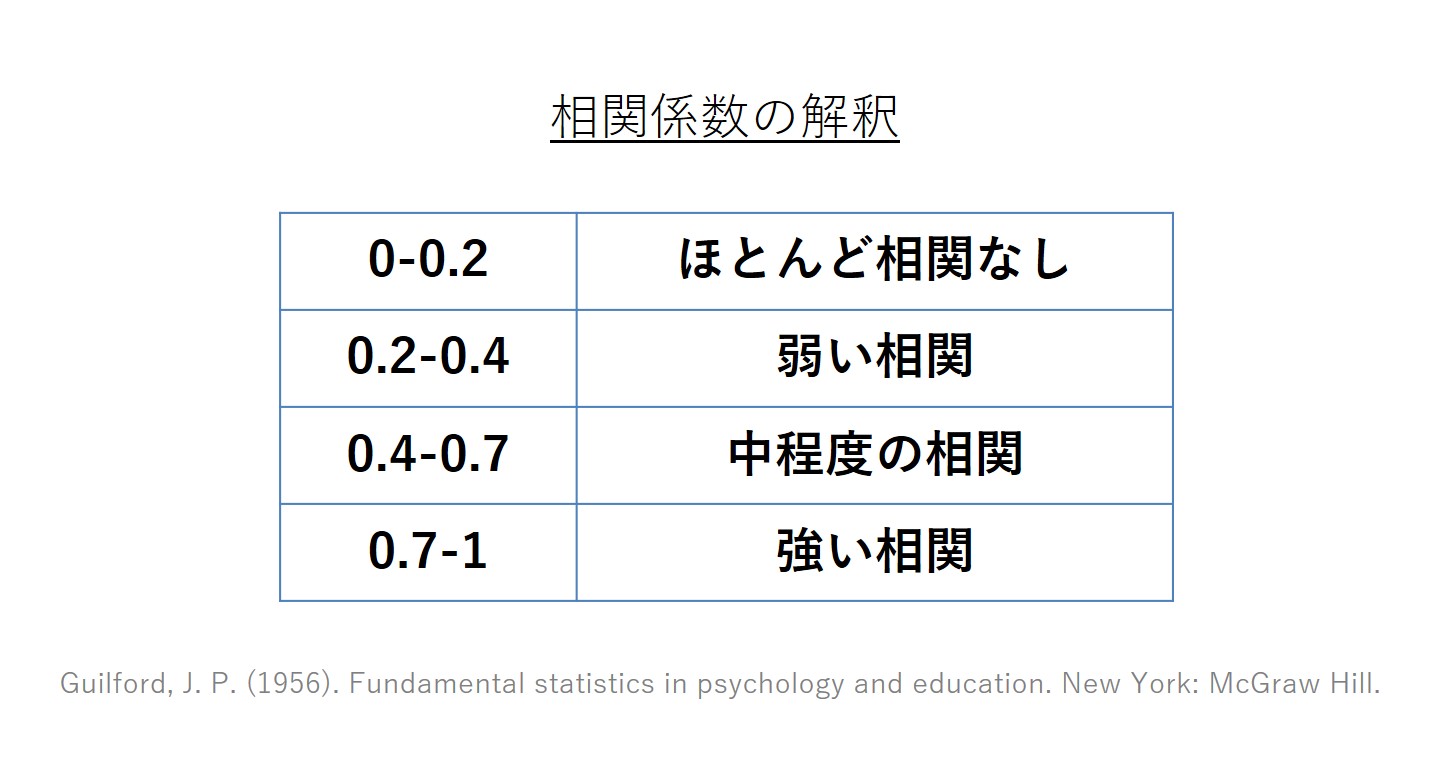
ここで、相関係数が示す関係性の強さの意味は分かりましたが、それがどれぐらいの大きさだったら関係性(相関)が強い/弱いといえるのでしょうか。実は、相関係数の大きさに基づく関係性の強さの解釈は、業界によって違います。相関分析をよく用いる心理学、経営学、社会学の間で違いますし、あるいは経営学の中でも分野によって基準は違います。さらにいえば、その基準を明示せずに相関係数が評価されるケースも多くあります。

ただ、一般に用いられることが多い基準では、相関係数の絶対値（プラス・マイナスを除いた値そのもの）が0.2未満であれば、ほとんど相関がない、0.2を超えてくると弱い相関で、0.4を超えると中程度の相関、0.7を超えると強い相関とみなされています。

相関をめぐる注意点

ここまで、相関の意味するところを説明してきました。しかし相関は、誤解や勘違いされることも多い指標です。ここからは、よくある誤解や勘違いについて整理し、注意点として挙げていきます。

注意点1：傾きは考慮されない

例えば、エンゲージメントと上司サポートの相関が0.48、エンゲージメントと周囲サポートの相関が0.76だったとします。さて、ここで問題です。エンゲージメントを高めるには、上司サポートと周囲サポートのどちらを高めればよいでしょうか。

答えは、「相関からは判断できない」です。なぜ判断できないのかというと、相関係数が表しているのは、あくまで関係の強さだからです。関係の強さだけを表している、ということがポイントです。

上の図のように、相関係数が1だったとしても、その散布図は様々な傾きを持つグラフになります。傾きとは、xとyの関係があったときに、xがyに対して与える影響力のようなものですが、xの増加に対して様々なyの増加のパターン、つまり傾きがあり得るのが分かります。

ただ、全て真っすぐの線になっています。真っすぐの線にプロットが集まっているという状態ではあるけれども、傾きが違う状態である。すなわち、影響力が全く違うということになります。相関係数だけでは、傾きが分からず、影響力の大きさが分からないわけです。

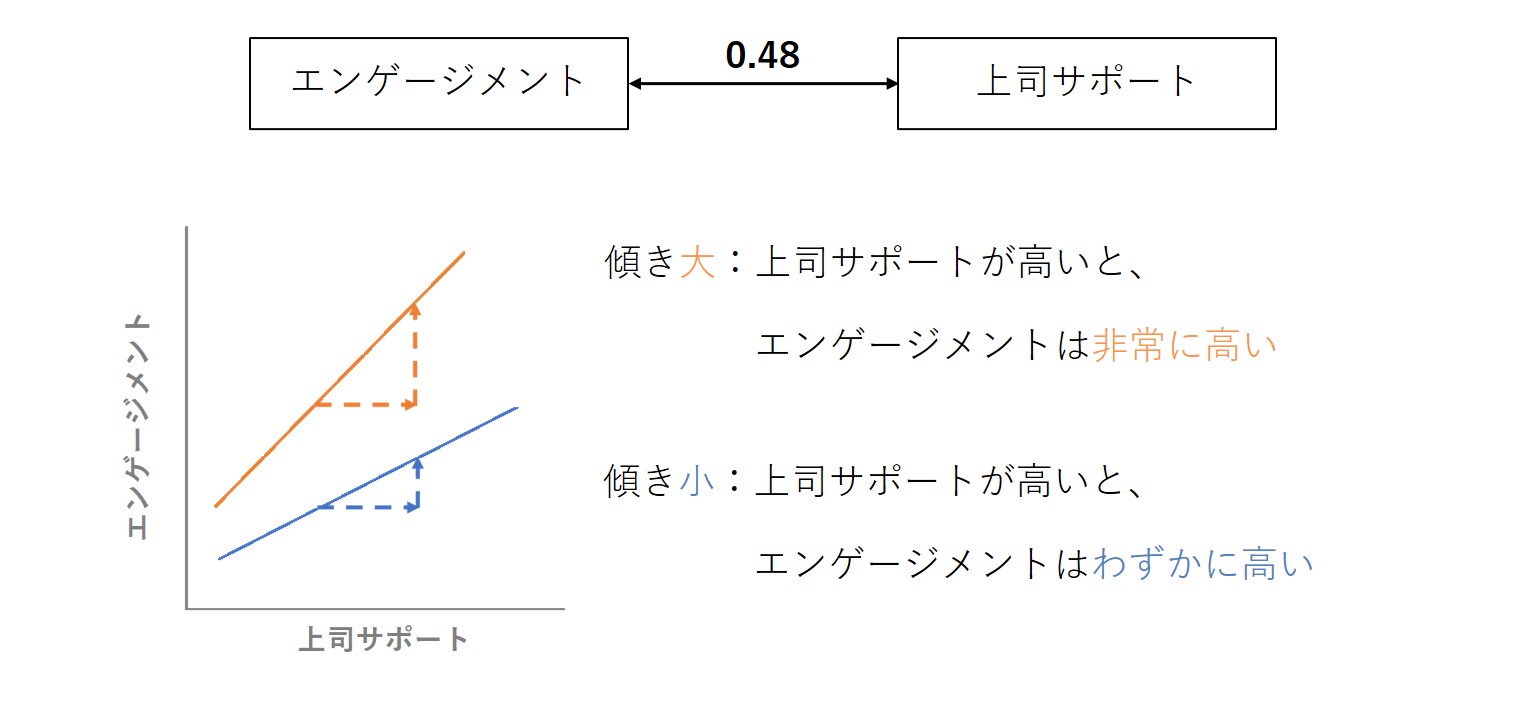
例えば、上司サポートとエンゲージメントを例にして、相関係数は0.48と同じで傾きが異なるような、2つの散布図を考えてみます。傾きが大きいオレンジ色の線の場合、上司サポートを増やすと、エンゲージメントがぐっと高まっています。一方、傾きが小さい青色の線では、上司サポートを増やしても、そんなにエンゲージメント上がらない状態になります。これら2つの散布図は相関係数が同じですが、この例からわかるように、相関係数だけだとこの傾きがわかりません。

分析結果を施策に落とし込んだり、優先順位を付けたりする場合には、傾きも考慮していく必要があります。しかし、相関係数には傾きの情報が含まれていないため、その点には注意が必要です。

ちなみに、ではどうやって傾きを捉えればよいかについては、それは回帰分析という、別の手法があります。そちらについては、別のコラムにて紹介します。

注意点2：本質的に関連がない相関の可能性

2つ目の注意点は、計算された相関が実質的に意味を持たない可能性があることです。

例えば、xとyの間に相関係数が高かったという場合でも、実は、そのxもyも両方とも、zという隠れた変数と指標との間で相関しているだけかもしれない、というケースです。このような相関を疑似相関と呼びます。算出されたxとyの相関というのは疑似的なものだということです。

疑似相関の例としてよく挙げられるのが、プールで溺れる人の人数とアイスクリームの売り上げの相関です。プールでおぼれる人数とアイスクリーム売り上げには、強い正の相関になります。この分析結果から、「アイスクリームが売れると、プールで溺れる人が増える」という解釈ができますが、これはちょっと意味がわかりません。

それではなぜ、これらの間に相関がみられるのでしょうか。それは、第三の変数zにあたる部分として、気温という要因が考えられます。気温が高いとプールに入る人が増えて、その分溺れる人も増えてしまいます。また、気温が高いとアイスクリームの売り上げが上がるという関係性もあります。

このように、プールで溺れる人数とアイスクリームの売り上げがそれぞれ、気温という共通の要因と関連を持っています。その結果として、プールで溺れる人とアイスクリーム売上の間に疑似的な関連が生まれてしまうわけです。こうして、本質的に意味がない相関が見いだされてしまうことがあります。相関を用いる際は、疑似相関の可能性に注意しましょう。

注意点3：相関と因果は異なるもの

3つ目の注意点は、相関は因果関係とは違うという点です。xとyの間に相関関係があるとわかったとしても、それだけではxによってyが高まるということは言えません。「相関と因果は違う」という話です。

因果関係を特定するのは、すごく難しい作業です。古典的に言われていることとして、因果関係を示すための3原則というものがあります。

第1に、2つの指標間に相関が存在していることです。これは、相関係数から把握可能です。

第2に、時間的先行、つまり因果関係において原因xは結果yより先に生じていることです。そのため、因果を証明するためにはいわゆる時系列データが求められます。

第3に他の要因がxとyの関連を生み出す可能性の排除、つまり疑似相関になっていないことです。

近年はさらなる追加要素も提案されていますが、いずれにせよ、因果関係があることへの言及は様々な要素をクリアする必要があります。そのため、相関分析をしただけで因果が証明された、という考え方は誤りだということです。

注意点4：非線形な関連を捉えられない

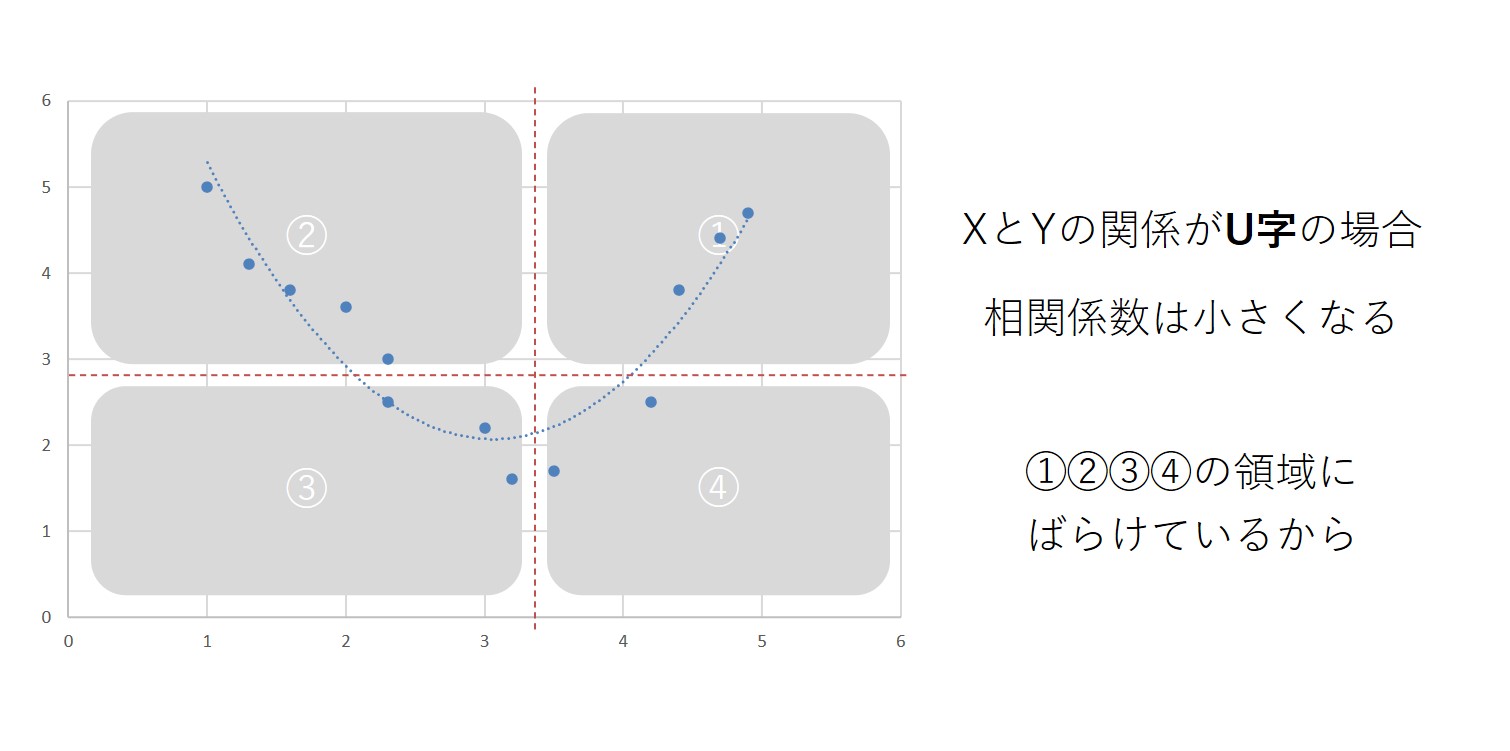
4つ目の注意点は、2指標の関係は直線的でない(非線形)の場合もあるが、相関ではそれが捉えられないことです。

例えば、xとyの関係が散布図を描いたときにu字の関係になっていると、相関係数は小さくなります。u字の関係になってると、(1)から(4)の領域に、プロットが等しくばらけてしまいます。そうなると共分散の値は0に近づいていき、結果、相関係数も小さくなります。

言い方を変えると、相関係数は直線以外の関係を捉えることはできないということです。相関係数は、2つの指標がどれほど直線に近いかということを見る手段に他ならないので、もしかすると、相関係数が小さいとしても、直線的ではない関係性が存在する可能性があります。

そのため、2指標の関連を検証するときは散布図を描くことが大事になります。相関係数だけを算出して終了せず、きちんと散布図を描いて関連の仕方を視覚的に確認するとよいでしょう。

注意点5：外れ値に弱い

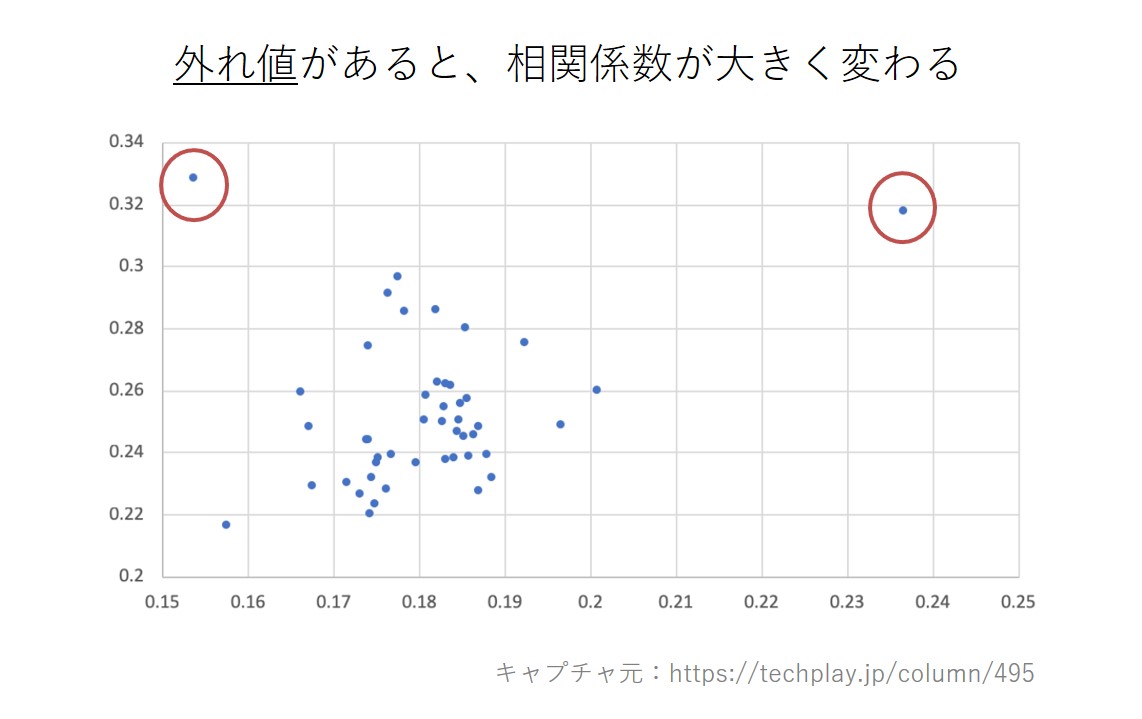
5つ目の注意点は、相関は外れ値に弱いという特徴です。

外れ値とは、上記の散布図のように、全体の傾向から大きく外れているようなプロットのことです。このようなデータがあると、相関係数は著しくその影響を受けてしまい、正確な相関が算出されない恐れがあります。

相関分析を行う際は、相関係数をいきなり見るのではなく、最初に散布図を確認して、外れ値があるかを確認します。外れ値があると相関係数の算出に影響するため、外れ値を取り除くといった作業が必要になります。

注意点6：混合標本に注意

最後の注意点は、様々な集団が混ざった混合標本には注意が必要だという点です。このようなデータの相関を分析する際には、データを分割して、それぞれで相関係数を求める必要があります。

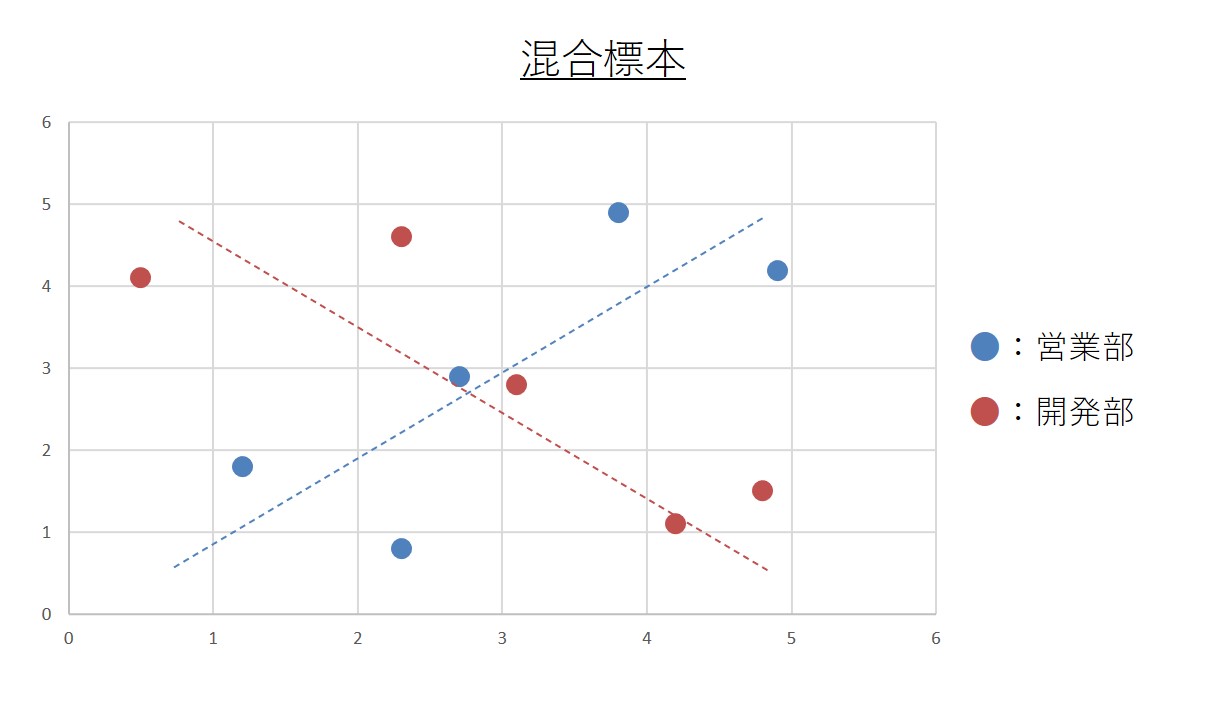例えば、営業部と開発部からデータをとった散布図があります。このデータ全体で相関係数を取ると、相関係数は低くなります。しかし、営業部の青い所だけ見ると正の相関、開発部だけを見ると負の相関があるように見えます。

混合標本は、2つ以上の特徴を持ったデータが混じり込んでいる状態を指します。これが疑われる場合は、データを分けてそれぞれ相関を見ることが必要になります。

以上のように、相関を用いる際には様々な注意点があります。それらに気を付けつつも、相関を使いこなせば、データから有効な情報を見出せるようになれるでしょう。

（了）