2022年5月12日
クラスター分析とは何か
ある企業において、「パフォーマンスの高い人材を探るために、様々な指標を用いて従業員をタイプ分けしたい」と考え、サーベイを実施しました。タイプ分けに用いる様々な指標として、以下のものを測定しました。
- 業務スキルの豊富さ
- 業務知識の量
- 周囲との信頼関係
- 上司からのサポート
- 仕事へのやる気
このような「５つの指標を用いて、従業員をタイプ分けする」ことを考えたとき、読者の皆さんはどのような分析方法を用いますか。仮に２つの指標であれば、各指標の平均を算出して、それを上回る人／下回る人を組み合わせた４タイプを考えることができるでしょう。
例えば、業務スキルの豊富さと周囲との信頼関係の２指標なら、両方が平均より高いタイプ、両方が平均より低いタイプ、業務スキルの豊富さは高いが周囲との信頼関係は低いタイプ、業務スキルの豊富さは低いが周囲との信頼関係は高いタイプといった分け方が考えられます。
しかし５指標ともなると、上記のようなタイプ分けはそう簡単にできません。仮に同じような考え方で５指標を用いたタイプ分けをするとなると、平均の高低の組み合わせパターンは25=32通りとなり、32タイプの違いをそれぞれ考えなければなりません。
このように、３指標以上を用いて回答者をタイプ分けするには、どうすればよいのでしょうか。本コラムでは、回答者のタイプ分けに有効な分析である「クラスター分析」について、解説をしていきます。
クラスター分析とは何か？
クラスター分析とは、分析対象が持つ特徴に基づいてグループ分けすることを目的とした分析です（Hair et al., 2014）。ここでいう分析対象とは、回答者や測定指標など様々なものがありますが、本コラムでは回答者をグループ分けする手法として紹介します。
クラスター分析では、様々な指標に対して回答者たちが報告した回答値や得点を基に、回答者の間に見られる「類似性」を数値化し、それに基づいてグループ分けを行います。
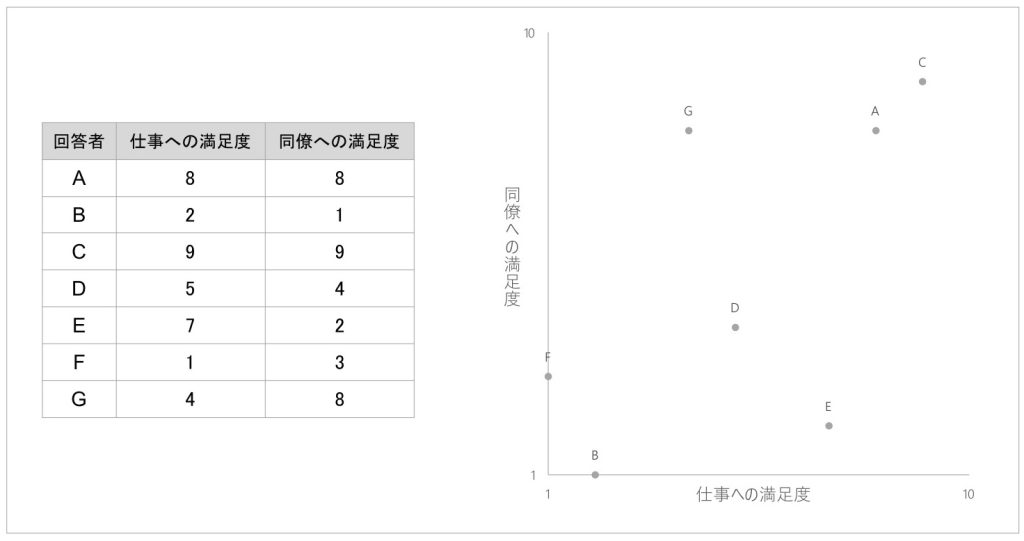
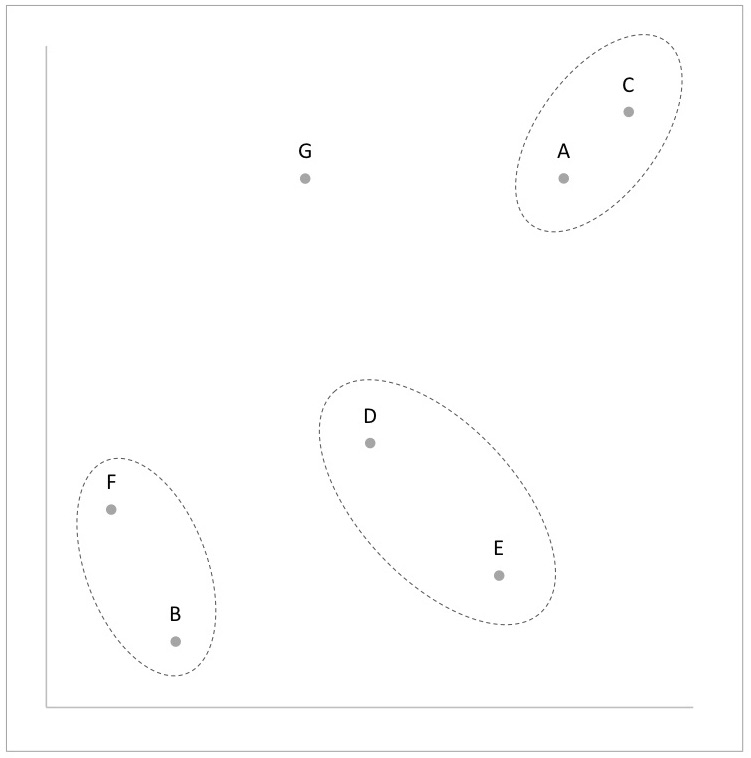
簡単なクラスター分析の例として、７名の回答者から「仕事への満足度」「同僚への満足度」の２指標を1～10点の10段階でそれぞれ報告してもらった架空データを考えてみます。具体的な回答データの内容と、それを散布図としてプロットしたのが図１です。
クラスター分析は、以下の３つの手順を経て行われます。
（１）回答者間の類似度を定義して算出する
クラスター分析では、まず、回答データに基づいて、回答者間の類似度を計算します。回答パターンがどの程度似ているかを類似度として算出するわけですが、どのように計算すればよいのでしょうか。
図２ 回答の類似度と距離の関係
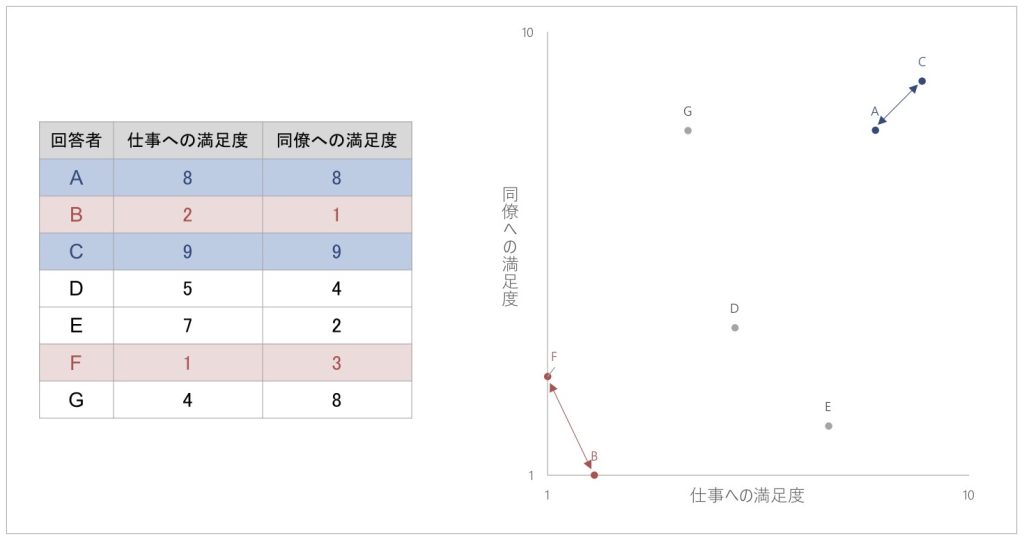
ここで、両方に高得点で回答しているAさんとよく似た回答データのCさんと、両方に低得点で回答している、回答があまり似ていないデータのFさんについて、図２の散布図を見てみましょう。
Aさんと似た回答パターンであるCさんは、Aさんと近い位置にあります。一方、Aさんと似ていない回答パターンであるFさんは、Aさんから遠い位置に存在しています。
同様に、両方低得点で回答しているFさんと似た回答パターンのBさんは、散布図においてFさんと近い位置に存在していることがわかります。BさんはAさん、Cさんと回答パターンが似ていないわけですが、Bさんはその人たちから離れた位置に存在しています。
このようにしてみると、回答データを散布図にプロットしたとき、回答パターンが似たデータは、距離が短い近い位置に配置されることになります。逆に回答パターンが似ていないデータは、距離が離れた遠い位置に配置されることになります。
このことから、データ間がどの程度遠いのかという距離の大きさは、データ同士が互いにどれだけ似ているのかを表す類似度の指標になるとわかります。つまり、回答者の間で類似度を捉えるには、回答データに基づいて回答者間の距離を算出すればよいのです。
以上の考えを用いて、回答者間で距離が短くよく似た回答者をグループ（クラスター）にまとめていくことで、回答者をいくつかのクラスターに分ける分析が、クラスター分析です。
クラスター分析における距離の計算と回答者のクラスタリング方法
クラスター分析に関連して、回答データから距離を算出する計算式は様々なものがあります。ここでは、よく用いられる距離の数式としてユークリッド距離を解説します[1]。
図３ ユークリッド距離の計算式
ユークリッド距離は、中学数学で学んだ２点間の距離の公式や、高校数学で学んだベクトルの長さの公式そのものです。２名の回答データについて、各指標の各次元への回答値で差を算出し、それらを２乗して足し合わせたものの平方根を取ります。直感的に理解しやすい距離の計算式でしょう。
先の例で挙げた回答者間の距離をユークリッド距離にて算出し、距離行列としてまとめたのが図４になります[2]。
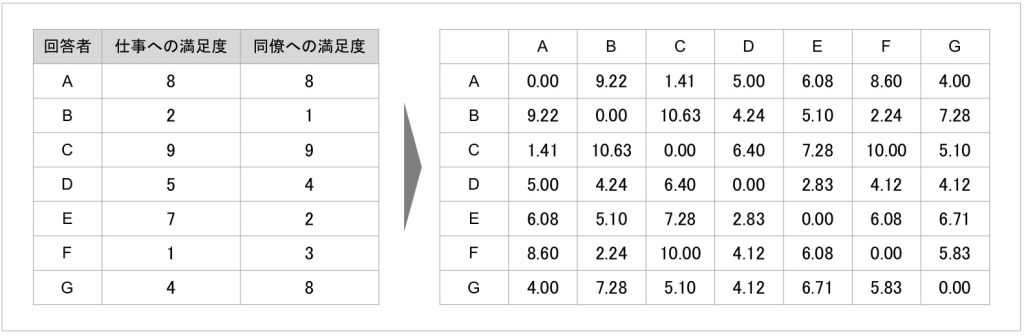図４ ２指標の回答データから作成した７名の回答者における距離行列
これによって、回答者が互いにどれだけ離れているかの距離が算出され、まとめられました。この距離情報は、回答者の回答パターンが類似している程度であったことを踏まえると、図３の左表で示された値は「数値が小さい＝距離が短いほど、回答者同士がよく類似している」ことを表すと判断できます。
この性質を利用して、クラスター分析では回答者のグループ作成を進めていくのです。
（２）回答者間の距離が近い順にクラスターを集約していく
回答者間の類似度を距離行列として整理できたら、次に、距離情報を用いて回答者のグルーピングを行っていきます。クラスター分析によって回答者をクラスターに集約していくことを「クラスタリング」と呼びます。
クラスター分析における回答者のクラスタリングの発想は非常に単純です。それは「よく似た回答者同士＝距離が近い回答者同士を、同じクラスターのメンバーと見なしてまとめる」、これを繰り返すだけです[3]。
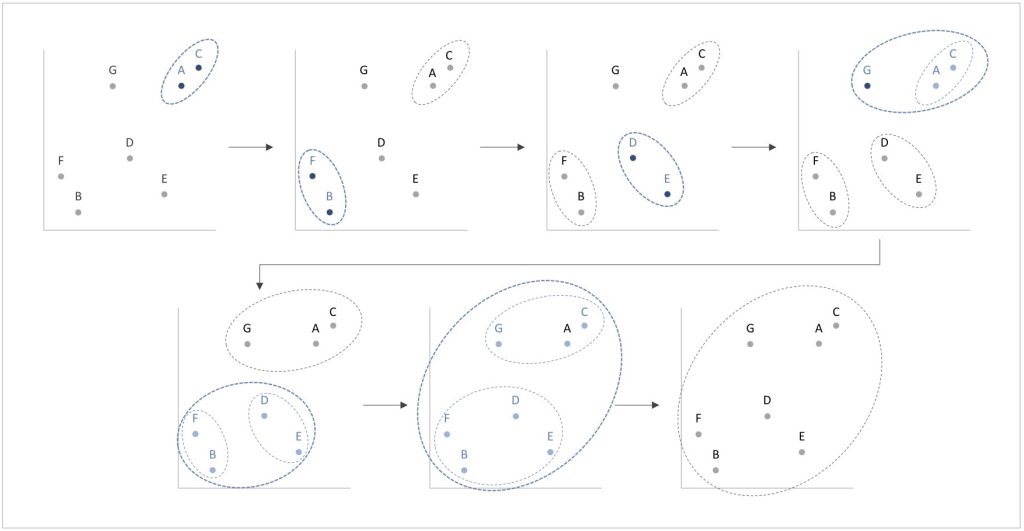
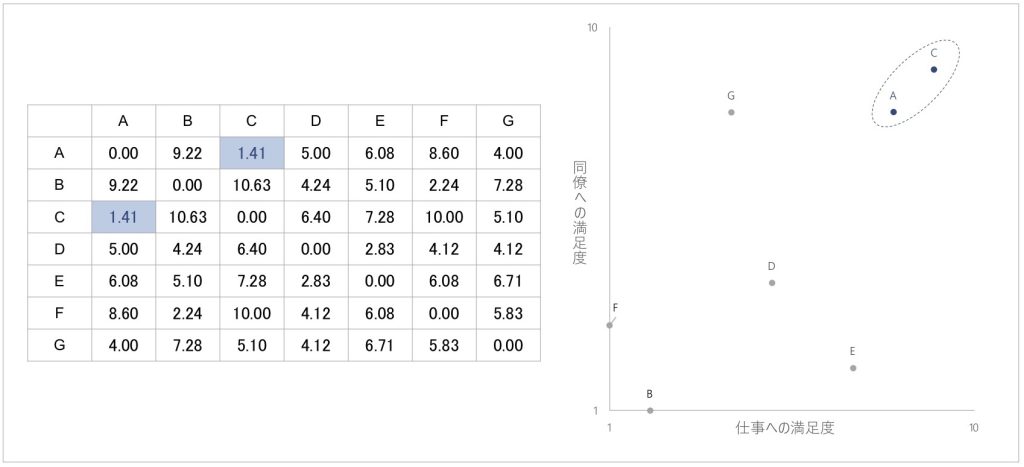図５ ７名の回答者における距離行列を用いたクラスタリングの展開
先ほど作成した距離行列を例に考えてみます。７名の回答者で作成した上記の距離行列において、もっとも距離が近い、つまりよく似ている回答者は、AさんとCさんです。そこで、まずはAさんとCさんをクラスタリングします。
ここで、２名がクラスタリングされて一つにまとまったことで、クラスターと他の回答者との距離を再計算する必要があります。本コラムでは、研究で用いられることも多いウォード法（Ward method：Ward, 1963）について紹介します[4]。
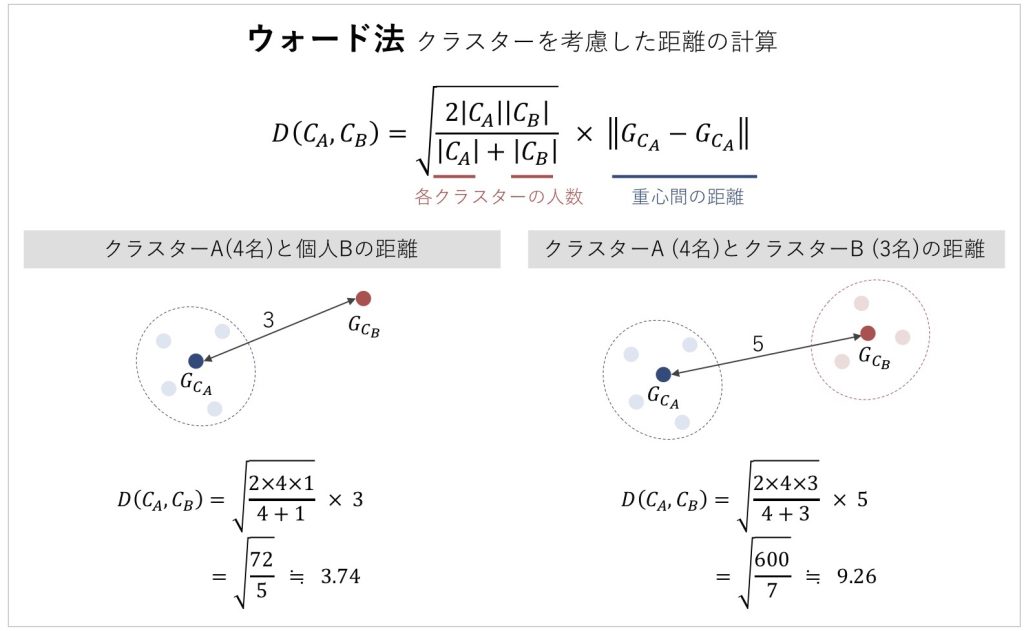
図６ ウォード法による距離の計算
ウォード法では、各クラスター内の回答データのばらつき（分散）を最小化することを目指し、各回答データの重心に着目して距離を算出する方法になります。この方法では、各クラスターにおける重心点を計算し、各クラスターの人数によって重心間の距離の大きさを調整することで、クラスターと回答者の距離が求められるのです[5]。
図６にあるように、ある回答者（個人）とクラスター間の距離を計算する際は、その回答者における重心は回答者自身になります。そのため、重心間の距離はクラスターの重心とその回答者の距離をとります。このようにして、作成されたクラスター（CL1：Cluster 1）と各回答者との距離を再計算します。
図７ クラスタリング後に再計算した距離行列
以降も同じ手続きを繰り返し、距離行列から距離が近い回答者やクラスターを探してクラスタリングしては、距離行列の再計算を繰り返していきます。図７の距離行列でいえば、次にクラスタリングされるのはBさんとFさんになります。
このプロセスをある程度進めると、複数のクラスターが形成されていくのですが、そこでクラスタリングは終わりません。図６にあるように、距離の再計算はクラスター同士でも行われ、距離が近いクラスター同士がさらにひとつにクラスタリングされていきます。
２つのクラスター間の距離をウォード法により計算するには、それぞれのクラスターにおける重心を算出し、図５の数式に当てはめて距離を計算していきます。これを最後まで繰り返していくと、最終的にすべてのクラスターがひとつのクラスターに集約され、クラスタリング計算は終了となります。
図８ クラスターが集約されていくプロセス
（３）回答者をいくつのクラスターに分割するか決定する
クラスタリング計算を最後まで繰り返したら、その集約過程を可視化して、回答者をいくつのクラスターに分割すればよいか判断します。
図９ クラスター分析で出力されるデンドログラム
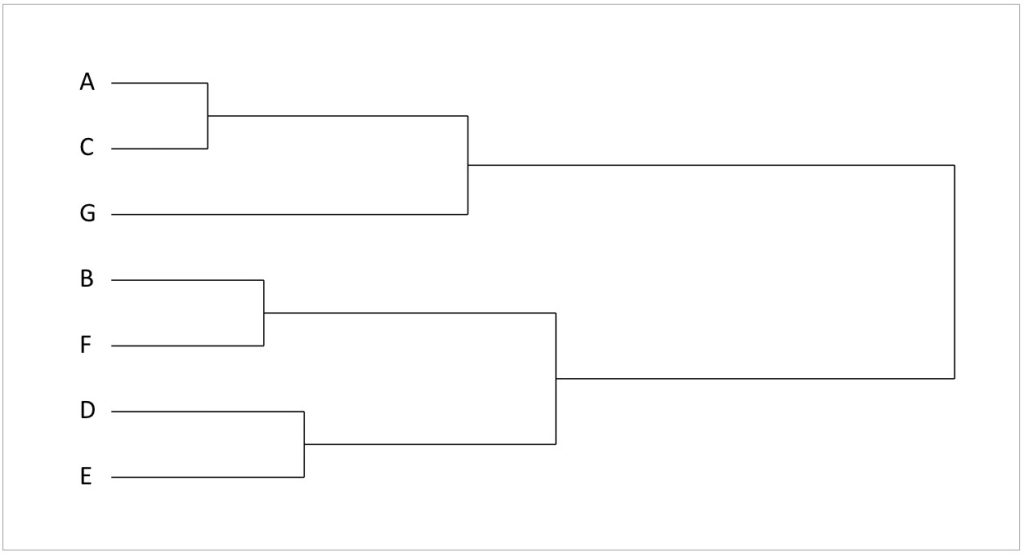
クラスターの集約過程を可視化したグラフを「デンドログラム」と呼びます。デンドログラムは、横軸に距離のデータを取り、回答者やクラスターがそれぞれどの程度の距離で集約されたのか、そのプロセスが図示されています。
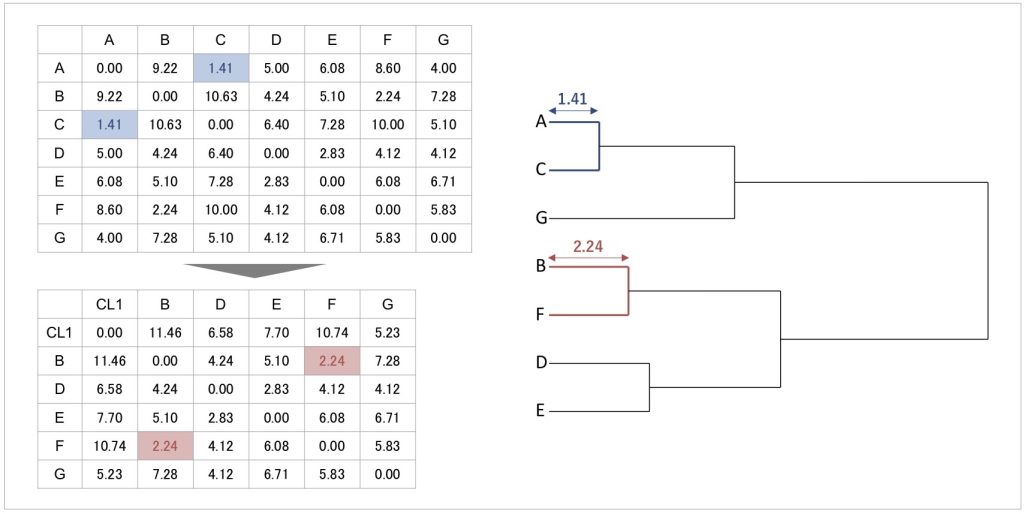
図10 デンドログラムの見方
デンドログラムの見方を距離行列と照らし合わせてみてみましょう。例えば、左上の最初の距離行列を見ると、AさんとCさんの距離が1.41と最も短く近い位置にあり、最初にクラスタリングされていました。これに対応して、デンドログラムのAさんとCさんがまとまる地点で、横軸が表す距離の長さは1.41となります。
AさんとCさんがクラスタリングされた後に、クラスターと回答者間の距離が再計算され、距離行列が更新されます。それを見るとBさんとFさんの距離が2.24で最短です。そのため、デンドログラムでもBさんとFさんがひとつにまとまっており、BさんとFさんがまとまる時点において横軸で表される距離は2.24です。
このようにデンドログラムは、どの回答者同士がどの順でクラスタリングされるか、そしてクラスタリングがどの程度の距離の時点で行われたかを可視化したものになっています。
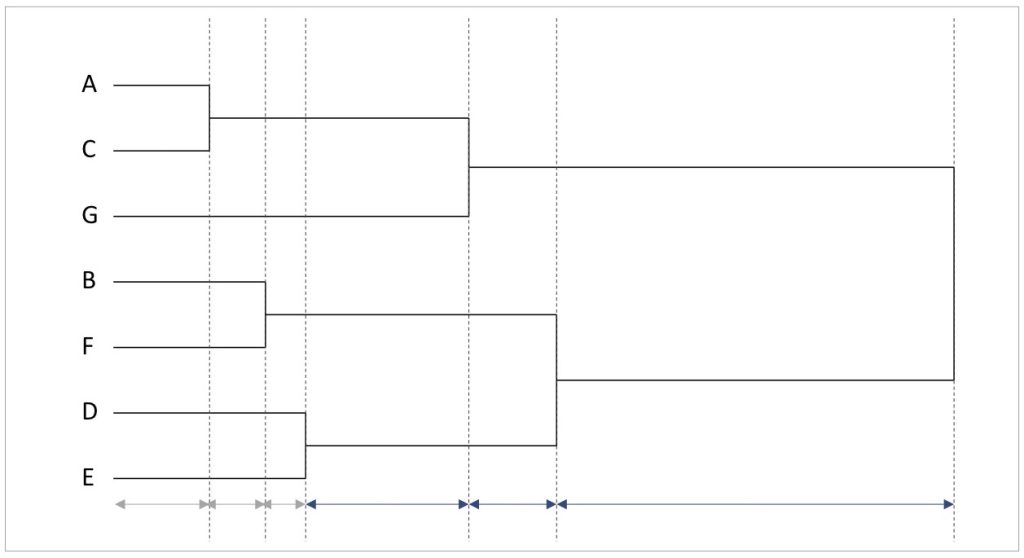
クラスター分析では、デンドログラムを用いて回答者をいくつのクラスターに分割するか決めていきます。判断の決め手は「デンドログラムにおいて、次のクラスタリングまでの距離が長くなり始めたポイントに着目する」ことです。
図11 デンドログラムからクラスター数を決定する
デンドログラムにおける横軸は、各クラスタリングが行われる距離を表していました。ここで、クラスター分析では、距離が短いほど回答者同士が類似していることを踏まえると、「クラスタリングされるまでの距離が長い＝クラスター同士が似ていない」と解釈できます。
したがって、デンドログラムにおいて、次のクラスタリングまでの距離が長くなり始めた箇所は「類似していない異質なクラスター同士を集約し始めた部分」に該当します。
似ていない者同士を同じクラスターに集約するのは、似た者同士をタイプ分けするという分析目的に反します。そのため、そこでクラスタリングを停止し、その時点におけるクラスター分割を採用するのが妥当だと判断できるのです。
この発想に基づくと、図11のデンドログラムにおいて、次のクラスタリングまでの距離が長くなり始めたのは左から４つめの青矢印の地点です。ここでは、Aさん、Cさんのまとまり、Gさん個人、BさんとFさんのまとまり、DさんとEさんのまとまりの４クラスターが現れています。
そこから、Aさん・CさんとGさんが合流するのですが、ここでクラスタリングまでの距離が長くなっています。つまり、異質な者同士が集約され始めたタイミングはこのあたりだとわかります。実際に、そのタイミングの散布図を見ると、その時点では類似したデータ同士がクラスタリングされていることがわかります。
図12 ４クラスター時点での散布図とクラスタリング状況
このデンドログラムからは、４クラスター以降の選択肢、つまり２～４クラスターのうちどこかでクラスタリングを終了するのが妥当と判断できます。
なお、このような方法でクラスターをいくつにするか考えたとしても、結局は主観的な判断です。あるいは、いくつのクラスターに分割するか判断が難しく感じることもよくあります。そのときは、後ほど解説する「クラスターごとの特徴把握」にて、様々なクラスターの特徴の違いを解釈し、よりよいクラスターの数を考えます。
実際のクラスター分析の展開
以上が、クラスター分析を用いた回答者のグループ分けになります。ここからは、５指標を測定した最初の例をもとに、200名を対象としたデータを取得した架空データを想定します。そして、そのデータにクラスター分析を適用した展開を追っていきます。
１．必要に応じた各指標の「標準化」処理
最初に、クラスター分析に用いる指標について、気を付けるべきポイントがあります。それは、「ユークリッド距離を用いてクラスター分析する場合、分析に投入する各指標の得点範囲や測定件法が違っているならば、全ての得点を標準化する必要がある（Hair et al., 2014）」ということです。
標準化とは、ある指標の得点範囲を平均0, 標準偏差1にする計算処理のことです[6]。各指標の得点範囲が違うときに標準化が必要となる理由は、得点範囲が大きい指標によって距離の大きさが左右され、範囲が小さい指標の特徴はほとんど反映されなくなるからです。
図12 得点範囲が異なる指標を投入してそのまま距離を計算した場合の問題
この問題について、例として図12を見てみましょう。ここでは、0～100点で評価した業務スキルテスト得点と１～５点の範囲で評価した仕事満足感を用いて、AさんとBさんの回答データ間のユークリッド距離を算出しています。
２名の得点を見ると、Aさんの方がBさんよりも業務スキルはやや高い程度ですが、その一方で、仕事への満足度はBさんよりも著しく低いことがわかります。しかし、この２名で算出された距離の情報は、仕事への満足度に見られる問題が軽視される結果になっています。
仮に、業務スキルテスト得点のみでAさんとBさんの距離を計算すると、15になります。一方、１～５の得点範囲の仕事への満足度において、AさんとBさんでは得点に大きな違いがあるのに、図12の距離計算においては、実質的に0.30点分しか貢献していないのです。
これは、仕事満足感の得点範囲に対して業務スキルテストの得点範囲は非常に大きいため、二人の間にあるユークリッド距離のほとんどは業務スキルテストの得点によって左右されていることが原因です。それに飲まれる形で、得点範囲の小さい仕事への満足度は、算出された距離の値に対してほとんど意味をなさなくなるのです。
そのように算出した距離データでクラスター分析をすれば、当然、クラスタリングも業務スキルテストの情報でほとんど決まってしまいます。分析上は２指標を入れたタイプ分けを狙ったのに、実質的に１指標によるタイプ分けをしている状態です。仕事への満足感が非常に低い問題も見過ごされてしまうでしょう。
上記は極端な例ですが、例えば１～４点の範囲で回答を求めた指標と、１～７点の範囲で回答を求めた指標を分析に投入しても、同じ問題は生じます。「各指標の得点範囲」というデータ分析の目的と本質的に関係がない特徴によって、距離計算に想定外の偏りが生じる問題が、クラスター分析に潜んでいるのです。
そういった問題を避けるため、得点範囲が異なる指標を用いる場合や指標間の得点のばらつき（標準偏差）に大きな違いがある場合は、分析に投入する全ての指標の得点を事前に標準化するのが良いといえます。
今回の分析に用いる５指標「業務スキルの豊富さ」「業務知識の量」「周囲との信頼関係」「上司からのサポート」「仕事へのやる気」のうち、業務スキルの豊富さと業務知識の量は７件法、残る３つは５件法で測定したデータです。
このデータは指標間で回答範囲が異なる問題があるため、分析前に各指標において標準化の処理を行っています。このように、クラスター分析をする前に各指標の得点範囲を確認することが重要です。
２．デンドログラムの出力とクラスター数の決定
標準化の処理を行ったら、クラスター分析のために回答データから200名の回答者間の距離行列を作成し、クラスター分析を行います。距離行列やクラスタリングの計算を経て、出力されたデンドログラムが図13です。
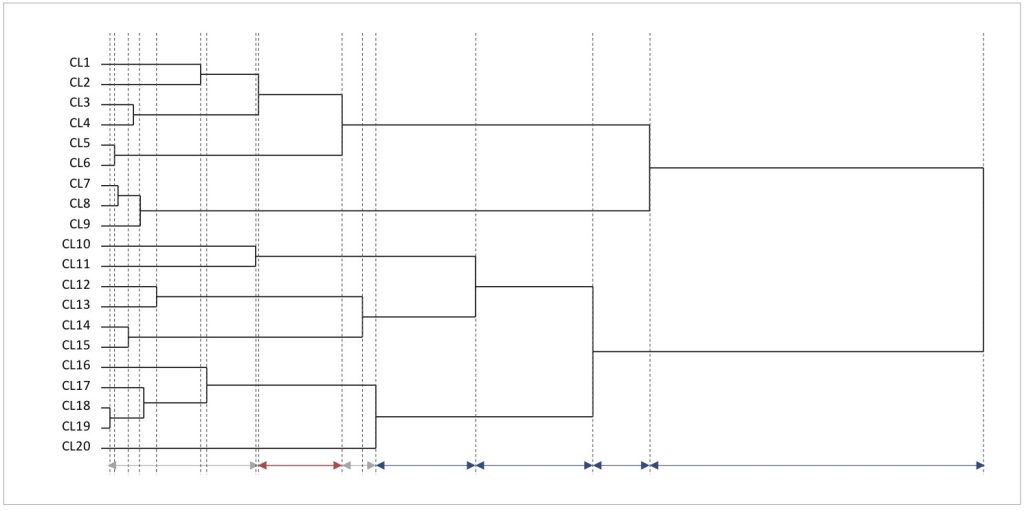図13 200名5指標の回答データから得られたデンドログラム
100名を超える規模の実際の調査では、回答者レベルで少しずつ集約される過程が非常に膨大になります。そのため、多くの分析ツールでは個々の回答者から出力を始めず、いくらか集約されたクラスター（CL）から始まる形でデンドログラムが出力されます。
デンドログラムを見ると、今回のデータでは、８クラスターに集約される赤矢印の箇所がいくらか長くなっており、その後、５クラスターに集約される青矢印の箇所から、また長い横線になっています。
このことから、８クラスターから７クラスターにクラスタリングされる時点でいくらか異質なクラスターがまとまり、さらに５クラスター以降のクラスタリングによって、より異質なクラスターがどんどん集約されていったと考えられます。
ここで、今回の分析目的はタイプ分けであり、ある程度の個数のクラスターに分割したいと考えている設定でした。８クラスターはややタイプが多く、意味づけが難しいと考えられることから、４クラスターと５クラスターのどちらかを採用する狙いで、それらの結果を取り上げることにしてみましょう。
クラスターごとの特徴を把握する
ここからは、クラスター分析の結果得られた各クラスターの特徴を把握し、どのような回答パターンの回答者に分かれたのか検証をしていきます。ここで様々なクラスター数における分かれ方も確認し、最終的にどのクラスター数を採用するか決定していきます。
各クラスターの特徴検証では、分析に投入した指標の平均得点をクラスターごとに算出し、得点の状態を比較する手法がよく用いられます。つまり、単純に「分析に用いた指標についてクラスターごとに比較し、特徴を考える」ことになります。
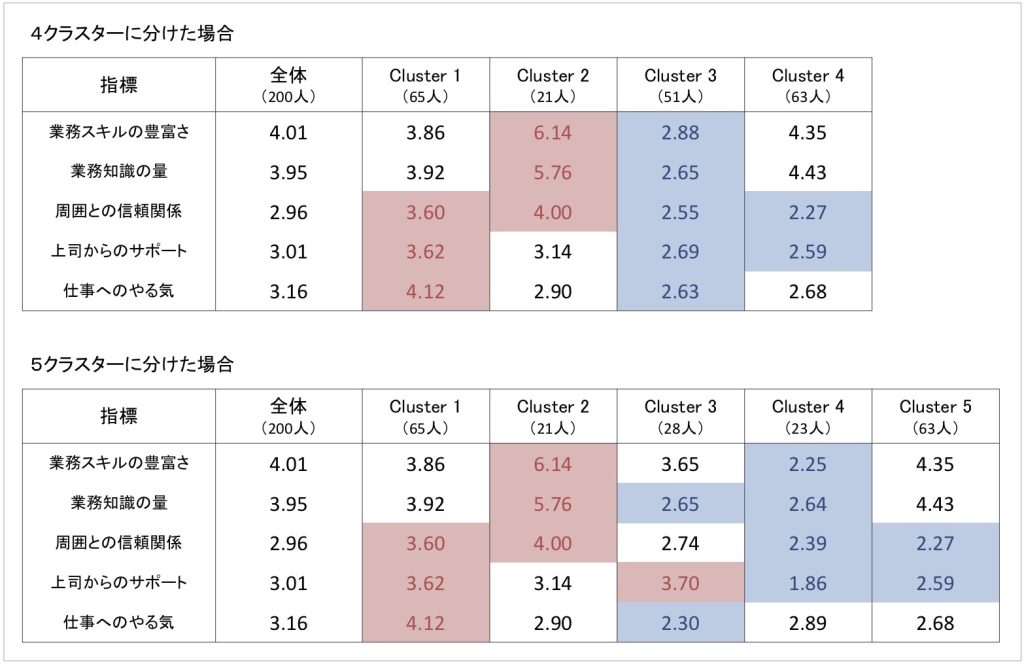
先ほどのクラスター分析において、４クラスターで分けた場合と５クラスターで分けた場合のそれぞれで、各クラスターの５指標それぞれの平均得点を算出したものが図14です。
図14 ４クラスター・５クラスターそれぞれの場合の５指標の平均得点
各クラスターの特徴把握は、各指標の全体平均と各クラスターの得点を比較したり、クラスター間で得点を見比べたりするなどして、総合的に判断します。ここでは、暫定的に全体平均より0.5点以上のところを赤く、0.5点以下のところを青く塗り、各クラスターの特徴をわかりやすく示しています[7]。
まず、４クラスターの結果を見て、各クラスターの特徴を見てみましょう。Cluster 1は業務スキルの豊富さや業務知識の量などの能力面は平均的ながら、周囲との信頼関係や上司からのサポートは平均より高く、仕事へのやる気も高いクラスターです。このことから、Cluster 1は「対人関係基盤のハイモチベーションタイプ」と考えられます。
Cluster 2は業務スキルの豊富さや業務知識の量など能力面が平均や他のクラスターよりも非常に高く、同時に、周囲との信頼関係も平均より高くなっています。他方、上司からのサポートや仕事へのやる気は平均的です。このことから、Cluster 2は「ハイパフォーマータイプ」と呼べるでしょう。
Cluster 3は、業務スキルの豊富さや業務知識の量など能力面、周囲との信頼関係や上司からのサポートなどの対人面、そしてやる気も合わせて、すべてが平均を下回っていることが大きな特徴です。このことから、Cluster 3は「ローパフォーマンス・要注意タイプ」と考えられます。
最後にCluster 4は、業務スキルの豊富さや業務知識の量といった能力面と仕事へのやる気が平均的であり、仕事面は問題なさそうです。他方、周囲との信頼関係や上司からのサポートといった対人関係が平均より低いことが特徴です。このことから、Cluster 4は「対人関係不安群」とラベリングできるでしょう。
次に、５クラスターに分けた場合を見てみましょう。ここでよく見ると、５クラスターにおけるCluter 1, Clutser 2, Cluster 5は、４クラスターに分けた場合のCluter 1, Clutser 2, Cluster 4と全く同じものになっています。違っているのは、5クラスターのCluster 3, 4と４クラスターのCluster 3だけです。
さらに見ると、４クラスターのCluster 3の人数と、5クラスターのCluster 3, 4の人数の合計は同じになっています。このことから、「５クラスターのCluster 3, 4が、クラスター分析の過程でひとつにクラスタリングされて、４クラスターのCluster 3が生まれた」とわかります。
クラスター分析は、近いもの同士をクラスタリングしてまとめていくという動きが、ここからも見えてくるでしょう。いずれにせよ、４クラスターと５クラスターで３つのクラスターの内容は一緒であるため、５クラスターの場合で確認すべきはCluster 3とCluster 4の特徴になります。
５クラスターの場合のCluster 3は、上司からのサポートは平均以上ながら、業務知識量と仕事へのやる気が平均より低く、業務スキルの豊富さと周囲との信頼関係は平均並みといった状態です。このことから、「サポート空振り・要注意タイプ」と考えられます。
５クラスターの場合のCluster 4は、やる気は平均並みながら他の指標は全て平均を下回り、業務スキルの豊富さや業務知識の量、上司サポートが非常に低いことが大きな特徴です。このことから、「放置気味ローパフォーマー・要注意タイプ」といえるでしょう。
クラスターの特徴把握によって、従業員の様々なタイプを見出すことができました。最後に、４クラスターの結果と５クラスターの結果のどちらを採用するかは、分析者の判断によります。
判断のポイントは、２つの結果の違いを分析目的と照らし合わせて考えることです。先ほど述べた通り、今回得られた２つの結果の違いは「４クラスターの場合でCluster 3と一つにまとまっていたクラスターが、５クラスターの場合で分割されてCluster 3, 4になった」点でした。
この違いを細かく見ると、４クラスターにおけるCluster 3は、他のクラスターと比べてとにかく全般的に得点が低いことが強調されるタイプでした。他方、５クラスターにおけるCluster 3, 4は、その得点の低さのタイプをさらに細分化したような結果が示されています。
すなわち、ここで分析者が判断することは、今回のタイプ分けにおいて「得点の低い要注意従業員のタイプを細分化する必要があるか否か」です。最初に述べたこのサーベイの目的は、パフォーマンスの高い従業員の特徴を探ることでした。
すると、パフォーマンスが低い人の特徴にはあまり関心がないため、それに向けた要注意従業員の細分化は、敢えて無視する方針も考えられ、その場合は４クラスターの結果を採用するでしょう。あるいは、パフォーマンスの低さまで目を向けて、要注意従業員の細かいタイプ分けも考慮し、５クラスターを採用するのも一考です。
仮に「多くの人数が割り振られる、大まかなタイプ分けで捉えたい」という別の目的があるならば、低得点の細かなタイプ分けに目をつぶり、クラスター分割を抑えた４カテゴリーを採用することも考えられます。
このように様々な決定方針がありえますが、いずれにせよ、いくつのクラスターの結果を採用するかは、分析者の判断にゆだねられるのです。得られた結果の違いをよく観察しつつ、タイプ分けしようとした分析目的を意識しながら、最終的なクラスター、すなわちタイプ分けの種類を決めていきましょう。
クラスター分析の注意点
クラスター分析を用いることで、回答者の様々なタイプ分けが可能となります。しかしながら、クラスター分析には様々な注意すべきポイントがあります。
１．適当にデータを入れても、何らかのクラスタリング結果を出力できてしまう
クラスター分析は、計算内容が簡便な分析です。そのため、適当にとったデータでも、クラスター分析を実施してしまえば、何かしらの結果が出力できてしまいます。しかし、当然ながら、何の考えもなしに測定したデータで分析した結果は何の意味も持ちえません。
クラスター分析で計算される距離の情報は、分析に含める指標の出し入れで大きく変わり、出力される結果も全く違うものになります。分析に含める指標の取捨選択は、クラスター分析の結果を大きく左右する大切なポイントです。
「回答者のタイプ分けに、その指標は本当に必要なのか」「分析後の特徴比較で、クラスター間に得点差がないような無意味な指標はないか」など、分析に投入した指標がタイプ分けに有効に機能しているかは、常に意識して考えるべきです。
２．得られた結果はそのデータにおける暫定的な結果である
クラスター分析は、いわゆる推測統計学的な母集団を想定した結果の一般化プロセスを含んでいません[8]。そのため、分析結果が調査に回答していない人たち全般にあてはめて議論することは困難です。
あくまで、その調査に回答者において暫定的に見出だされたタイプ分けであることは、頭の中にとどめておく必要があります[9]。
３．外れ値に左右されやすい
クラスター分析は、外れ値に敏感に反応して結果が変わってしまう特徴もあります。外れ値となる回答者がいた場合、その回答者を含むクラスターもいびつなものになります。そして、そのクラスターを基に距離が再計算されてクラスタリングが続くため、その歪みの悪影響は最後まで残り続けるのです。
極端な回答データが、回答として考えうる範疇のものであれば、それは回答者の実態を表すものであり問題はありません。他方、すべて高得点を付け続けるなど、適当な回答によるものだと予測できるような外れ値の回答は、事前に確認して除外するよう努めましょう。
本コラムでは、複数の指標を用いたタイプ分け・グループ分けに有効なクラスター分析について解説しました。様々な指標を考慮したタイプ分けに関心のある方にお勧めの分析手法です。
引用文献
Hair, J. F., Black, W. C., Babin, B. J., & Anderson, R. E. (2014). Cluster Analysis. In J. F. Hair, R. E. Anderson, R. L. Tatham, & W. C. Black (Eds.) Multivariate data analysis. Upper Saddle River, NJ: Prentice Hall.
Kaufman, L., and Rousseeuw, P. J. (2005). Finding Groups in Data: An introduction
to cluster analysis. New York, NY: John Wiley & Sons, Inc
Ward, J. H., Jr. (1963). Hierarchical Grouping to Optimize an Objective Function. Journal of the American Statistical Association, 58, 236–244.
脚注
[1] 他に、データ間の相関を考慮したマハラノビス距離や、ユークリッド距離のように２点間の最短直線距離でなく、縦・横と直角に移動した場合の距離を扱うマンハッタン距離など様々なものがあります。
[2] 距離行列の見方や距離情報の詳しい解説は、当社コラム「多次元尺度法の基本的な考え方」を参照してください。
[3] 本コラムで紹介するクラスター分析は、階層クラスター分析であり、非階層クラスター分析は扱っていません。階層と非階層の使い分けは、主にサンプルサイズで判断され、階層クラスター分析は400名以下の場合、非階層クラスターは1000名以上の場合に特に利用が推奨されます（Hair et al., 2014）。組織サーベイにおいて1000名以上のデータを取得する場合は多くないでしょう。そのため、本コラムでは階層クラスター分析を解説しています。
[4] この他に、最短距離法、最長距離法、群平均法など様々な計算手法が存在します。その中でも、特にウォード法は最終的なクラスターにおおよそ同じ程度の人数が含まれるようクラスタリングがされるという特長があり（Hair et al., 2014）、研究で用いられることが多い手法です。
[5] ウォード法の元々の計算式は各クラスター内の分散に着目しており、距離情報そのものでなく距離の二乗値（ユークリッド平方距離）を扱います。そのため、元の数式では距離情報を直接計算できません。それに対して、ウォード法の数式は単純な距離の式に変換する手法が提案されており（Kaufman & Rousseeuw, 2005）、本コラムではそちらを紹介しています。
[6] 標準化については、当社コラム「人事のためのデータ分析入門：『回帰分析～要因を見出すための分析～』（セミナーレポート）」で解説していますので、適宜ご参照ください。
[7]各クラスターの特徴をより厳密に検証するならば、分散分析により各群の得点差が有意か否かを検証するなど含めたほうが適切です。
[8] この議論の詳しい解説は、当社コラム「人事のためのデータ分析入門：『統計的に有意』とは何か（セミナーレポート）」をご覧ください。
[9] この問題に対処し、「調査に回答していない人も含めてより広く適用できる、サーベイ対象者のタイプ分けを検証したい」と考える場合、潜在プロフィール分析と呼ばれる分析があります。
執筆者
能渡 真澄
信州大学人文学部卒業，信州大学大学院人文科学研究科修士課程修了。修士（文学）。価値観の多様化が進む現代における個人のアイデンティティや自己意識の在り方を，他者との相互作用や対人関係の変容から明らかにする理論研究や実証研究を行っている。高いデータ解析技術を有しており，通常では捉えることが困難な，様々なデータの背後にある特徴や関係性を分析・可視化し，その実態を把握する支援を行っている。
