2025年7月15日
サーベイの回答者、その人数で大丈夫?サンプルサイズの理論と実践(セミナーレポート)
株式会社ビジネスリサーチラボは、2025年6月にセミナー「『サーベイの回答者、その人数で大丈夫?』:サンプルサイズの理論と実践」を開催しました。
組織サーベイを実施する際、「一体、何人から回答を集めれば十分なのだろうか?」という問いは、多くの担当者が抱える悩みです。 本セミナーでは、この「サンプルサイズ(回答者数)」をテーマに、統計学的な背景を紐解きながら、実際のサーベイ設計や分析に役立つ実践的な知見をご紹介しました。
※本レポートはセミナーの内容を基に編集・再構成したものです。
サンプルサイズが生む問題
能渡:
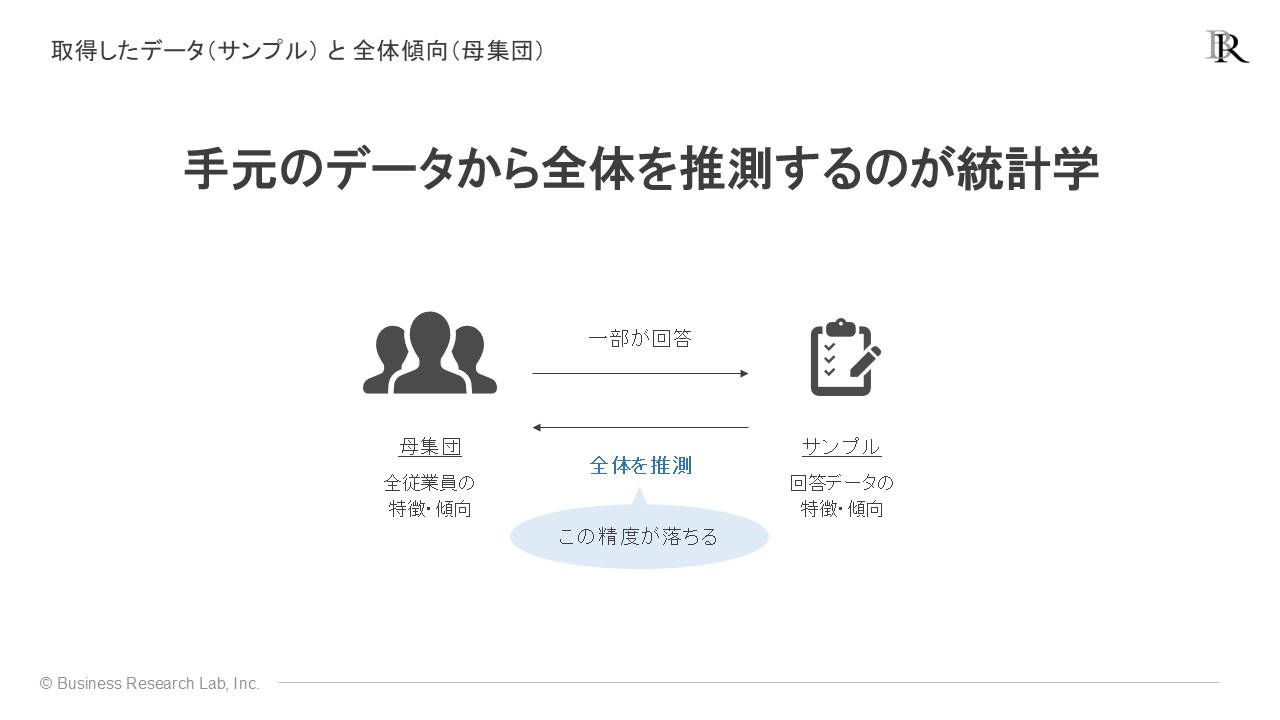
「サンプルサイズ」とは、分析に用いるデータの件数・回答者の人数を指します。サーベイで集めたデータセットの大きさということです。このサンプルサイズがなぜ重要かというと、データ分析の精度が変わるからです。直感的な理解と一致しますが、サンプルサイズが大きい、言い換えると回答者が多いほど、分析の精度は高まります。例えば、100名が所属する会社で、10名のデータから全体の傾向を推測するより、90名のデータを用いる方が、より正確に組織全体の実態を捉えられます。
逆に、サンプルサイズが小さいと分析の精度が落ち、分析結果が組織全体の傾向を指す母集団とは異なる特徴を示してしまう可能性が高まります。統計学では、サーベイで取得した全体の一部であるサンプルの情報から、組織全体を表す母集団の状態を推測します。サンプルサイズが小さいと、この推測の精度そのものが落ちてしまうのです。
具体的には、サンプルサイズが小さいと主に2種類の分析精度の問題が生じます。ひとつは、平均や相関といった数値の推定精度に問題が生じ、分析で示される具体的な数値が不正確になります。もう一つは有意性検定の検証精度の問題で、「統計的に有意か」の検証精度が落ち、組織の実態とは異なる結果が示されやすくなります。
「分析の精度」を掘り下げる:統計学的な視点
1. 「具体的な数値の推定精度」の問題
ここからは、先ほど挙げた2つの問題について、統計学的な背景をより詳しく見ていきます。サーベイのデータを集計・分析すると、平均値や割合、相関係数など様々な統計指標が算出されます。サーベイを行ったら、多くの方がまず着手するデータ分析はこれでしょう。しかし、サンプルサイズが小さいと、これらの指標が組織全体の真の傾向とは異なる値を示しやすくなります。
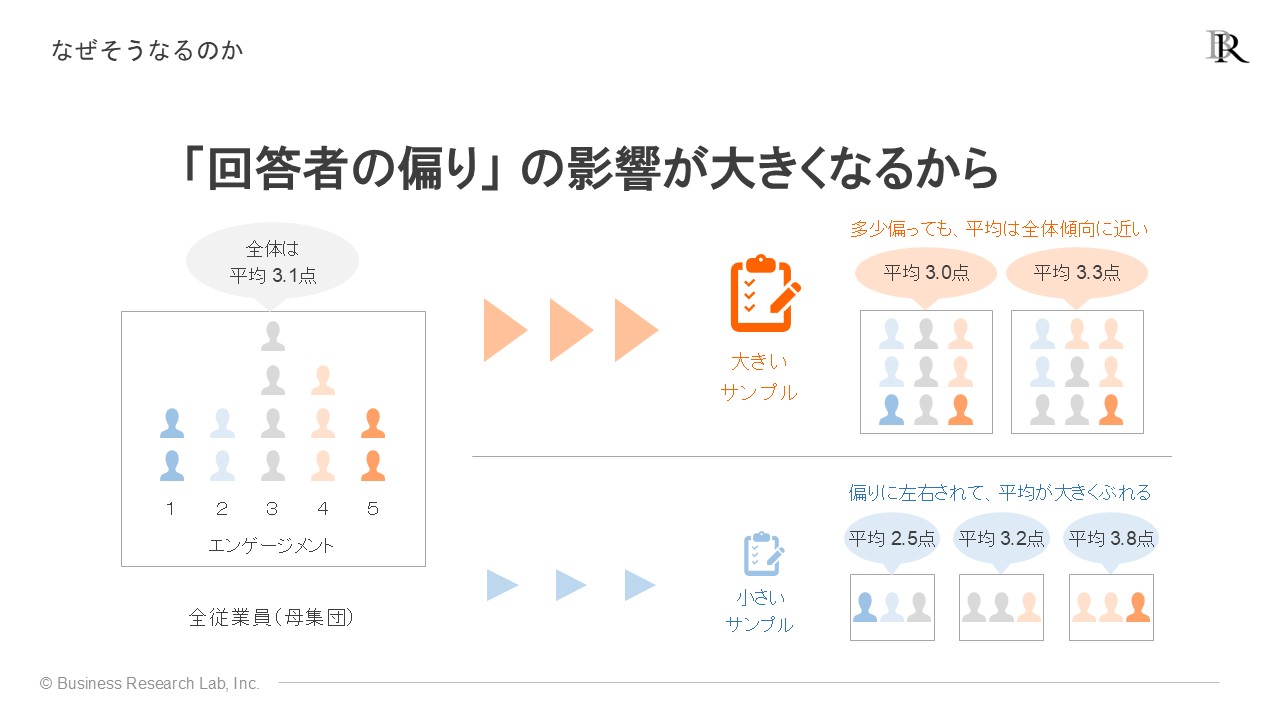
この現象は、回答者の偏りの影響が大きくなるために起こります。例えば、少人数のサンプルだと、偶然エンゲージメントが高い人ばかりが集まったり、逆に低い人ばかりが集まったりするだけで、平均点が大きくぶれてしまいます。一方、サンプルサイズが大きければ、多少の偏りがあっても平均化され、結果は全体の傾向に近い値に落ち着きます。
このように、集計値などの結果がサーベイごとに偏る「揺らぎ」の大きさは、統計学では「標準誤差」と呼ばれる指標で評価されます。標準誤差は、以下の式で計算されます。
SE = SD / √N(SE:標準誤差,SD:標準偏差,N:サンプルサイズ)
この式の分母にサンプルサイズ(N)があることからわかるように、サンプルサイズが小さいほど標準誤差は大きくなり、算出される値の不正確さが増すのです。標準誤差が大きいとサーベイごとの結果が大きくばらつくことを表し、小さければサーベイごとの結果があまり変わらないことを表します。
2. 「統計的検定の精度」の問題
加えて、サンプルサイズが小さいと「統計的に有意でない」結果が出やすくなります[1]。本来は効果のある施策だったとしても、サンプルサイズが小さいという理由だけで「有意な差はない」と結論付けられてしまうリスクがあるのです。
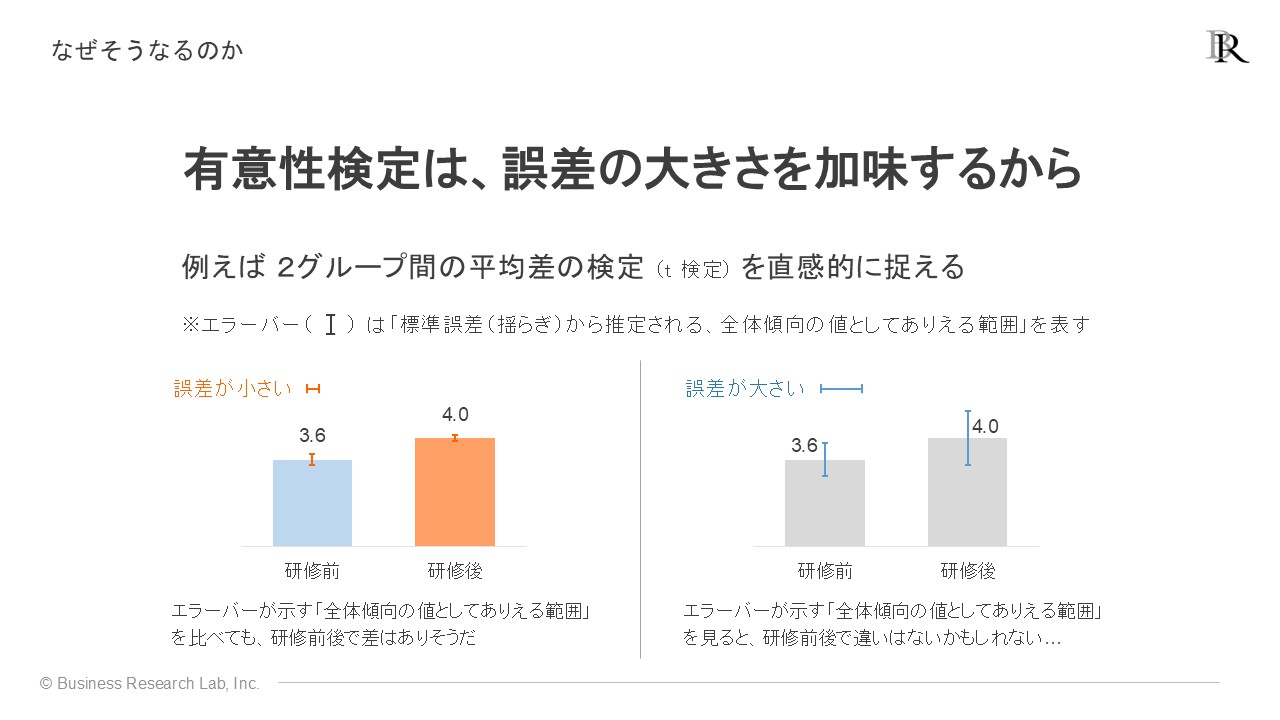
これは、統計的に有意か否かを検証する有意性検定が、前述の「誤差の大きさ」を計算に加味するためです。誤差が大きいと、見かけ上の差が偶然に生じる範囲内だと判断されやすくなり、結果として「有意な差がある」とは言えなくなってしまいます。
棒グラフにおいてよく用いられるエラーバーで、誤差の大きさを加味した有意性検定を捉えると、上の図のようになります。研修前後で3.6点から4.0点と同じ点数上昇が見られたとしても、誤差が大きくエラーバーが長い状態だと「取得したデータにおける平均は3.6点から4.0点と上昇して見えるが、揺らぎが大きいため確実な差とは言い難く、有意な差があるとは言えない」と判断されやすくなるわけです。サンプルサイズが小さいと誤差が大きくなるため、エラーバーが長くなりこの問題が生じやすくなります。
この話題に関連して、統計的に有意か否かを正確に判定する統計的な性能は「検出力」という指標で評価されます。検出力とは、本来捉えたい母集団で差がある指標を、実際に測定した手元のデータで「有意な差がある」と正しく見抜ける確率のことです。
サンプルサイズが小さいとこの検出力が落ちてしまい、有意な差を正しく見抜けなくなります。そのため、サンプルサイズが小さいデータで統計的に有意な差が出なかったとき、「本当に差がなかった」のか、「本当は差があるのに、検出力が低いために有意差が出なかった」のか、区別できなくなる問題が生じます。
検出力の話題を広げると、逆にサンプルサイズが大きすぎることで生じる難点も見えてきます。サンプルサイズが大きいほど検出力が高くなるわけですが、検出力が高すぎると、実質的に意味のないごくわずかな差まで「統計的に有意」と判断してしまう問題が生じます。例えば、1万人のデータがあれば、エンゲージメントスコアが0.01点上がっただけでも「統計的に有意な差がある」と示される可能性があります。
サンプルサイズがとても大きいと、どんな分析でも「統計的に有意」な結果になり、検定の意味が損なわれることがあります。この問題を考慮すると、サンプルサイズが小さいのは問題ですが、逆に無理に多くの回答者を集めてサンプルサイズをとにかく大きくするメリットは薄いといえます。
むしろ、サンプルサイズを集める過剰な努力により、回答の質を低下させるリスクも考慮すべきでしょう。回答者を何とか増やそうと頻繁にリマインドを送り回答を半ば強要してしまうと、適当な回答が増えたり「回答が監視されている」と忖度したポジティブな回答が増える懸念があります。
従業員の人数が多く自然と大きなサンプルサイズが集まりやすい企業や、すでに多くのサンプルサイズを集めてしまい、検出力が高すぎる懸念がある場合は、有意性検定の結果ではなく、「効果量」に注目するのが有効です。効果量は、差や関連の「大きさ」を統計的に一律化された基準で示す指標です[2]。
サンプルサイズが大きいとたいていの有意性検定は「統計的に有意だ」という結果を示しますが、効果量はそれと関係なく「差の大きさは、統計的にこのくらいの大きさと評価できる」と結果を示すため、問題なく分析結果を検討できます。
「ちょうどいい」サンプルサイズの考え方
それでは、少なすぎず多すぎない、適度なサンプルサイズはどのように考えれば良いのでしょうか。ここでは2つのアプローチを紹介します。
1. 具体的な数値の精度(標準誤差)から計算する方法
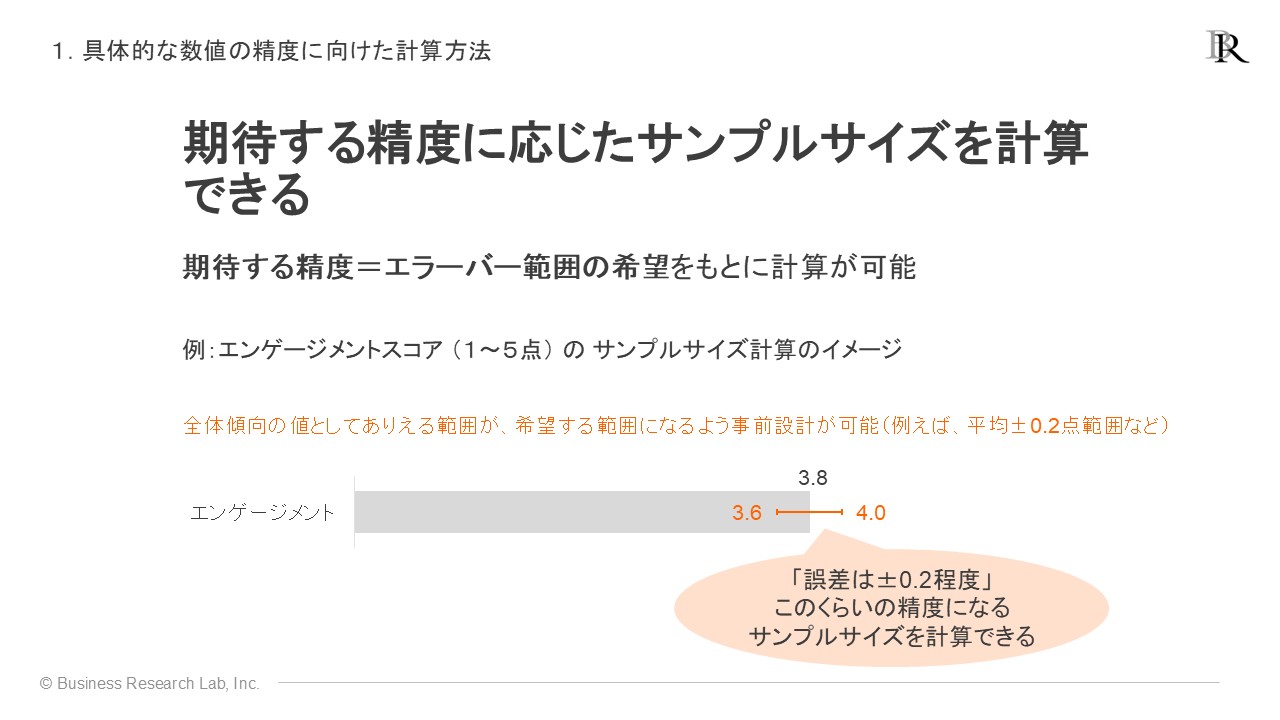
これは、誤差の大きさに関して事前に「許容できる誤差の範囲」を決めるアプローチです。誤差の範囲、言い換えれば分析結果に期待する精度から逆算して、必要なサンプルサイズを求めることができます。
この計算には、先の「許容できる誤差の範囲」を表す希望する範囲aと、精度を計算したい指標におけるデータのばらつきの指標である標準偏差(SD: Standard Deviation)を決める必要があります。希望する範囲aは、上の図のように「サーベイで示される平均などの値に対して、本来の値に対する推定精度は誤差±0.2点」としたときの誤差の幅(-0.2~+0.2)である、a = 0.4点です。標準偏差の値は、過去のサーベイデータで算出した値を参照するなどして決めます。
そのようにして決めた2つの値を以下の式に代入することで、目標の精度を達成できるサンプルサイズを算出できます。
N = (1.96×SD / a)2(N:必要なサンプルサイズ,SD:標準偏差,a:希望する範囲)
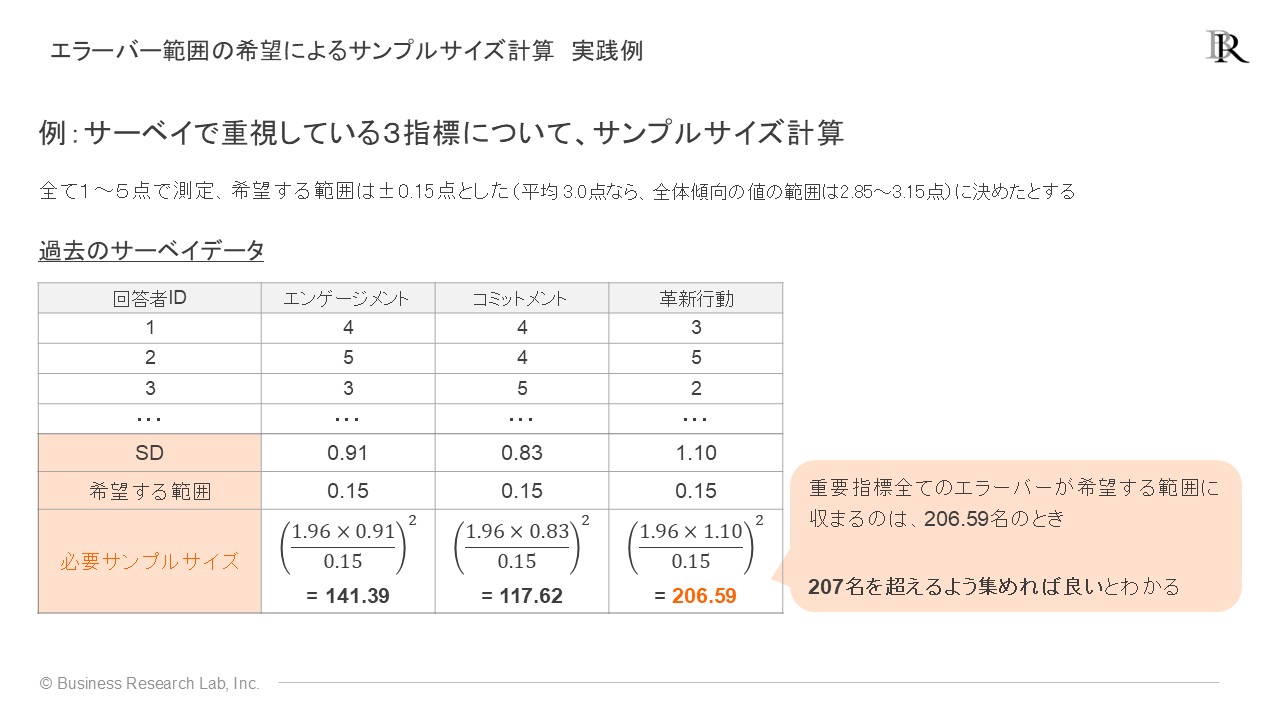
架空データを用いて、必要なサンプルサイズを決めるプロセスを見てみましょう。例えば、サーベイにおいて重要と位置付けた指標としてエンゲージメント、コミットメント、革新行動といった指標がある場合、下の図のようにそれぞれの指標で必要なサンプルサイズを計算します。その上で、最も大きいサンプルサイズが算出された指標に合わせてサーベイの回答者数を確保すれば、すべての指標で目標の精度を満たすことができます。
2. 分析手法が要求するサンプルサイズから考える方法
もう一つの方法は、分析手法に要求されるサンプルサイズに応じて決定するアプローチです。重回帰分析や因子分析といった応用的な分析手法には、分析結果を安定させるために推奨されるサンプルサイズの目安があります。サーベイのデータにおいて実施したい分析が決まっている場合、その手法に応じたサンプルサイズを確認し、それを目指して回答者数を確保するのも一つの考え方です。
当社の分析コラムでは様々なデータ分析手法を解説していますが、そのほとんどで「要求されるサンプルサイズはどのくらいか」を記載しています。ここに示しているもの以外に気になる分析があれば、ぜひお調べいただければお役に立つかと思います。
調査設計と結果解釈の注意点
回答率だけでなく「誰が回答していないか」にも注目する
藤井:
サーベイの実施において、サンプルサイズが小さいことには、統計的な問題だけでなく、実践的な問題も伴います。例えば、回答率が低いと経営層の納得を得にくかったり、特定の部署の課題を見落としてしまったりする可能性があります。
ここで注目したいのが、「回答していない人は誰で、なぜ回答していないのか」という視点です。例えば、特定の部署や属性で未回答者が多い場合、そこには「回答しにくい何らかの障壁」が存在する可能性があります。
その背景には、自分の意見を表明すると不利益を被るかもしれないと感じ、意図的に発言を控える「組織沈黙」のような現象が隠れているかもしれません[3]。回答率という数字の裏側にある組織の課題を示唆する重要なサインを見逃さないことが大切です。
回答の「質」を確保できているか
サーベイでは、回答の「量」だけでなく「質」も重要です。「自分の回答が特定されるのではないか」という不安(評価懸念)や、「よく見られたい」という気持ち(社会的望ましさ、など)は、従業員が本音で回答することを妨げます[4][5]。記名式であったり、部署の人数が極端に少なかったりする場合、匿名性が担保されにくいと感じ、回答が歪んでしまうリスクがあります。
無理に回答を催促するよりも、調査の目的や結果の活用方法を丁寧に説明し、安心して協力してもらえるような配慮が、結果的に質の高いデータを集めることにつながります。
解釈するときの「心のクセ」に注意する
集まったデータを解釈する私たち自身にも、注意すべきバイアス(心のクセ)があります。 例えば、手元にある少数のサンプルが、組織全体の典型的な姿を代表しているかのように直感的に思い込んでしまう傾向(代表性ヒューリスティック)や、少ないサンプルから得られた結果でも信頼できると過信してしまう傾向(少数の法則)、自分にとって都合の良い結果が生じる可能性を高く見積もる傾向(希望的観測)などがあげられます[6][7][8]。
こうしたバイアスは、サンプルサイズが小さいことの問題点を過小評価させ、誤った意思決定につながる危険性をはらんでいます。「データがこう示しているから」と鵜呑みにするのではなく、そのデータの偏りや限界を常に意識することが求められます。
サンプルが少ないときの工夫
どうしても十分なサンプルサイズが確保できない場合でも、そのデータが無駄になるわけではありません。例えば、少数の従業員へのインタビューや自由記述式の質問といった定性的な手法を組み合わせることで、量的データだけでは見えてこない、より深いインサイトを得ることが可能です。
このような工夫によって、限られたデータから得られる示唆を最大化することができます。
おわりに
本セミナーでは、サーベイにおけるサンプルサイズについて、統計的な理論と実践的な注意点の両側面から解説しました。 サンプルサイズは、少なすぎると分析の精度が落ちてしまい、逆に多すぎても結果の解釈を誤らせる可能性がある、非常にデリケートな問題です。
サーベイの目的や実施したい分析、求める精度などを総合的に考慮し、「ちょうどいい」サンプルサイズを目指すことが、組織の実態を正しく捉え、有効なアクションへとつなげる鍵となります。
Q&A
Q:部署の人数がそもそも数十名しかおらず、100名以上の回答を得ることができません。どう考えれば良いでしょうか?
能渡:
分析に求める精度、つまり「許容できる誤差の範囲」を少し広めに設定すれば、必要なサンプルサイズは少なくなります。そもそも回収できる人数が少ない場合は推定精度を高めることに限界があるので、その部署の人数に応じた「ちょうどよい精度、ちょうどよい分析手法」を模索することが、一つの考え方と言えます。
藤井:
量的な分析が難しい場合は、インタビューなどの質的なデータを組み合わせることで、解釈を深めることも一案です。
Q:経営層にサンプルサイズの重要性を納得してもらうには、どう説明すれば良いでしょうか?
藤井:
サンプルサイズが小さいことで、「意思決定を誤るリスク」や「特定の部署が抱える重大な課題を見逃してしまうリスク」があることを伝えるのが有効です。 これは経営的な損失に直結する可能性があるためです。
能渡:
逆に、経営層が「サンプルサイズをとにかく多く集めよう」とおっしゃる場合もあります。 分析手法に必要なサンプルサイズに向けて数多く集めるならそれでよいですが、先ほど述べたように集めすぎてもあまり得はありません。こんな事態に対処するには、経営層にサンプルサイズを集めすぎることの弊害や、無理な催促が回答の質を低下させるリスクも併せて伝え、「適切な人数」を目指すことの重要性を説得するのが良いでしょう。全体傾向を正確に把握して打ち手を考えたいだけならば、とにかくサンプルサイズを増やすよう躍起になる必要は薄いはずです。
Q:従業員数が多いため、サーベイのサンプルサイズが多くなる傾向があります。どのように扱うのが望ましいですか?
能渡:
サンプルサイズが大きい問題は、サンプルサイズが大きいことそれ自体よりも、「サンプルサイズを何とか多く集めよう」と無理をすることで回答者に悪影響が出る問題が大きいです。そのため、自然とサンプルサイズが多く集まる状況はその影響が小さいと考えられ、特に問題はないと言えます。なお、集計や分析においては先ほど解説で言及したように、有意性検定はあまり参考にならないと割り切り、「効果量」など別の指標に注目するのが有効です。
藤井:
注意点として、データが多すぎるからといって、分析者の都合で恣意的に一部のデータを抽出して分析することは、結果を歪めるため避けるべきです。
Q:450名の会社で、アンケートの回答率が毎回20%強です。この数字をどう考えれば良いでしょうか?
能渡:
一部の方しか回答されていない事態は、強い満足や不満など、強い意見を持つ人たちに回答者が偏っている可能性が考えられます。 こうした状況では、全体の傾向というよりは、極端な意見を持つ層の声としてデータを捉える方が適切かもしれません。 回答率を上げるには、「皆さんの回答がきちんと活用される」とサーベイに回答するメリットを伝え、協力の動機を高める施策を行うことが重要です。
脚注
[1] 「統計的に有意」については、当社コラム『人事のためのデータ分析講座「統計的に有意」を学ぶ(セミナーレポート)』をご覧ください。
[2] 効果量や、効果量と有意性検定の違いについては、下記の当社コラムをご覧ください。
[3] Morrison, E. W., & Milliken, F. J. (2000). Organizational silence: A barrier to change and development in a pluralistic world. Academy of Management review, 25(4), 706-725.
[4] Crowne, D. P., & Marlowe, D. (1960). A new scale of social desirability independent of psychopathology. Journal of Consulting Psychology, 24(4), 349–354.
[5] Leary, M. R. (1983). A brief version of the Fear of Negative Evaluation Scale. Personality and social psychology bulletin, 9(3), 371-375.
[6] Tversky, A., & Kahneman, D. (1974). Judgment under Uncertainty: Heuristics and Biases: Biases in judgments reveal some heuristics of thinking under uncertainty. science, 185(4157), 1124-1131.
[7] Tversky, A., & Kahneman, D. (2014). Belief in the law of small numbers. In A Handbook for Data Analysis in the Behaviorial Sciences (pp. 341-349). Psychology Press.
[8] Bastardi, A., Uhlmann, E. L., & Ross, L. (2011). Wishful thinking: Belief, desire, and the motivated evaluation of scientific evidence. Psychological science, 22(6), 731.
登壇者

藤井 貴之 株式会社ビジネスリサーチラボ マネージャー
関西福祉科学大学社会福祉学部卒業、大阪教育大学大学院教育学研究科修士課程修了、玉川大学大学院脳情報研究科博士後期課程修了。修士(教育学)、博士(学術)。社会性の発達・個人差に関心をもち、向社会的行動の心理・生理学的基盤に関して、発達心理学、社会心理学、生理・神経科学などを含む学際的な研究を実施。組織・人事の課題に対して学際的な視点によるアプローチを探求している。
 能渡 真澄 株式会社ビジネスリサーチラボ チーフフェロー
能渡 真澄 株式会社ビジネスリサーチラボ チーフフェロー
信州大学人文学部卒業、信州大学大学院人文科学研究科修士課程修了。修士(文学)。価値観の多様化が進む現代における個人のアイデンティティや自己意識の在り方を、他者との相互作用や対人関係の変容から明らかにする理論研究や実証研究を行っている。高いデータ解析技術を有しており、通常では捉えることが困難な、様々なデータの背後にある特徴や関係性を分析・可視化し、その実態を把握する支援を行っている。