多くの企業で組織サーベイが実施されるようになりました。激しい競争環境の中で、従業員の声に耳を傾け、満足度や生産性を向上させることが、企業の持続的な成功に貢献するという認識が広がってきたからかもしれません。

しかし、組織サーベイを実施するだけでは不十分です。得られたデータから洞察を引き出し、実行可能な施策に結びつけることが重要です。多くの人事担当者が、膨大なデータの山を前に途方に暮れているのではないでしょうか。

そこで本コラムでは、組織サーベイのデータ分析に役立つ「探索的因子分析」という手法に焦点を当てます。この手法を使いこなすことで、複雑な従業員の声の中から隠れたパターンを発見することができます。

本コラムでは、架空のデータ例を交えながら解説していきます。探索的因子分析の基本的な考え方から、実践的な活用方法まで、ステップバイステップで案内します。

探索的因子分析とは

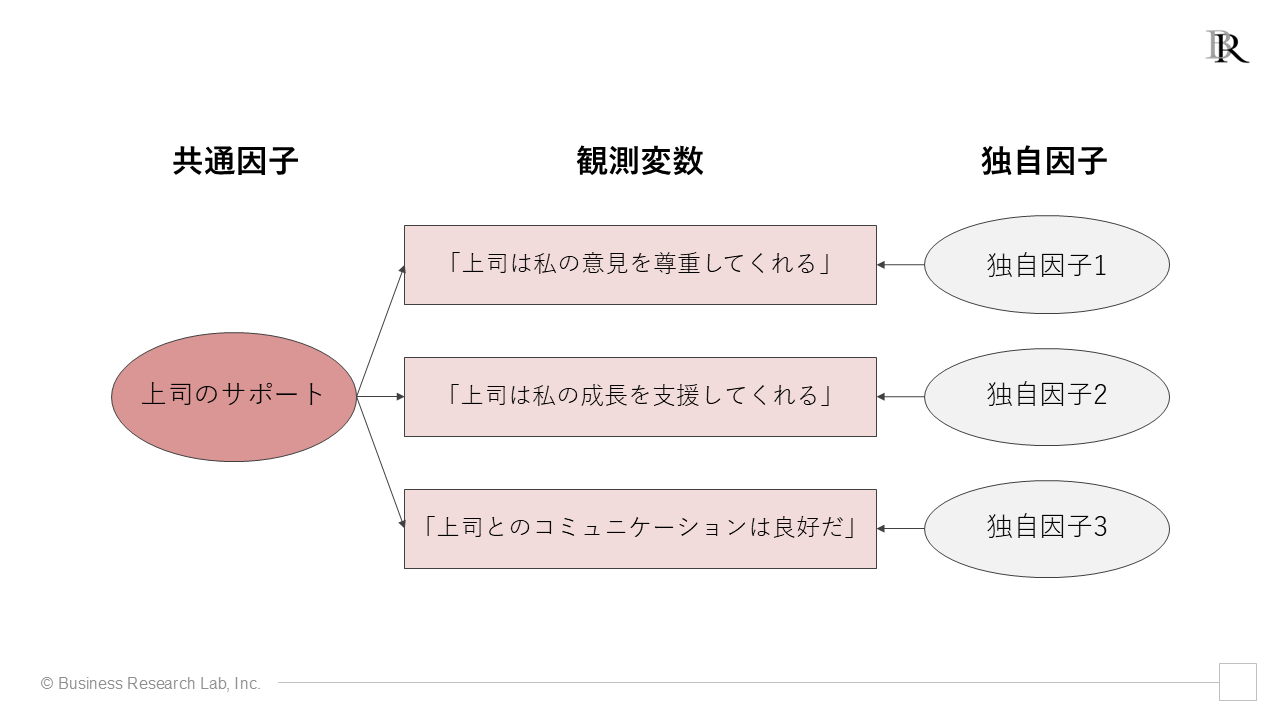
探索的因子分析は、多数の質問項目を分析し、これらの項目が共通して影響を受ける潜在変数（因子）を特定する方法です。各質問項目が複数の因子に依存している可能性を考慮しながら、それらの因子間の共通性を探ります。

例えば、「上司は私の意見を尊重してくれる」「上司は私の成長を支援してくれる」「上司とのコミュニケーションは良好だ」といった質問項目に対する回答が似たような傾向を示すとすれば、これらの項目は「上司のサポート」という共通の因子で説明できるかもしれません。

探索的因子分析を行うことで、人事データ分析の実践上、いくつかのメリットが得られます（理論的なメリットではない点に注意してください）。

• 多くの質問項目を少数の因子に集約することで、全体像を把握しやすくなる
• 直接観測できない概念（例：上司のサポート）を抽出することができる
• 重要な因子に焦点を当てた施策を立案することで、効果的な改善が可能になる

探索的因子分析を理解するうえで、「共通因子」と「独自因子」という2つの考え方を理解しておくと便利です。

共通因子とは、複数の質問項目に共通して影響を与える潜在的な要因です。直接測定することはできませんが、複数の質問項目の回答パターンから推測される、背後にある概念のようなものです。

例えば、「上司のサポート」という共通因子は、「上司は私の意見を尊重してくれる」「上司は私の成長を支援してくれる」といった複数の質問項目に影響を与えていると考えることができます。

対して、独自因子は共通因子によって説明されない、各質問項目を説明する他の要因をまとめたもの（残差）です。これには、例えば、その質問項目特有の要素や測定誤差などが含まれます[1]。

例えば、「上司は私の意見を尊重してくれる」という質問項目の場合、「上司のサポート」という共通因子では説明できない、回答者個人の経験や認識、質問の解釈の違いなどが独自因子に含まれます。

つまり、因子分析においては、各質問項目の回答のばらつきを「共通因子によって説明できる部分」と「固有の部分」に分解します。

前者は、抽出された因子によって説明される分散（データのばらつき）の割合です。この割合が高いほど、その質問項目が抽出された因子によってよく説明されていることを意味します。

後者は、共通因子では説明できない分散の割合です。全体から「因子によって説明できる部分」を引いた値になります。この割合が高いほど、その質問項目が共通因子では十分に説明できない特有の要素を多く含んでいることを指します。

例えば、「上司は私の意見を尊重してくれる」という質問項目の「因子によって説明できる部分」が64%であれば、この項目の回答のばらつきの64%が「上司のサポート」のような因子によって説明されていることになります。残りの36%が「固有の部分」となり、この項目特有の要素や測定誤差などによるものだと解釈できます。

手順とその内容

架空の組織サーベイを例に、探索的因子分析の手順を見ていきましょう。上司のサポートに関する20問のアンケートを例に分析を行います。各質問は5段階評価（1：全くあてはまらない～5：非常によくあてはまる）で回答されており、500名分のデータが得られたとします。

データの確認

データが因子分析に適しているかを確認します。まず、サンプルサイズをチェックします。一般的に、質問項目数の5～10倍程度のサンプルサイズが望ましいとされています[2]。分析結果の安定性を確保するために必要な回答者数のことです。今回の例では20問に対して500名分のデータがあるため、サンプルサイズは十分と考えられます。サンプルサイズが小さいと、結果が不安定になったり、結果の再現性が低下したりする可能性があります。

続いて、変数の性質をチェックします。因子分析には、基本的には連続的なデータが推奨されますが、リッカート尺度のデータも因子分析に使用することが可能です。ただし、リッカート尺度データを用いる場合、そのデータが厳密には順序尺度であり、間隔尺度として扱う際には一定の仮定が必要であることを留意すべきです[3]。

因子数の決定

抽出する因子の数を決定します。因子数の決定は、複数の統計的手法を組み合わせて行うと良いでしょう。

MAP（Minimum Average Partial）法

MAP法は、適切な因子数を決定するための統計的な方法の一つです。この方法は、データの構造をできるだけ簡潔に説明しようとします。因子の数を増やしていったとき、質問項目間の関係がどれだけ説明されるかを計算します。これ以上因子を増やしてもあまり説明力が上がらない点を見つけ出し、その時点での因子数を提案します。この方法は、因子数を少なめに見積もることが特徴です。

例えば、MAP法によって4因子が提案されたとします。これは、4つの因子でデータの主要な特徴を捉えることができることを示唆しています。

平行分析

実際のデータから得られた固有値と、同じ大きさのランダムデータから得られた固有値を比較します。固有値とは、各因子がデータの分散をどれだけ説明できているかを示す指標です。実データの固有値がランダムデータの固有値を上回る因子数を採用します。この方法は適度な因子数を提案するものです。

対角SMC平行分析

これは平行分析の一種であり、ランダムデータの生成に際して、多変量正規分布の相関行列の対角要素として重相関係数の2乗を用いる点が特徴です。ここでの重相関係数とは、ある質問項目を従属変数、その他の全ての質問項目を説明変数として行う重回帰分析において得られる、決定係数(R^2)の平方根を取った指標です。実際の質問項目の得点と重回帰分析のモデルで予測された得点の相関係数になります。

これによって、変数間の関連性をより正確に反映した因子数を提案します。この方法は、特に因子数を多めに見積もる特徴があります。

 これらの方法を用いた結果が次のようになったとしましょう。

• MAP法：3因子
• 平行分析：4因子
• 対角SMC平行分析：5因子

この場合、まずは平行分析が提案する4因子解を試してみます。もし4因子解でうまく解釈できない場合は、3-5因子の範囲で因子数を設定した分析を試し、最も解釈しやすい結果を採用すると良いでしょう[4]。

なお、因子数の決定には、統計的手法に加えて、理論的な背景や調査の目的を考慮することが不可欠です。統計的手法としては、MAP法や平行分析などを用いることができますが、これらはあくまで指標です。最終的な因子数の選定には、分析者がデータの性質や理論的背景を踏まえ、解釈可能性や実務的な妥当性を考慮して判断することが求められます。

今回の例では、4因子構造を採用することにしましょう。

因子の推定

因子数が決まったら、実際に因子を推定します。ここでは最もよく使われる最尤法について紹介します。

最尤法は、データに対して最も可能性の高い因子構造を推定する方法です。この方法は、「もし、この因子構造が正しいとすれば、今回得られたようなデータが観測される確率が最も高くなる」という考え方に基づいています。

分析では、コンピュータが様々な推定値を試し、最もデータにフィットする（データをよく説明できる）値を選び出します。これは、パズルのピースをいろいろな組み合わせで試して、できる限りぴったりとはまる配置を見つけ出すようなイメージです。

このプロセスの中で、各質問項目と各因子の関連の強さを示す「因子負荷量」が計算されます。因子負荷量は-1から+1の値をとり、絶対値が大きいほどその項目とその因子の関連が強いことを示します。

例えば、「上司は私の業務上の問題解決を手伝ってくれる」という質問項目が「道具的サポート」という因子に0.7の因子負荷量を持っていれば、この項目は「道具的サポート」因子と強く関連していると解釈できます。

因子軸の回転

続いて、因子軸の「回転」について考えます。探索的因子分析では、単純構造が望ましいとされています。単純構造とは、各項目が特定の因子に強く関連し、それ以外の因子との関連がほとんどない状態を指します。このような結果が得られると、因子の解釈が容易になり、後続の分析もシンプルになります。

しかし、最尤法などによって得られた因子構造は、必ずしも単純構造になっているとは限りません。因子分析では、単純構造に向けて因子軸を回転する技術があります。

回転とは、因子負荷行列に一定の制約を加えたうえで、その構造を変形させることにより、より解釈しやすい因子構造を得るための手続きです。回転を行うことで、単純構造に近い、より明瞭な因子の解釈が可能になります。イメージとしては、立体的な空間に配置された質問項目群を、最もきれいに見える角度から眺めるようなものです。

例えば、「上司は私の業務上の問題解決を手伝ってくれる」という質問項目が、回転前は複数の因子に中程度の関連を示していたとします。回転によって、この項目が「道具的サポート」因子に強く関連し、他の因子との関連が弱くなるように調整されます。各因子の意味がより明確になり、解釈がしやすくなります。

回転法には次の2種類があります。

• 直交回転：因子間に相関がないと仮定し、因子を互いに独立したものとして解釈する方法。バリマックス回転が代表的です。
• 斜交回転：因子間の相関を考慮し、因子が相互に関連している可能性を考慮する方法。近年はオブリミン回転がよく用いられます。

実際のデータ分析では、斜交回転の方がより現実的な仮定となる場合が多くあります[5]。たとえば、「上司からのサポート」に関する複数の側面には、ある程度の関連性があることが予想され、因子間の相関を認める斜交回転が適しています。ここでは、オブリミン回転を用いることにします。

結果の解釈

回転後の因子パターン行列を見ながら、各因子の意味を解釈していきます。因子パターン行列とは、各質問項目の各因子に対する因子負荷量を表にしたものです。今回は、因子負荷量の絶対値が0.4以上の項目がその因子に強く関連していると判断することにします。

因子パターン行列の読み方を、架空の数値を用いて説明します（わかりやすさを重視し、一部、少し大げさな数値にしています）。

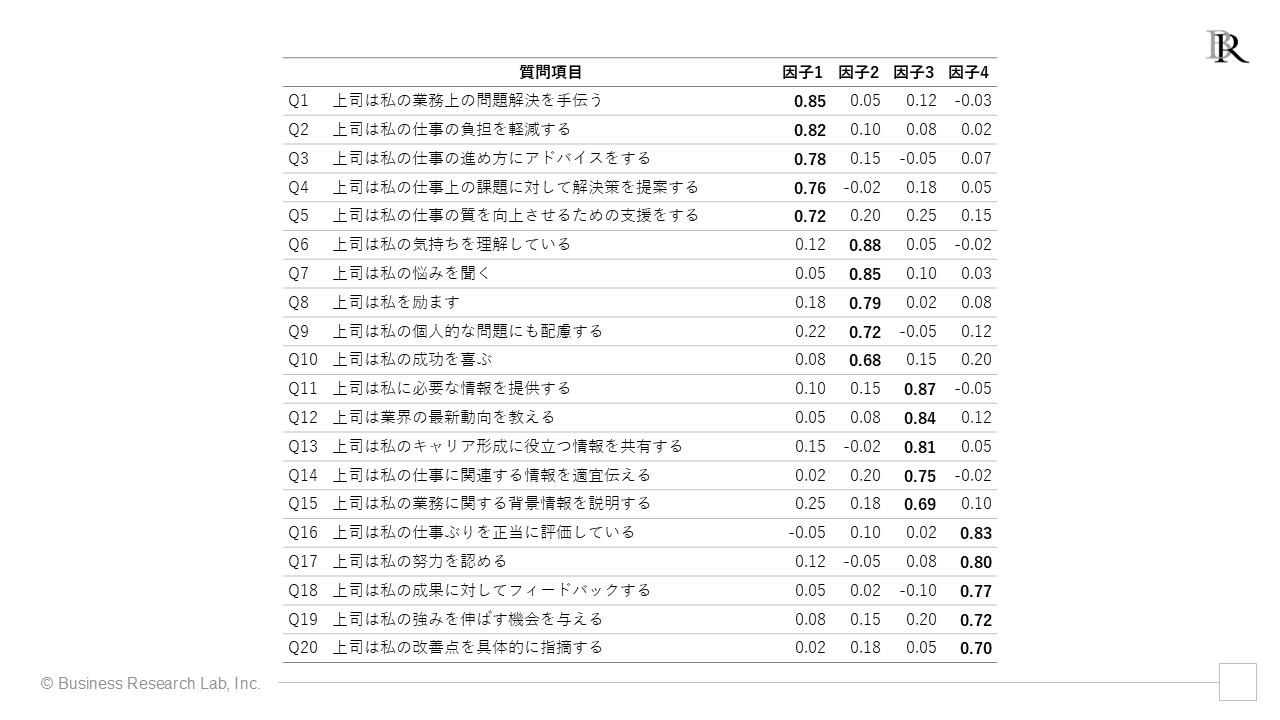
因子パターン行列において、各行は質問項目を、各列は因子を表しています。表の中の数値が因子負荷量です。これは各質問項目と各因子の関連の強さを示しています。太字で示された数値（今回は0.4以上）は、その項目がその因子に強く関連していることを表しています。

例えば、Q1は因子1に0.85という高い負荷量を示していますが、他の因子への負荷量は低いことがわかります。これはQ1が主に因子1を測定していることを意味します。同様に、Q6～Q10は因子2に、Q11～Q15は因子3に、Q16～Q20は因子4に高い負荷量となっています。

各因子に関連する項目群を慎重に検討し、その因子が何を表しているのかを解釈します。ただし、この解釈は主観的であり、複数の解釈が存在する可能性があります。

この結果から、4つの因子を解釈することができます。

• 因子1-道具的サポート（仕事上の具体的な支援）：「上司は私の業務上の問題解決を手伝う」「上司は私の仕事の負担を軽減する」などの項目が高い負荷量を示しています。これらは上司による具体的な業務支援を表しています。
• 因子2-情緒的サポート（精神的な支援）：「上司は私の気持ちを理解している」「上司は私の悩みを聞く」などの項目が高い負荷量を示しており、これらは上司による心理的な支援を意味しています。
• 因子3-情報的サポート（情報提供による支援）：「上司は私に必要な情報を提供する」「上司は業界の最新動向を教える」などの項目が高い負荷量となっています。上司による情報提供を通じた支援を捉えた因子と言えます。
• 因子4-評価的サポート（適切な評価とフィードバック）：「上司は私の仕事ぶりを正当に評価している」「上司は私の努力を認める」などの項目の負荷量が高く、上司による適切な評価やフィードバックを指していることがわかります。

このように、因子分析によって20の質問項目を4つの意味のある因子にまとめることができました。「上司のサポート」という複雑な概念を構造化して捉えることが可能になります[6]。

加えて、今回の分析では斜交回転（オブリミン回転）を用いているため、因子間相関にも注目すると良いでしょう。例えば、次のような結果が得られたとします。

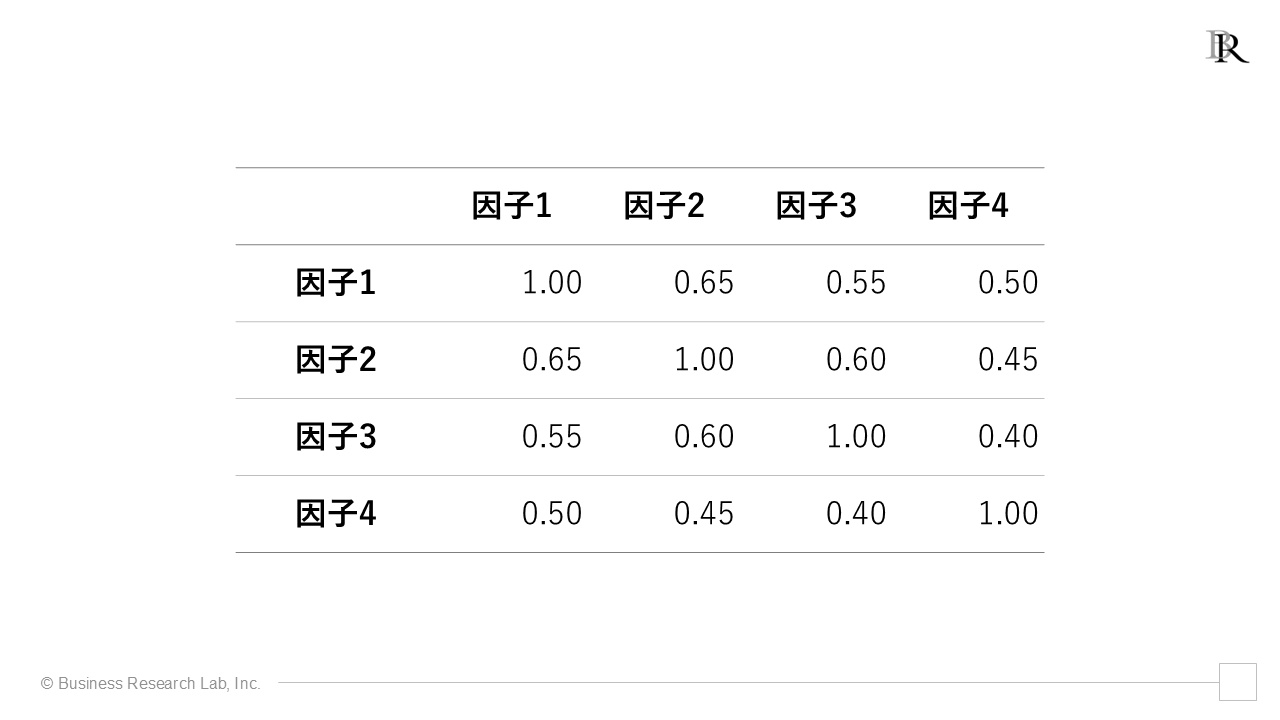
この結果からは、全ての因子間にある程度の相関があることがわかります。特に、因子1（道具的サポート）と因子2（情緒的サポート）の間の相関が0.65と比較的高いことから、上司による具体的な業務支援と心理的な支援は密接に関連していると捉えられます。

以上の通り、探索的因子分析を用いることで、多数の質問項目から少数の因子を抽出し、組織サーベイの結果を効果的に要約することができます。この結果を基に、組織の強みや課題を特定し、より焦点を絞った施策を立案することができるでしょう。

ただし、因子分析は有用なデータ分析手法ですが、その結果はあくまで仮説的なものであり、データに基づく推測に過ぎません。因子の選定や解釈には主観も含まれるため、他の分析手法や追加のデータ検証を組み合わせて結果を裏付けることが重要です。

脚注

[1] 近年の測定モデルでは、そもそも質問項目特有の要素と測定誤差を分けて整理し、独自因子としてまとめない観点を採用することも多いです。一方で、伝統的な探索的因子分析において推定される独自因子は、各質問項目に固有の要因だけでなく、測定誤差も含まれてまとめたものを扱っています。ここで論じる「独自因子」は、この名称を用いる上で伝統的な観点を採用し、「共通因子」で説明できない要素である「残差」すべてを含むものとして捉えるよう説明しています。

[2] ただし、これは厳密な基準ではありません。サンプルサイズが大きいほど結果の安定性は増しますが、データの質、因子の数や強さ、共通性の大きさなど、他の要因も重要です。

[3] データの線形性、共通性、独立性といった条件も確認する必要があります。また、2択（はい・いいえ）などの極端に少ない選択肢の場合は、別の分析手法を検討することが求められます。

[4] このように、MAP法で示される少ない因子数と対角SMC平行分析で示される多めの因子数の間で検討をくり返し、最適な因子解を探る方法を挟み込み法（堀, 2005）と呼びます。

堀 啓造(2005).　 因子分析における因子数決定法—平行分析を中心にして―　香川大学経済論叢, 77(4), 35-70.

[5] かつてはコンピュータの性能上の制約から、計算の容易な直交回転が主に用いられていましたが、現在では計算能力の向上により、斜交回転も容易に実行可能となっており、意図や目的がない限りは斜交回転を用いるのが一般的となっています。

[6] 因子分析の結果を解釈するための他の指標として、因子寄与率や累積寄与率というものもあります。これに関して、斜交回転を採用した因子分析では、因子間に相関を認めるため各因子の説明力に重複が生じ、因子寄与率や累積寄与率を単純に計算したり合計したりすることは難しくなります。そのため、斜交回転を用いた際は、寄与率に関する指標を確認しないことが多いです。

---

執筆者

伊達 洋駆　株式会社ビジネスリサーチラボ 代表取締役
神戸大学大学院経営学研究科 博士前期課程修了。修士（経営学）。2009年にLLPビジネスリサーチラボ、2011年に株式会社ビジネスリサーチラボを創業。以降、組織・人事領域を中心に、民間企業を対象にした調査・コンサルティング事業を展開。研究知と実践知の両方を活用した「アカデミックリサーチ」をコンセプトに、組織サーベイや人事データ分析のサービスを提供している。著書に『60分でわかる！心理的安全性 超入門』（技術評論社）や『現場でよくある課題への処方箋 人と組織の行動科学』（すばる舎）、『越境学習入門 組織を強くする「冒険人材」の育て方』（共著；日本能率協会マネジメントセンター）などがある。2022年に「日本の人事部 HRアワード2022」書籍部門 最優秀賞を受賞。東京大学大学院情報学環 特任研究員を兼務。