探索的因子分析とは何か

上司と部下の関係性によって、パフォーマンスに違いをもたらしているかを把握するため、上司と部下の関係性をとらえる質問項目を作成し、サーベイを行ったとします。回答選択肢は「１．あてはまらない～３．どちらともいえない～５．あてはまる」です。例えば、以下の11項目でサーベイを行ったとします。

• Q1. 上司は私に対して厳しい指摘や叱責を行う
• Q2. 上司は私のミスに対して強く反応する
• Q3. 上司と話すときは言葉を慎重に選ぶ必要がある
• Q4. 上司とは気兼ねなく仕事の話や相談ができる
• Q5. 上司は私の仕事にあまり関心を示さない
• Q6. 上司は私たちの職場を清潔に保つよう努めている
• Q7. 上司は私が困っていても積極的に関与しようとしない
• Q8. 上司は私の話に親身になって耳を傾けてくれる
• Q9. 上司は問題が起きたときだけ強く注意し、それ以外はあまり関与してこない
• Q10. 上司と私は、仕事において対等なパートナーのように感じる
• Q11. 上司とは仕事以外の話も気軽にできる関係だと思う

これら11項目を上司部下の関係性を表す得点として扱い、関係性得点の高さを部署間で比較したり、生産性といった指標との関連を掘り下げて検討したりするかもしれません。

このとき、回答値を単純に合計して関係性得点を出すこともあるでしょう。その際に、今回紹介する統計解析を駆使すれば、データに対してさらに有用な観点を明らかにしていくことができます。例えば、上司と部下の関係性は、実は複数の側面で成り立っているかもしれません。そしてそれぞれの側面によって生産性に与える影響が異なっているとすれば、画一的ではなく、側面ごとに施策を考える必要が出てきます。このコラムで紹介する分析は、このように概念を構成する様々な側面をデータで明らかにすることができます。

先ほど述べた「事前には考えが及んでいなかった、上司と部下の関係性を捉える複数の側面」のような、データとしては直接測定していない、各質問項目の背後にある概念のことを因子と呼びます。サーベイで測定した各質問項目の背後にどういった因子が潜んでいるのか、これを統計的に検証して明らかにする分析が探索的因子分析[1]です。

探索的因子分析とは、様々に測定した質問項目の背後にある因子を、項目の間にある関係性の強さに基づいて探索的に抽出する分析です。探索的因子分析を行うことによって、「Q1. 上司は私に対して厳しい指摘や叱責を行う」や「Q2. 上司は私のミスに対して強く反応する」は同じ因子を背後に持つ質問項目群であるといったことがわかります。

また「Q7. 上司は私が困っていても積極的に関与しようとしない」や「Q11. 上司とは仕事以外の話も気軽にできる関係だと思う」は別の因子を背後に持つ質問項目群であるといったことが、分析で示されます。分析結果から、作成した質問項目の背後にある概念について検討し、サーベイで測定した事柄の理解を掘り下げて組織の実態を深く捉えるヒントを得ることができるのです。

本コラムでは、最初に挙げた「上司と部下の関係性の種類を知りたい」という目的の下でサーベイを行ったという架空の状況を通して、探索的因子分析の分析展開と結果からわかること、分析に関する注意点について説明します。

探索的因子分析の流れ

探索的因子分析を実行する際には、データの特性や分析の目的に合わせて、いくつかの分析設定を分析者が決める必要があります。

それは、「因子数」「因子抽出法」「因子の回転」です。

探索的因子分析は、「測定した質問項目の背後には、いくつの因子がありそうか」を表す因子数を決めることから始まります。因子数とは読んで字のごとく、因子（データから抽出される概念）の個数を指します。先ほどの例に対応させると、「上司部下関係を測定する11個の項目の背後には、いくつの因子がありそうか」、ひいては「11個の項目は何個の概念に分かれそうか」を決めるということです。

この因子数は、分析によって何個に分けるのが適切か判断することができます。その方法のひとつが平行分析です[2]。平行分析は、データから見つかった因子が意味のあるものなのか、ランダムなデータで得られるようなレベルの無意味なものなのかを見極めて因子数を決定する方法です。

平行分析の仕組みを簡単に見ていきます。質問項目の回答データの関連性を分析すると、「その背後に仮定される因子は、それらの関連性をどの程度説明できるか」を表す情報量の指標を算出することができます。情報量が多い因子は質問項目同士の関連性をよく説明しており、「質問項目の背後にその因子がありそうだ」と考えられるわけです。

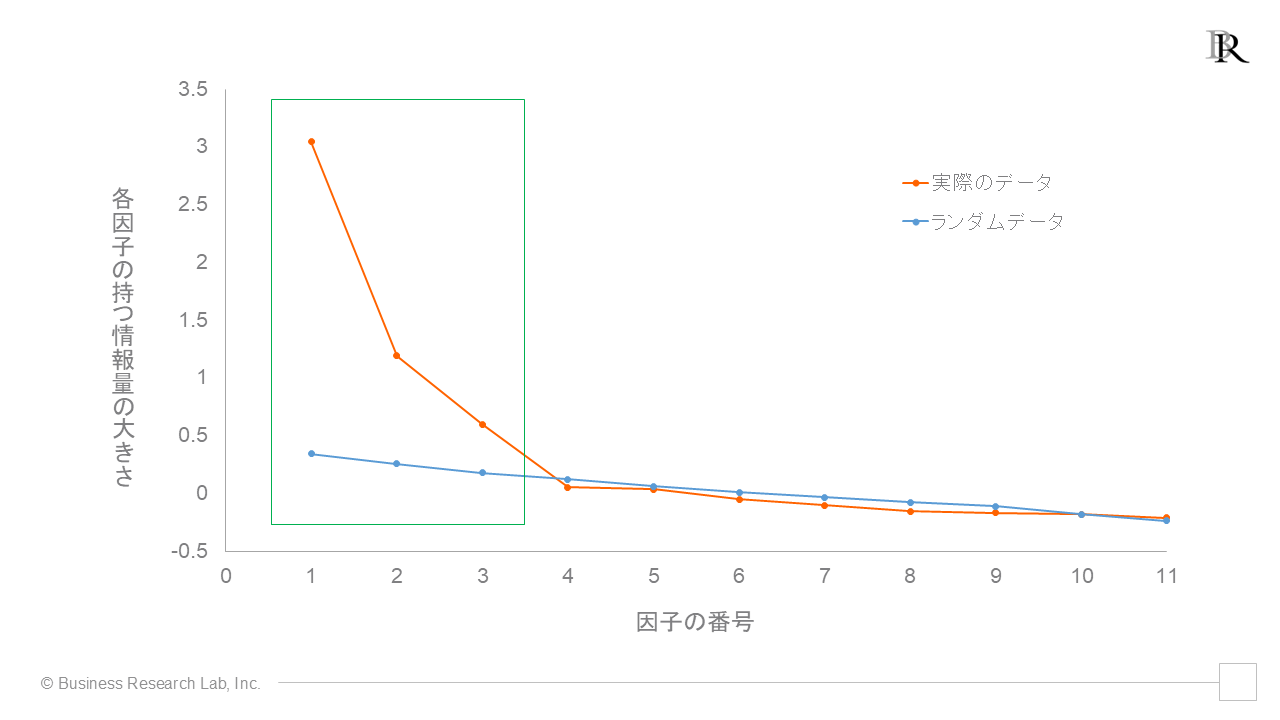
これに対して、ランダムなデータはデータ間に関連性が存在せず、そこに因子を仮定して情報量を計算しても、関連性がないため情報量はほぼ0になると考えられます。この「情報量がほぼない場合のデータ」を基準にして因子数を考えるのが、平行分析のアプローチです。下図は、実際のデータから得られた各因子がもつ情報量(橙色線上の点)と、ランダムなデータから得られた因子が持つ情報量(青線の点)を、それぞれプロットしたものです。図中の緑の枠線に囲まれている部分を見ます。

すると、ランダムなデータから得られる因子が持つ情報量（青色）よりも、実際のデータ（橙色）において大きな情報をもつ因子は3であることがわかります。逆に、緑の枠線外にプロットされている橙色の点は、全て青線よりも下にプロットされていることから、実際のデータにおける4つ目以降の因子は、それらの情報量がランダムなデータから得られた情報量よりも少ない、無意味なものであることがわかるわけです。

[3]

よって今回の上司と部下の関係性について集めた今回のデータを検証した結果からは、因子数を3つと考えることができます。

因子数を決めたら、次は因子の抽出法と回転方法を決める段階に入ります。

抽出法とは因子の抽出に関する統計的な計算方法を指します。上司部下関係を測定する質問項目においては、11個の項目の内、「上司は私の話に親身になって耳を傾けてくれる」と「上司とは気兼ねなく仕事の話や相談ができる」などが一つの因子を構成していそうです。

しかしこれらの項目は、「上司は私に対して厳しい指摘や叱責を行う」といった項目とは別の因子になりそうだ、ということを計算することになります。その計算を統計解析処理の内部でどのように行うか抽出法で決めているわけです。

ここで、その内部の処理を簡単に整理します。因子が合計3つあるとして、1つ目の因子をx軸、2つ目の因子をy軸、3つ目の因子をz軸と考えると、各質問項目はそれぞれの因子とどの程度関連しているかを示す値(因子負荷量)に応じて、この3次元空間上の1点に各質問項目を配置することができます。

またx軸、y軸、z軸は因子軸と呼ばれ、因子軸を原点中心として動かすことで、各質問項目がいずれかの因子軸上のみで0以外の値を持ち、その他の因子軸上では0となるようにする必要があります。これは後述する単純パターンと呼ばれる構造を追求するためです。

探索的因子分析の結果の見方と解釈

ここからは、探索的因子分析を実行した結果を見ていきましょう。上司と部下の関係性について回答を集めた架空のデータに関して、「因子数」：3、「因子抽出法」：最尤法、「因子の回転」：オブリミン回転と設定して分析した結果を示しています。

探索的因子分析の難しいところはここからになります。様々な基準やまとまった因子の内容を分析者が解釈し、調整を加えた再分析を繰り返すことになるからです。場合によっては、因子数を変えたり、回転法を考え直したりすることもあります。その手続きを追ってみましょう。

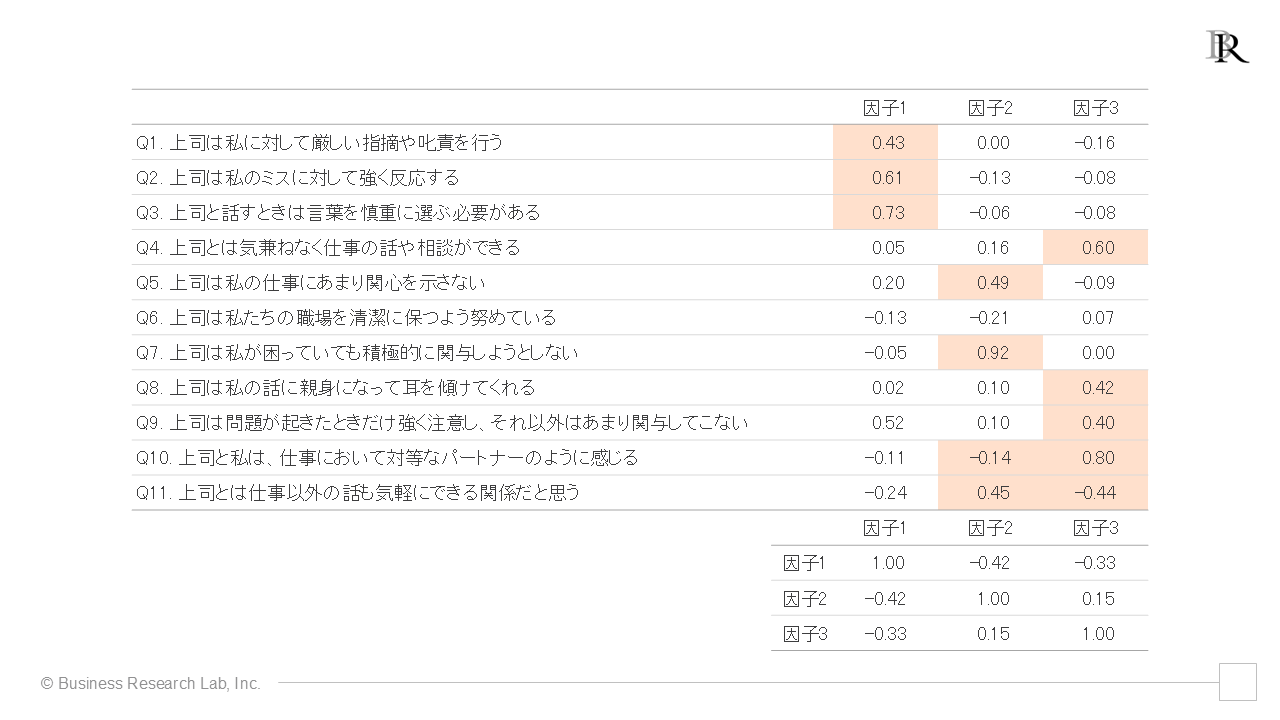
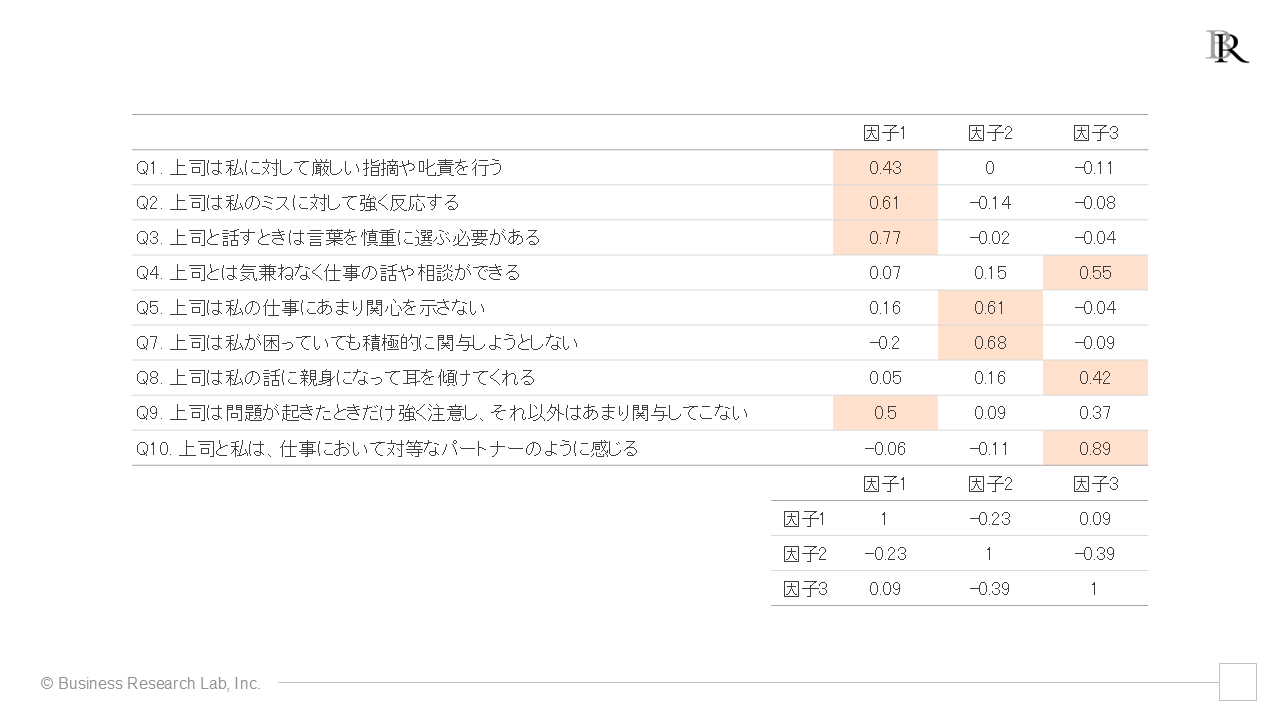
まず、1回目の分析実行による結果です。分析を行ったら、上司と部下の関係性を示す、11個の質問項目群と抽出された因子との関連の強さを示した表が下記のように示されます。最初に注目するのは、出力された表の内、上の大きな表のことです。小さな表については、後で説明します。

上の大きな表内の数値は「因子負荷量」と呼ばれ、その絶対値が大きいほど、因子が質問項目をよく説明していることを意味します。一般的に、この因子負荷の絶対値が0.4、あるいは0.3以上である場合に、「因子がその項目を十分に説明している」と判断します。上の表では、絶対値が0.4以上の箇所に色を付けています。

因子負荷量において、正の値は、「背後にある因子の程度・状態を表すスコアが高いと、その項目の得点も高くなる」傾向を意味します。一方で、負の値は、「因子のスコアが高いと、その項目の得点は低くなる」傾向を示します。

次に注目すべきは、下側の小さな表です。これは、抽出された複数の因子同士がどの程度関連しているかの相関係数を示すものです。相関係数の正の値は「一方の因子のスコアが高いと、他方の因子のスコアも高くなる」傾向を示します。逆に、負の値は「一方の因子のスコアが高いと、他方の因子のスコアは低くなる」傾向を示します。つまり、上の大きな表は、因子と項目の関連性を示し、下の小さな表は、因子と因子の関連性を示しているわけです。

ここで、上司と部下の関係性を示す11個の質問項目群は、おおよそ3つの因子に分かれていることがわかりますが、まだこの段階では、因子がどういうものなのか考えたり、解釈をしたりすべきではありません。各質問項目と抽出された因子との関連の強さを示した表から、結論を導くためには、表が単純パターンという構造を示している必要があります。

単純パターンとは、「どの質問項目においても、どれか一つの因子とだけ強く関連していて（＝因子負荷量の絶対値が0.4以上になる因子が一つだけである）、残りの因子とは関連していない(＝残りの因子との因子負荷量の絶対値が0.4未満になる)」という状態です[7]。単純パターンにあてはまっていない項目を分析から一旦除外し、残りの項目で再度因子分析を実行して、「各質問項目と抽出された因子との関連の強さを示した表」が単純パターン、先ほどの条件に近づいているかを確認します。

このとき、複数の項目を一度に除外するのではなく、一項目ずつ除外していくことが必要です。どの因子とも関連性を示さなかったり、逆に複数の項目が複数の因子と強い関連を持っていたりするということが頻繁に起こります。

このような項目を処理する際には、一度にまとめて除外するのではなく、まず1項目を除外して再度因子分析を実行し、出力された「各質問項目と抽出された因子との関連の強さを示した表」を同じ基準で確認します。その結果、まだ基準を満たさない項目があれば、さらに1項目を除外して再分析を行う、という作業を、単純パターンに近づくまで繰り返していきます。

先ほどの表でこのプロセスを追ってみると、「Q6上司は私たちの職場を清潔に保つよう努めている」はどの因子においても因子負荷量が0.4を下回る小ささであり、いずれの因子とも強い関連性を示していないことがわかります。単純パターンにあてはまっていない項目の中でも、このような全体的に因子負荷量が小さい項目は、初めに除外する必要があります。

どの因子とも関連を示さないということは、他の10項目が捉えている概念、つまり項目の背後にある「上司と部下の関係性」とは異なる概念を捉えているということです。このような事態は質問の焦点が曖昧であったりする際によく起こります。

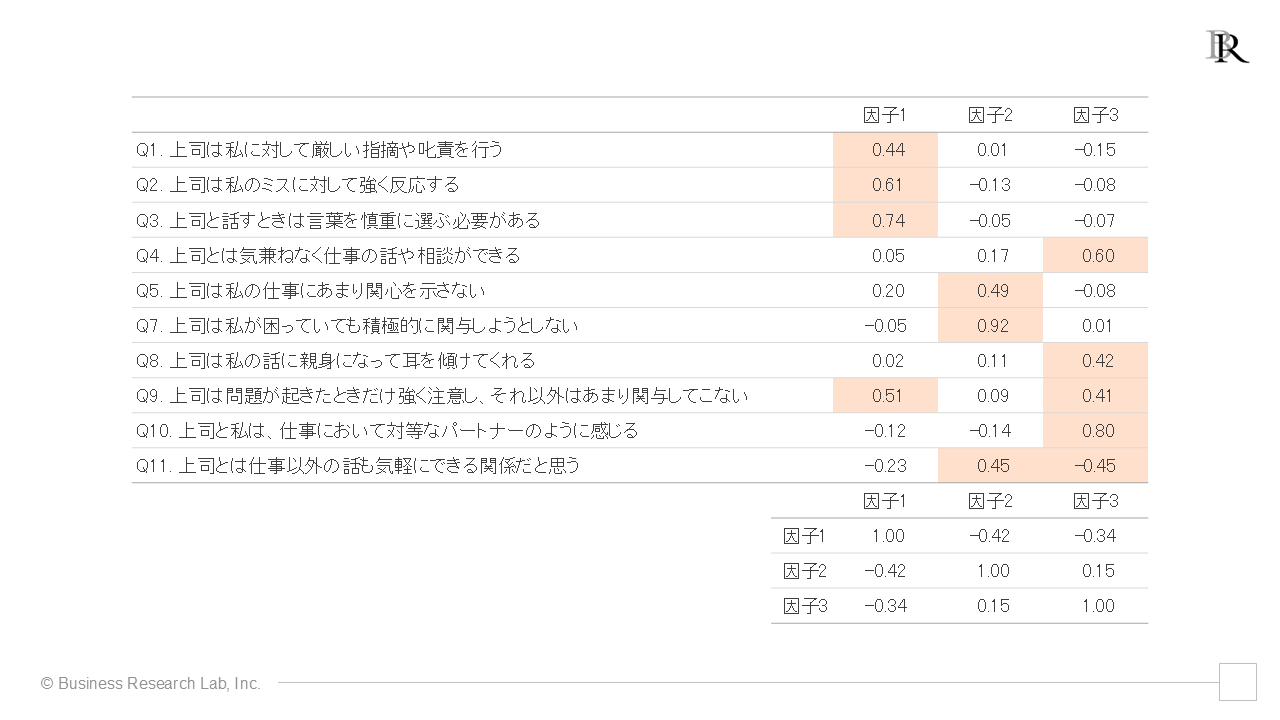
Q6を除外して、再分析した結果は、下図になります。

この結果では、各項目で因子負荷量は全体的に0.4を超えており、少なくともどの因子とも関連が小さい項目はなさそうです。しかし、Q9やQ11を見ると、複数の因子と強い関連を示しています。これらも単純パターンにあてはまっていません[8]。1項目ずつ除外するというルールのもと、Q9 だけ(上図)、およびQ11だけ(下図)除外して再分析した結果を以下にそれぞれ示しました。

Q9を除外した場合

 

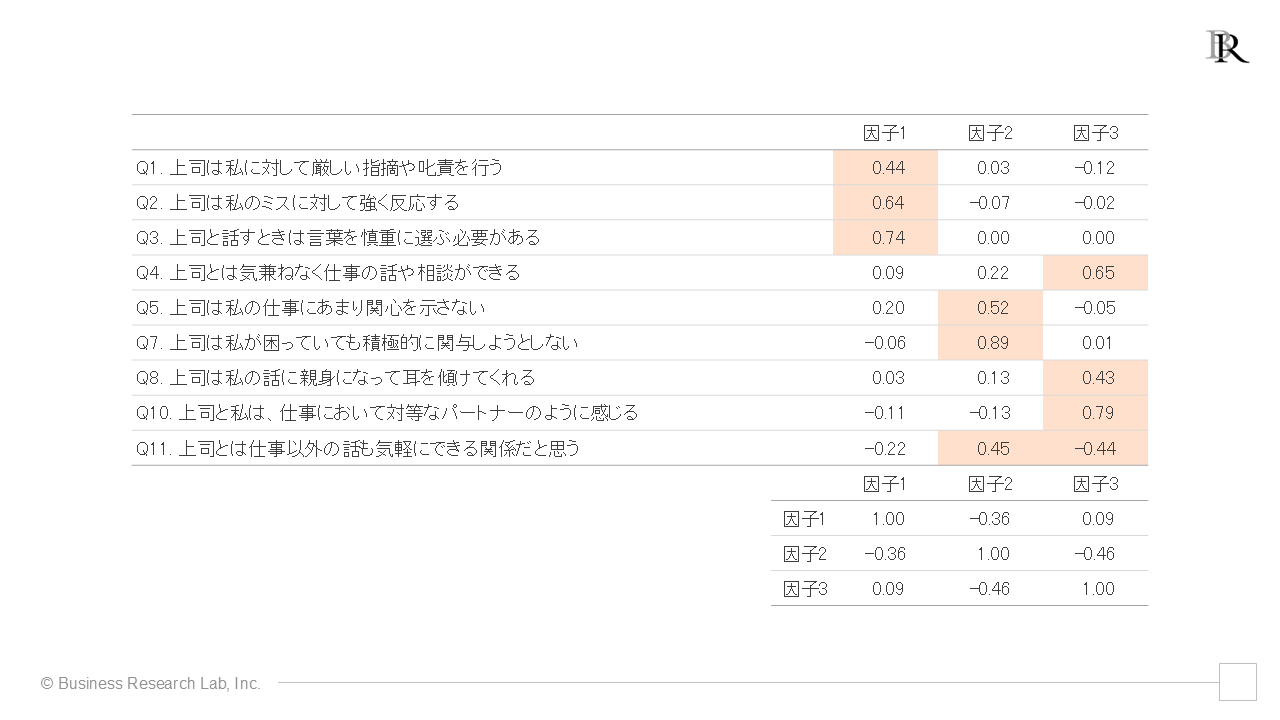
Q11を除外した場合

再び、因子負荷量が0.4以上の箇所に色を付けました。

Q9を除外した場合には、Q11は依然として、複数の因子と強い関連を示していますが、Q11を除外した場合には、0.4以上が強い因子負荷であるという基準のもとでは、Q9を含めていずれの項目も因子負荷が強い値を示すのは1つの因子のみである状態になりました。したがって、ここではQ11を除外した方を採用することにします。

これで、「どの質問項目においても、どれか一つの因子とだけ強く関連していて、残りの因子とは関連していない」、つまり単純パターンとなりました。よって、ようやく因子がなにを表しているのか考える段階に来たことになります。実際、単純パターンであるために、上司と部下の関係性における3つの因子がそれぞれ何をさすのか、解釈しやすい内容のまとまりに仕上がっています。

解釈をやりやすくするため、因子負荷量が大きい順に並べ替えたものが以下の表になります。それに伴い、因子の順序も変えています。

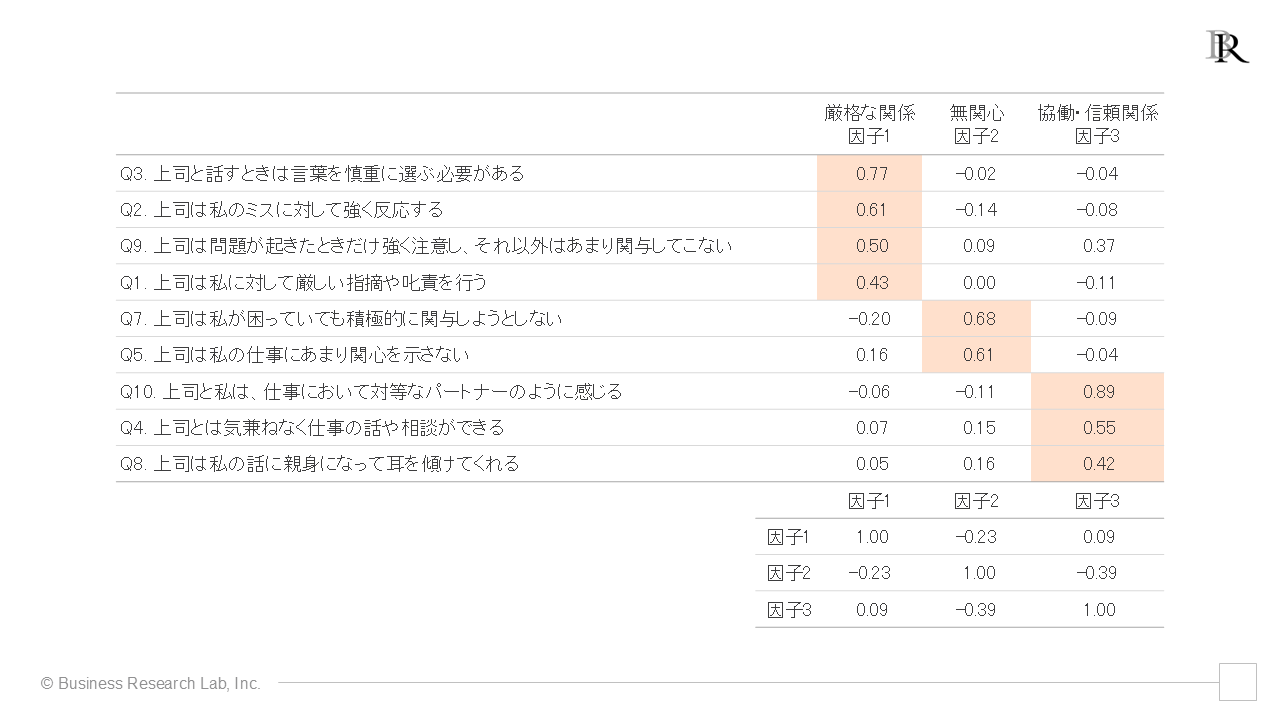
単純パターンにまとめられたら、それぞれの因子が何を表しているか解釈していきます。先に述べた通り、各因子の意味付けは分析者が実践的な経験や学術的な知見・理論を背景に、主観的に解釈する必要があります。

因子1は、「Q2. 上司は私のミスに対して強く反応する」、「Q3. 上司と話すときは言葉を慎重に選ぶ必要がある」、「Q9. 上司は問題が起きたときだけ強く注意し、それ以外はあまり関与してこない」、「Q1. 上司は私に対して厳しい指摘や叱責を行う」といった項目の因子負荷量が大きくなっています。

これら因子負荷量の大きい4項目は、上司が部下に対して一定の距離を保ちつつ、厳格で指導的な姿勢を取ることを示す項目と高い因子負荷を示しています。よって因子1は「厳格な関係」を表す因子と解釈できます。

因子3は、「Q4. 上司とは気兼ねなく仕事の話や相談ができる」、「Q8. 上司は私の話に親身になって耳を傾けてくれる」、「Q10. 上司と私は、仕事において対等なパートナーのように感じる」といった項目の因子負荷量が大きくなっています。つまり、因子3は上司と部下の間にある心理的な近さや信頼・協働姿勢を示す項目と強く関連しています。よって因子3は「協働・信頼関係」と解釈できます。

因子2は、「Q5. 上司は私の仕事にあまり関心を示さない」や「Q7. 上司は私が困っていても積極的に関与しようとしない」といった項目の因子負荷量が大きくなっています。つまり、因子2は、上司の無関心さや放任的な態度を反映する項目と強く関連する因子だと言えます。よって因子2は「無関心」と解釈できます。

このように、各因子において因子負荷量が大きい項目のまとまりを全体的に見てその共通要素を考えることで、因子がどういった概念を表すのかを分析者が解釈していくわけです。

ここで、因子同士の関連性を示す表の下部を見ると、たとえば、「無関心」は「厳格な関係」と「協働・信頼関係」の間に小さな負の相関が示されています。「厳格な関係」や「協働・信頼関係」があると「無関心」が低い対応関係が小さいながらあることがわかります。

また「厳格な関係」と「協働・信頼関係」は相関がほぼ0です。これらの概念間には互いにほとんど関連がなく、上司が部下に厳しく接しながらも温かくサポートする場合もあれば、上司が部下に厳しく接するのみで温かいサポートがないなど、これらの概念には一定の傾向がなく様々な組み合わせがあることがわかります。

以上のように、探索的因子分析を用いることで、測定した項目がどのような概念を捉えているかを統計的に評価し、その概念はどういったものかを捉えることができます。今回挙げた例では、当初11項目で測定しようとしていた「上司と部下の関係性」という漠然とした概念は、3つの関係性のタイプで構成されると解釈することができました。11項目がどういった概念に分かれるか見えていなかったところが、分析で評価できるわけです。

また、分析で示された「厳格な関係」、「協働・信頼関係」、「無関心」いう3つの関連性の側面が、それぞれ具体的にどの質問項目によって測定されているのか、その対応関係を明確にすることができました。目的に応じて測りたい関係性の因子を捉える項目のみをサーベイで用いるといったことも、今後は可能となります。

さらに、探索的因子分析を用いることで、「この質問項目は〇〇を測っているはずだ」という想定が、データと合っているかを検証できます。たとえば「Q6. 上司は私たちの職場を清潔に保つよう努めている」は、上司と部下の関係性の一側面を表すと思われていましたが、今回の分析で抽出された3つの側面とは異なる因子に該当することがわかりました。このように、作成した項目が意図した概念を測定しているか、妥当性を統計的に確認できます[9]。

探索的因子分析の注意点

最後に、探索的因子分析を行う際に注意すべきポイントを3点挙げます。1つ目として、Orçan, F. (2018)[10]がBandalos (2010) [11] を引用して述べているように、探索的因子分析の結果、単純パターンになって分析を終了するのではなく、確認的因子分析を行うことが理想的です。

探索的因子分析では、単純パターンになるよう分析を進めます。しかし、現実には全ての項目が1つの因子とだけ関連し、他の因子との因子負荷量が0とは限りません。多くの場合、どの項目も全ての因子が0より大きな因子負荷を示します。完全な単純パターンのモデルが、実際のデータにどの程度適合しているかは探索的因子分析だけでは判断できませんが、確認的因子分析を用いれば、それが可能となります。[12]

2つ目として、因子の抽出法に最尤法を用いる場合には特にですが、探索的因子分析はサンプルサイズ(回答者の人数)を十分に増やすことが必要です。その理由は、因子分析に限りませんが、推定を行う分析において、サンプルサイズが小さいと、手元のデータに過剰に適合したモデルが生成されるためです。すると、同じ質問項目を用いて再度調査を行い再び因子分析を行っても、同様の結果が再現されにくくなります。

加えて、探索的因子分析は特に、サンプルサイズが小さいと因子負荷量がうまく推定されず解が求められない不適解が生じやすくなります。不適解が生じると、分析が中断されてしまい探索的因子分析の結果を得ることができません。Fabrigar et al. (1999)[13] は、サンプルサイズは400以上を推奨しています[14]。

脚注

[1] 同じ因子分析という名前で、確認的因子分析と呼ばれる分析方法もあります。確認的因子分析は、項目群がある概念（因子）を測定しているという仮説の下でアンケートを実施し、各項目群に対して、それらの背後に因子が想定通りまとまっているかを調べるために行う因子分析です。確認的因子分析の詳細については、当社コラムをご参照ください。

[2] 平行分析以外にも最小平均偏相関（MAP）と呼ばれるものも用いられます。因子分析は、項目間の関連性に基づいて、項目間で共通して影響を与える因子を探し出すために行う分析です。その内部では「項目間の関連性は、因子による影響で生じたもの」と捉えた分析が行われます。よって、因子分析が最適に行われている時、因子の影響を取り除けば項目間の関連性はなくなるはずです。

以上のことを利用して、因子の影響を取り除いた後の項目間の相関(偏相関といいます)の平均を算出し、それが最小となる因子数を選択するのがMAPです。MAP法は、他の手法と比べて因子数を少なめに見積もる特徴があり、少ない因子数で因子を検討したいときに用いられます。

[3] 因子の持つ情報量の大きさは、厳密には固有値の大きさを表します。固有値とは、それぞれの因子が説明する分散の大きさを表します。固有値の合計は項目数の数となります。

[4] ここでいう因子間の関係性の仮定とは、「抽出した因子が相関するか否か」を指し、因子同士が相関しない仮定を直交解、相関する仮定を斜交解と呼びます。一般的に、大抵の物事は多少なりとも関連しあっていると考えられるため、探索的因子分析においては、因子と因子の間には、「少しでも関連はある」ことが前提とされ、斜交解が選択されます。後述するオブリミン回転も、斜交解である回転法の一種です。

[5] 最尤法には、質問項目から得られたデータが多変量正規分布を示すという仮定があります。その仮定の下、母集団において、因子と質問項目の関連性である因子負荷量や誤差分散がどのような値であれば、今手元にあるデータから計算された質問項目間の相関行列が得られる尤度(確率)を最大化できるかという観点から計算されます。尤度を最大にできるような因子負荷量を算出するわけです。

よって、因子負荷量は母集団における因子負荷量の推定値となります。最小二乗法と呼ばれる方法もありますが、こちらは母集団に関する前提を置いていません。相関行列の内、共通因子で説明される部分(因子負荷行列の転置×因子負荷行列)におけるモデルと実際のデータの差を最小にするような因子負荷量を算出します。データが少ないなど多変量正規性が仮定できない際に最小二乗法を使用します。

[6] オブリミン回転は、脚注6にある単純パターンの条件の3を満たすような計算をしており、各項目にかかる全因子の因子負荷量の2乗の積の和を最小にします。プロマックス回転という回転方法も有名ですが、近年では推奨されていません。

オブリミン回転では、因子負荷行列がどの程度単純構造に近いかを数学的に表現した回転基準という指標を最適化して回転後の因子負荷行列を求めます。その一方で、プロマックス回転では回転基準を最適化しているわけではないため、単純構造が得られにくいのです (山本 2019)。プロマックス回転は計算が簡便なため、古くは用いられていましたが、以上のような理由により、計算ソフトが発達した現在は用いられなくなっています。

山本　倫生 (2019). 因子分析モデルにおける因子回転問題. 計算機統計学, 32(1), 21–44.

[7] Thurstone. (1947)の定義をまとめたBrowne. (2001)の記述によると、単純パターンとは、正確には、以下の5つの条件を満たすことになります。

1. 各質問項目は少なくとも1つの因子との関連が全くない(因子負荷が0)こと
2. 各因子は少なくとも因子数分の項目に対して因子負荷が0であること。(今回は、因子数が、3なので、各因子は、最低でも3つの質問項目と因子負荷が0であるべきということです。)
3. 1つの質問項目において2つの因子に着目した場合に，1つの因子との因子負荷が0でもう一方の因子との因子負荷が0でない項目があること。
4. 因子数が4以上の時，その内2つの因子に着目した場合に，それら2つの因子との因子負荷量が0である項目があること。
5. 2つの因子に着目した場合に，どちらの因子との因子負荷量も0である項目が少ないこと

Browne, M. W. (2001). An overview of analytic rotation in exploratory factor analysis. Multivariate Behavioral Research, 36(1), 111–150.

Thurstone, L. L. (1947). Multiple-factor analysis: a development and expansion of the vectors of mind. University of Chicago Press.

[8] 分析者によっては、「複数の因子にまたがって因子負荷量が大きいが、因子負荷量は十分に高いため概念を捉えられてはいると見なせる。項目数を減らしたくない考えもあり、単純パターンまで仕上げられていないがこの項目を残す」と、複数の因子に負荷量が大きい項目でも削除しない判断をすることがあります。

[9] この妥当性は、「測定に用いた質問項目が、何らかの物事や概念を別個に測定できていると統計学的に見なせる程度」を表す因子妥当性と呼ばれます。詳しくは、当社コラムをご覧ください。

[10] Orçan, F. (2018). Exploratory and confirmatory factor analysis: Which one to use first? Journal of Measurement and Evaluation in Education and Psychology, 9(4), 414–421.

[11] Bandalos, D. L., & Finney, S. J. (2010). Factor analysis: Exploratory and confirmatory. In G. R. Hancock & R. O. Mueller (Eds.), The reviewer’s guide to quantitative methods in the social sciences (pp. 93–114). Routledge.

[12] より厳密にこの検証を行うならば、同じ質問項目を用いたサーベイを再度行い、新しいデータで確認的因子分析を行うことがもっとも望ましいです。探索的因子分析で示された因子モデルが新規のデータに対してもよくあてはまっていることを検証すれば、その因子モデルの頑健性をより正確に検証できます。

[13] Fabrigar, L. R., Wegener, D. T., MacCallum, R. C., & Strahan, E. J. (1999). Evaluating the use of exploratory factor analysis in psychological research. Psychological Methods, 4(3), 272–299.

[14] Goretzko et al. (2021) は Fabrigar et al. (1999) の基準がどの程度採用されているかを調べるため、2007年から 2017年までの間に探索的分析を使用した304の研究をレビューしました。その結果、レビュー対象の研究のうち、約50％が400以上、67％が300以上、80％が200以上のサンプルサイズを用いていると報告しました。

またGoretzko (2021) は複数のシミュレーション研究を紹介し、必要なサンプルサイズに項目数の多い少ないは無関連であることを指摘しています。さらに少ないサンプルサイズでもモデルの再現性を高めるには、各項目の共通性を大きくし、かつ1つの因子と関連する項目数を多くすることが必要であるとも述べています。共通性とは、各項目のデータの分散の内、全因子で説明される部分の大きさで、全因子からの因子負荷量の2乗和となります。

Goretzko, D., Pham, T. T. H., & Bühner, M. (2021). Exploratory factor analysis: Current use, methodological developments and recommendations for good practice. Current Psychology, 40(8), 3510–3521.

Fabrigar, L. R., Wegener, D. T., MacCallum, R. C., & Strahan, E. J. (1999). Evaluating the use of exploratory factor analysis in psychological research. Psychological Methods, 4(3), 272–299.

---

執筆者

間賀田 悠吾　株式会社ビジネスリサーチラボ アソシエイトフェロー
関西大学社会学部卒業、大阪府立大学大学院人間社会システム科学研究科博士前期課程修了、修士(学術)。自己対話における人称代名詞や文の形式の違いが動機づけやパフォーマンスにどのような影響を及ぼすかに注目し、英語話者と日本語話者を対象として文化的背景を考慮した実験研究を行っている。単純な統計解析では捉えきれない特徴を、発展的な解析方法を用いてデータから抽出することを得意としている。