様々なデータを分析して人材マネジメントの意思決定に役立てることが重要です。その中で、変数間の関係性を理解し、「何が何に影響しているのか」を把握することは、効果的な施策を立案する上で求められます。変数をその性質によって「外生変数」と「内生変数」に分類することがあります。

組織サーベイを例に考えてみましょう。「勤続年数」は何かに影響を及ぼす要因の指標（外生変数）として扱われることが多いです。一方、「職務満足」や「組織コミットメント」は、様々な要因によって影響を受ける結果にあたる指標（内生変数）と捉えることができます。このように指標の役割を整理することで、複雑な組織現象を体系的に理解できるようになります。

とりわけ「構造方程式モデリング（Structural Equation Modeling：SEM）」と呼ばれる統計手法では、外生変数と内生変数の区別が重要になります。このアプローチは、直接観測できない潜在的な概念（例えば、モチベーション、エンゲージメント）も含めて、指標間の複雑な関係性をモデル化することができます。人事データの分析においても、SEMは従業員の態度や行動の関係についての仮説を検証するために活用されています。

本コラムでは、外生変数と内生変数の定義から始め、それらが組織サーベイでどのように活用されるのか、また両者を区別する意義は何かについて説明します。エビデンスに基づいた人材マネジメントを実践するための一助となればと思います。

変数、外生変数、内生変数の定義

最初に、外生変数と内生変数に共通する「変数」から説明します。変数（variable）とは、値が変化する量のことであり、サーベイなどで捉える概念や事柄に関する回答者の特徴を表すものです。モチベーションやエンゲージメントは概念ですが、それらについてアンケートに回答を求めてデータ化すれば、個々の回答者の特徴を表す情報となり、変数となります。サーベイの実施前に考える段階では概念として取り上げていたものが、サーベイで測定しデータ化したら変数として扱われるようになると理解すれば、ひとまず問題ありません。

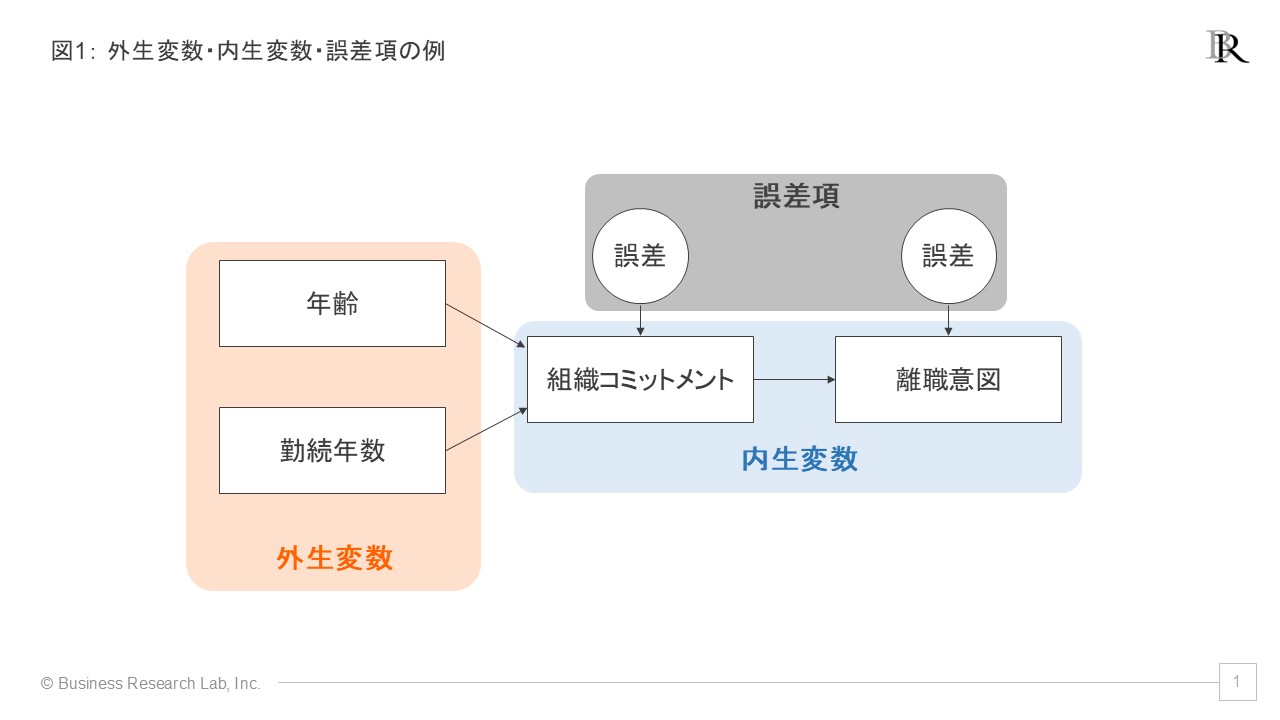
外生変数（exogenous variables）とは、モデルの中で「他の変数から影響を受けない」あるいは「モデル内部で説明されない」変数を指します。構造方程式モデリング（SEM）のパス図でいうと、外から片矢印を出すだけで、他の変数からの片矢印が刺さらない変数が外生変数となります[1]。基本的には仮説によりますが、例えば、従業員個人の「性別」「年齢」「勤続年数」などのデモグラフィック指標や、「教育プログラムの有無」「部門の違い」など、組織側の要因を外生変数として設定することが多いです。

外生変数の特徴として、少なくともモデル内では「所与のもの」として扱われることが挙げられます。その値がなぜそうなっているのかをモデル内で説明しようとはしません。例えば、従業員の「年齢」がなぜその値なのかを組織内の要因で説明することはせず、「外から与えられた条件」として扱います。そのため、外生変数はモデルの「出発点」や「起点」としての役割を果たします。

対して、内生変数（endogenous variables）とは、モデルの中で「他の変数から影響を受ける」変数のことです。パス図では、他の変数から矢印が刺さる変数が内生変数となります。これも仮説によりますが、例えば、「職務満足」「組織コミットメント」「離職意向」などが挙げられます。これらは、外生変数や他の内生変数によって「説明される」形になります。

内生変数の特徴として、モデル内で「なぜその値になるのか」を説明しようとする点があります。例えば「職務満足」という内生変数については、「勤続年数」や「職場環境」といった外生変数や、場合によっては他の内生変数からの影響を受けて程度・値が定まると考えます。それに応じて、内生変数には「誤差項」が設定され、モデルで説明されない変動部分があることを表現します[2]。

ある変数が外生変数か内生変数かは絶対的なものではなく、分析者が設定するモデルに依存することを理解しておく必要があります。例えば、ある調査では「リーダーシップスタイル」を外生変数として扱うかもしれませんが、別の調査では「組織文化」や「従業員の特性」から影響を受ける内生変数として扱うこともあります。すなわち、変数の性質というよりも、特定の分析モデルにおける役割として外生・内生を捉えるのが適切と言えるでしょう。

外生変数と内生変数の区別は推定方法にも影響します。外生変数は「独立変数」のような役割を持ち、その変動は外部から与えられるものとして扱われるため、他の変数との相関関係はあっても、モデル内でその変動が説明されることはありません。一方、内生変数は「従属変数」のような役割を持ち、その変動の一部がモデル内の他の変数によって説明されると想定します[3]。

構造方程式モデリングの概要

構造方程式モデリング（Structural Equation Modeling：SEM）は、人事領域のデータ分析でも有効な統計的手法です[4]。SEMの特徴は、直接観測できない潜在変数も含めた複雑な変数間の関係性を同時に分析できる点にあります。例えば「職務満足」「組織コミットメント」「リーダーシップの質」など、直接測定できない概念も含めた包括的なモデルを構築できるため、便利です。

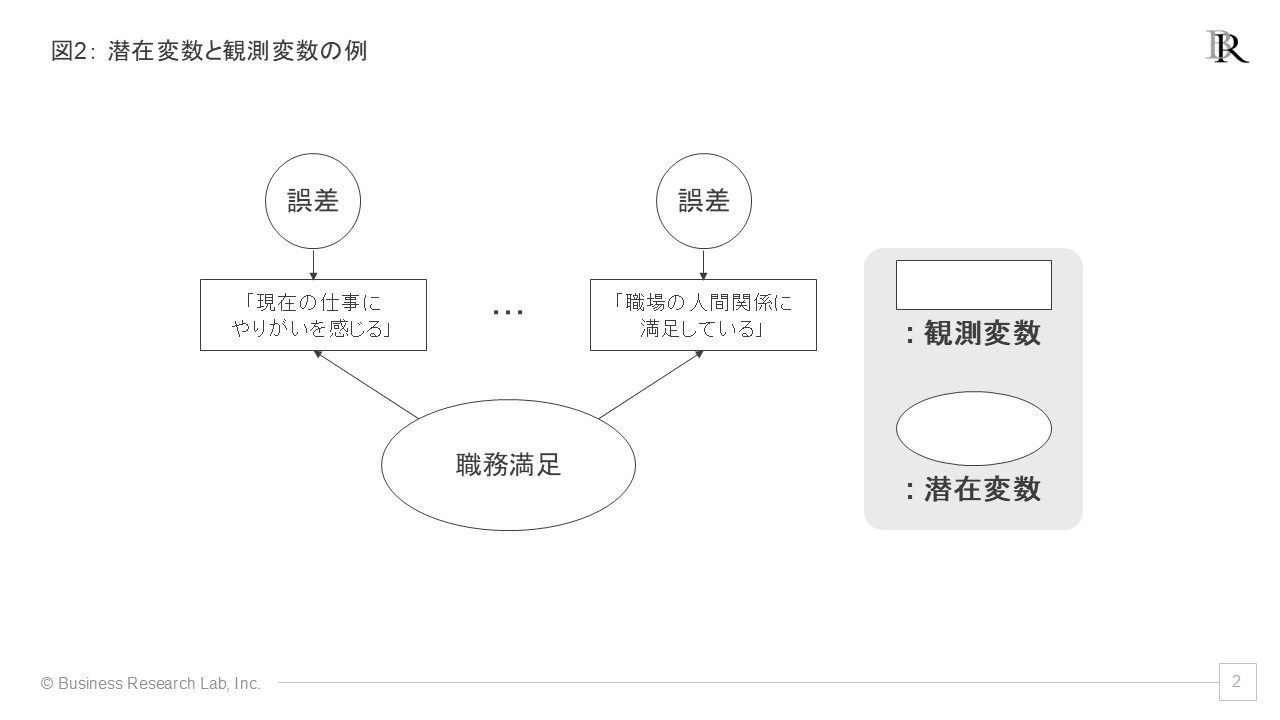
SEMは、大きく2つの部分から構成されます。まず測定モデルは、潜在変数（例えば「職務満足」という概念）を測定するための質問項目（観測変数）との関係を定義する部分です。例えば、「職務満足」という潜在変数を測定するために「現在の仕事にやりがいを感じる」「職場の人間関係に満足している」などの質問項目（観測変数）を用意し、これらの回答がどの程度「職務満足」という概念を反映しているかを評価します[5]。

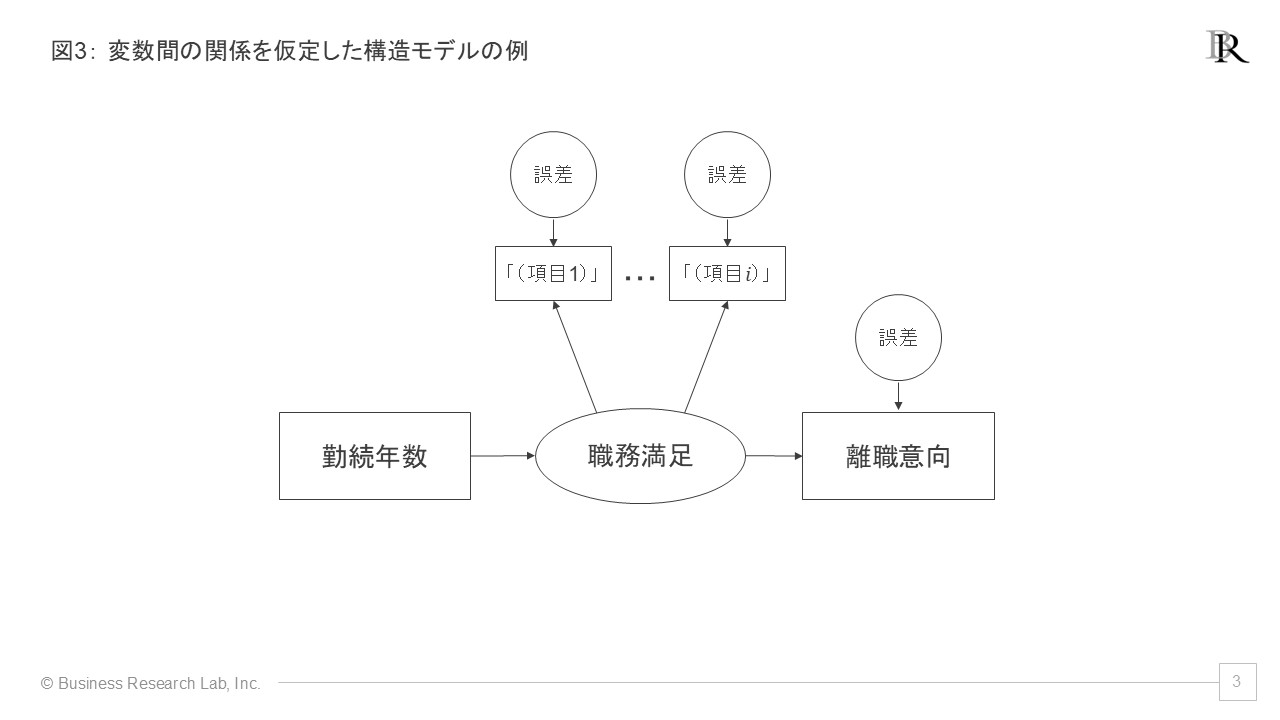
続いて構造モデルは、外生変数と内生変数、あるいは内生変数同士の関係（パス）を定義する部分です。例えば「勤続年数」（外生変数）が「職務満足」（内生変数）にどの程度影響を与え、その「職務満足」が「離職意向」（内生変数）にどの程度影響するか、といった関係性をモデル化します。SEMにおいては、「測定モデルでうまく心理・行動概念を測定できているか」を確認しつつ、「構造モデルで想定されるパス（経路）を仮定し、データとの適合度がどの程度良いか」を評価します。

SEMを実施する際のステップとしては、研究知や実践知に基づいて仮説モデルを構築します。この段階で、どの変数を外生変数とし、どの変数を内生変数とするか、またそれらの間にどのような関係性（パス）を仮定するかを決定します。その上で、実際のデータをモデルに当てはめ、パラメータの推定を行います。そして、モデルの適合度を評価し、必要に応じてモデルの修正を検討します[6]。

SEMの利点の一つは、直接効果と間接効果を区別できることです。例えば、「リーダーシップスタイル」（外生変数）が「職場の雰囲気」（内生変数）を通じて「従業員のパフォーマンス」（内生変数）に間接的に影響する、といった複雑な関係性も分析できます。これによって、「なぜ」「どのように」というメカニズムに関する理解が深まります。

しかし、注意点もあります。SEMの構造モデルのパスは、しばしば「原因→結果」の流れを表す矢印で描かれますが、パス図を描いてパラメータを推定しただけで因果関係がただちに保証されるわけではありません[7]。特に組織サーベイの場合、多くは横断的なデータをもとにモデル化されることが多いので、「○○が原因で△△になる」と確定的に言えるわけではなく、「仮にこういう方向の影響があると仮定して分析した場合、この仮定に基づくモデルはデータとどの程度整合するか」を評価すると理解すると良いでしょう。

組織サーベイにおける例

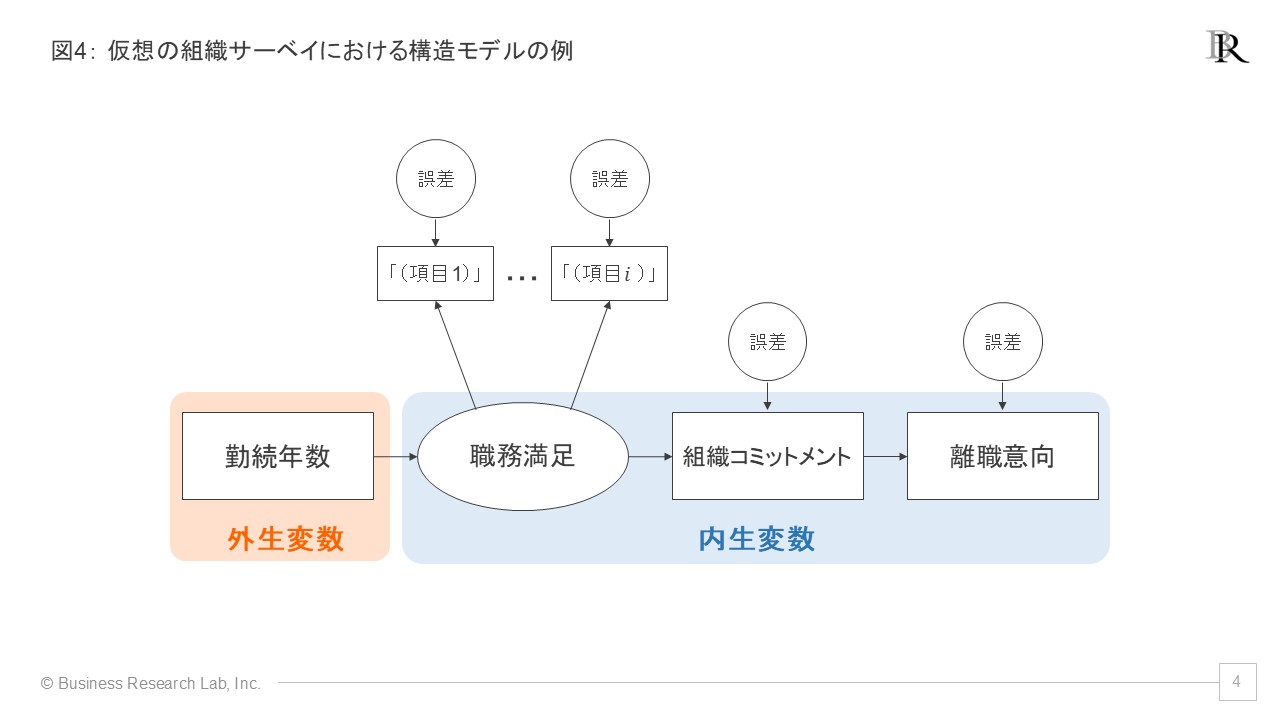
ある企業の組織サーベイを想定し、外生変数と内生変数の活用例を見ていきましょう。この企業では従業員の離職率が課題となっており、「何が従業員の離職意向に影響しているのか」を構造方程式モデリング（SEM）によって分析しようとしています。

分析に用いる変数として、外生変数と内生変数を次のように設定します。外生変数としては、従業員属性（例：性別、年齢、勤続年数、学歴など）や組織要因（例：研修プログラムの実施状況、部門間の構造的特徴など）が考えられます。これらは、モデル内で他の変数によって説明されるのではなく、「与えられた条件」として扱われます。

一方、内生変数としては、職務満足（職場環境に対する従業員の満足度）、組織コミットメント（会社にどれほど愛着・帰属意識を持っているか）、離職意向（従業員がどの程度退職を考えているか）などが挙げられます。これらは、外生変数や他の内生変数から影響を受ける形でモデル化されます。

変数の測定方法としては、従業員属性は人事データベースから抽出し、職務満足や組織コミットメント、離職意向については、アンケートの複数の質問項目から測定します。例えば、職務満足は「現在の仕事内容に満足している」「職場の人間関係に満足している」「待遇に満足している」などの複数項目の回答から構成される潜在変数として扱います。

仮説モデルの一例として、次のような因果関係を想定してみましょう。

• 「勤続年数（外生変数）」が高いほど、職務満足（内生変数）が高いという仮説が考えられます。これは、長く勤めることで仕事への理解が深まり、より効率的に業務を進められるようになることで満足度が高まる可能性を示しています。
• 「職務満足（内生変数）」が高いほど、組織コミットメント（内生変数）も高いという仮説が立てられます。仕事に満足している従業員は、組織への愛着も高まりやすいと考えられるためです。
• 「組織コミットメント（内生変数）」が高いほど、離職意向（内生変数）が低いという仮説も考えられます。組織に強い帰属意識を持つ従業員は、転職を考える可能性が低いと想定されるからです。

このとき、SEMのパス図として「勤続年数→職務満足→組織コミットメント→離職意向」という矢印を描き、関連が表現されます。「勤続年数」は他の変数からは説明されない外生的な要因、「職務満足」「組織コミットメント」「離職意向」はそれぞれ他の要因から説明され得る内生的な変数という位置づけになります。

このモデルをデータに当てはめると、各パス（矢印）の強さ（標準化係数）や統計的有意性が算出されます。例えば、「勤続年数→職務満足」のパス係数が0.25で有意であれば、勤続年数が1標準偏差大きいと、職務満足は0.25標準偏差大きいと解釈できます。同様に「職務満足→組織コミットメント」のパス係数が0.50で有意であれば、職務満足が1標準偏差大きいと、組織コミットメントは0.5標準偏差大きいと解釈できます。

例えば、分析結果から「職務満足」と「組織コミットメント」の向上が離職意向の低減に重要だとわかれば、それらを高めるための施策（例えば、職場環境の改善、キャリア支援、評価制度の改定など）を優先的に検討することができます。勤続年数の短い従業員の満足度が特に低いことが判明すれば、新入社員や中途採用者向けのオンボーディングの強化などにつなげることができます。

外生変数と内生変数を区別する意義

外生変数と内生変数を区別することには、データ分析と実務応用の両面で意義があります。この区別によって、「何が原因で何が結果か」という仮説について、概念的な整理がしやすくなります。例えば「性別」「年齢」などの特性は組織内で変化するものではないため外生変数として位置づけ、「満足度」や「モチベーション」は影響を受ける内生変数として区別することで、分析の枠組みが明確になります。

この区別はモデルの解釈をシンプルにします。SEMのパス図で「研修プログラム（外生変数）→スキル向上（内生変数）→業績向上（内生変数）」という矢印の流れを描くことで、変数間の関係性が理解しやすくなります。これによって、「何がどのような経路で関連するのか」という説明がしやすくなります。

実務上のメリットは、介入ポイントの明確化です。例えば、外生変数は「介入可能な要因」、内生変数は「期待される成果」として位置づけられます。人事施策を立案する際、「職場環境（外生変数）」の改善が「職務満足（内生変数）」を高め、最終的に「離職率低下（内生変数）」につながるという関連を予測できるようになります。これは「どこに働きかければ効果的か」という施策の優先順位付けに役立ちます。

ただし、SEMでモデルを描いても、それだけで因果関係が証明されるわけではないことにはやはり注意が必要です。

押さえておくべきポイント

外生変数と内生変数に関して、人事データ分析を行う上で押さえておくべきポイントをまとめます。

第一に、「外生変数」と「内生変数」は、あくまでSEMにおける構造上の役割の違いであることです。外生変数は他の変数に説明されないものであり、内生変数は他変数によって変動が説明されるものですが、この区別は絶対的なものではありません。あくまで分析者が設定したモデル上の役割に過ぎず、分析の目的やモデル設計によって位置づけが変わることもあります。

第二に、SEMでパス図を描いても、それだけで因果関係が証明されるわけではないという点です。あくまでも仮定されたモデルに基づき、データとどの程度整合があるかを見るのがSEMの役割です。「AがBに影響している」というモデルと「BがAに影響している」という逆方向のモデルが同じくらい適合することもあります。

第三に、分析結果の解釈は慎重に行うべきです。「統計的に有意」であっても、効果量の大きさや実際の現場の状況を併せて検討することが大切です。パス係数が有意でも、その大きさが実務的にみて重要な意味を持つかどうかは別問題です。

第四に、サンプルサイズと推定の安定性にも注意が必要です。SEMは比較的大きなサンプルサイズを必要とする手法であり、特に複雑なモデルでは十分なデータ数がないと推定結果が不安定になります。SEMの解析には、最低でも100-150名のサンプルサイズが必要とされ[8]、実証研究ではそれ以上のサンプルサイズが求められます。

第五に、SEMの結果だけでなく、質的データや現場の知見と組み合わせた総合的な解釈が求められます。統計モデルはあくまで一つの情報であり、全ての要因や関係性を完全に捉えることはできません。他の情報源（例えば、インタビューや現場観察など）からの知見と組み合わせて解釈することで、より深い組織理解につながります。

脚注

[1] SEMのパス図では、変数間の相関関係を表す両矢印を描くこともあります。例えば、外生変数間に相関を仮定する場合、それらの変数間に両矢印を描くことで、それを表現します。外生変数は「パス（片矢印）が刺さっていない変数」なため、相関を表す両矢印が刺さっていても、パスが刺さっていないならば外生変数として扱われます。

[2] 内生変数に誤差項が設定されるのは、モデル内の変数が完全には他の変数で説明されないためです。すなわち、モデルに含まれていない変数や測定誤差、ランダムな要素による影響を扱う必要があります。誤差項は、このような説明されない変動を統計的に表現し、モデルの推定を現実的かつ妥当なものにしています。

なお、一般的に、SEMにおいて外生変数自体には誤差項を設定しません。外生変数はモデルの中で「外部から与えられ、モデル内では説明されない変数」として扱われるためです。誤差項は「モデル内で説明されない残余部分」を示すものであるため、最初から説明されない前提である外生変数には、論理的に誤差項を設定する必要がありません。ただし、外生変数が潜在変数として定義される場合、その潜在変数を測定する指標（観測変数）には測定誤差が存在します。この測定誤差を表す誤差項は指標に対して設定されますが、外生変数にあたる潜在変数そのものには構造モデル上の予測誤差項は設けられません。

[3] 外生変数と内生変数は、「独立変数」「従属変数」と呼ばれることもありますが、SEMの文脈では、この用語が必ずしも因果的な独立性や従属性を保証しません。潜在変数を扱う場合、内生変数が他の内生変数を予測する役割を持つこともあります。

[4] 構造方程式モデリングの詳細は当社コラムやセミナーレポートをご覧ください。

[5] 複数の質問項目の回答データから特定の概念の得点を捉える場合、ここにあるようにSEMで潜在変数として取り上げる方法のほかに、一般によく用いられる方法として、回答データの平均値や合計値を取ってその概念の得点とする方法があります。ここの例でいえば、回答者ごとに職務満足の質問項目への回答データの平均や合計をとり、その値を各回答者の職務満足得点とするやり方です。この得点化の場合、職務満足得点は平均値や合計値によって「観測された得点となった」と扱うため、平均や合計で実際にデータ化したこの得点は観測変数として扱われます。

[6] 識別問題とは、SEMにおいて推定すべきパラメータが一意に決定できるかという問題です。モデルが識別されていない場合、複数の異なるパラメータ値が同じ適合度を示すため、信頼性のある結果が得られません。識別には、モデルの自由度が0以上である、潜在変数にスケールが設定されている、再帰的モデルである（変数間に双方向の因果関係がない）などの条件が必要です。

[7] 組織サーベイでは、横断的なデータを用いて分析されることがあるため、変数間の時系列的な順序を確認できません。このため、「職務満足度が組織コミットメントを高める」のか、逆に「コミットメントが高いため職務満足度が高い」のか、明確に区別できないことがあります。また、未観測の共通原因（交絡因子）が存在すると見かけ上の関係が生じる可能性があるため、結果の解釈には注意が必要です。

[8] Schumacker, R. E., & Lomax, R. G. (2010). A beginner’s guide to structural equation modeling (3rd ed.). Routledge/Taylor & Francis Group.

執筆者

伊達 洋駆　株式会社ビジネスリサーチラボ 代表取締役
神戸大学大学院経営学研究科 博士前期課程修了。修士（経営学）。2009年にLLPビジネスリサーチラボ、2011年に株式会社ビジネスリサーチラボを創業。以降、組織・人事領域を中心に、民間企業を対象にした調査・コンサルティング事業を展開。研究知と実践知の両方を活用した「アカデミックリサーチ」をコンセプトに、組織サーベイや人事データ分析のサービスを提供している。著書に『60分でわかる！心理的安全性 超入門』（技術評論社）や『現場でよくある課題への処方箋 人と組織の行動科学』（すばる舎）、『越境学習入門 組織を強くする「冒険人材」の育て方』（共著；日本能率協会マネジメントセンター）などがある。2022年に「日本の人事部 HRアワード2022」書籍部門 最優秀賞を受賞。東京大学大学院情報学環 特任研究員を兼務。