人事評価やアセスメント、組織サーベイなど、企業内で実施されるさまざまな測定・評価において、より精緻な分析手法はないものでしょうか。従来の古典的テスト理論では、合計点や平均値に基づく分析が主流でしたが、これには「どの質問も同じ重みづけで得点が計算される」「回答者の能力と質問の難しさを分離して考えられない」といった限界がありました。

項目反応理論は、こうした限界を克服し、テストや質問紙における「項目（質問）」と「回答者」の特性を分離して分析できるアプローチです。人事領域においては、採用試験、能力テスト、組織サーベイなどのデータをより深く理解するために、この理論の活用があり得ます。

項目反応理論の核心となる考え方は、「回答者の能力や態度」と「質問項目の特性」を数理モデルによって切り分けて表現することにあります。本コラムでは、この理論の中でも「困難度」というパラメータに焦点を当て、人事領域にどのように活用できるかを解説します。

項目反応理論とは

項目反応理論は、テストやアンケートなどで得られるデータを回答者と項目（質問）の特徴に分けた観点で分析するときに用いられる統計モデルの総称です。項目反応理論の基本的な考え方は、「回答者が持つ潜在的特性（潜在能力や態度、意識など）と、各項目の特性（困難度や識別力など）が回答パターンに影響を与えている」というものです。

例えば学力テストであれば、回答者の「能力（例えば数学の実力）」と問題（項目）の「難しさ」「区別のしやすさ」などが組み合わさって、回答が正答になるかどうかが決まる、と考えます。リッカート尺度のアンケートであれば、回答者の「ある意識や態度の強さ」と質問項目における各選択肢の「選ばれやすさ」を組み合わせることで、回答結果（「当てはまる」「当てはまらない」「どちらともいえない」など）が生まれる、とみなします。

困難度とは

困難度の直感的な意味を考えてみましょう。「困難度」という言葉を聞くと、多くの方は「問題がどれだけ解きにくいか」「どれだけ難しいか」をイメージすると思います。項目反応理論でも基本的には同様で、困難度パラメータは「一定の潜在特性の水準において、回答者がその項目を肯定（または正答）する確率が50%になるポイント」がどのあたりに位置するのかを表します。

学力テストの場合なら、「能力がどのくらい高い人だったら半分くらいの確率で正解できるか」を指します。アンケートの場合は、例えば「意識や態度がどのくらい強い人なら、『はい/いいえのうち、はいを選ぶ』確率が50%を超えるか」のように考えられます。

項目反応理論モデルでは、「困難度パラメータ」をbと表記します。困難度パラメータは通常、潜在特性尺度に合わせて設定されます。一般に潜在特性の尺度は平均0、標準偏差1の標準正規分布を仮定し、例えば困難度b=1.0の項目は、潜在特性が平均より1標準偏差高い回答者が50%の確率で正答できる難しさを持つ、ということになります。

このように困難度パラメータは、「項目の難しさ」を定量的に表現する方法として、テスト開発やアンケート分析において重要な情報を提供してくれます。

項目反応理論モデルと困難度パラメータ

項目反応理論で頻繁に用いられる数理モデルである「2パラメータ・ロジスティックモデル（2PL）」を中心に、困難度パラメータがどのようにモデル化されるかを見ていきましょう。これは、正解/不正解やはい/いいえ、参加/不参加、チェックボックスへのチェックの有無のように、2つの値しかとらないデータに対して用いられるモデルです。このようなデータは、正解・はい・参加・チェックありなどを1、もう一方を0と入力する01データとして扱うことが多いです[1]。

2パラメータロジスティックモデル（2PL）では、ある回答者の潜在特性θ（シータ）と、ある項目iの識別力a_i・困難度b_iを用いて、回答が正答（または肯定）となる確率P(X_i=1|θ)を[2]下記のようにモデル化します[3]。

この数式で使われている記号の意味は次の通りです[4]。

• θ：回答者の潜在特性の値（例えば能力や態度の強さを数値化したもの）
• a_i：識別力パラメータ（項目が回答者の潜在特性をどれほど識別できるか）
• b_i：困難度パラメータ（どの程度の潜在特性があれば半分程度の確率でその項目を肯定するか）
• X_i：項目iへの回答が「正答（肯定）」なら1、「誤答（否定）」なら0

この数式において、θ-b_iという部分に注目してください。これは「回答者の潜在特性と項目の困難度の差」を表しています。

• θ-b_iが大きい（すなわち潜在特性θが困難度b_iより高い）ほど、exp{-a_i(θ-b_i)}は小さくなります。すると分母が小さくなるので、全体として確率が高くなります（項目を肯定しやすくなります）。
• 反対に、θ-b_iが小さい（すなわち潜在特性θが困難度b_iより低い）ほど、exp{-a_i(θ-b_i)}は大きくなります。すると分母が大きくなるので、全体として確率が低くなります（項目を肯定しにくくなります）。
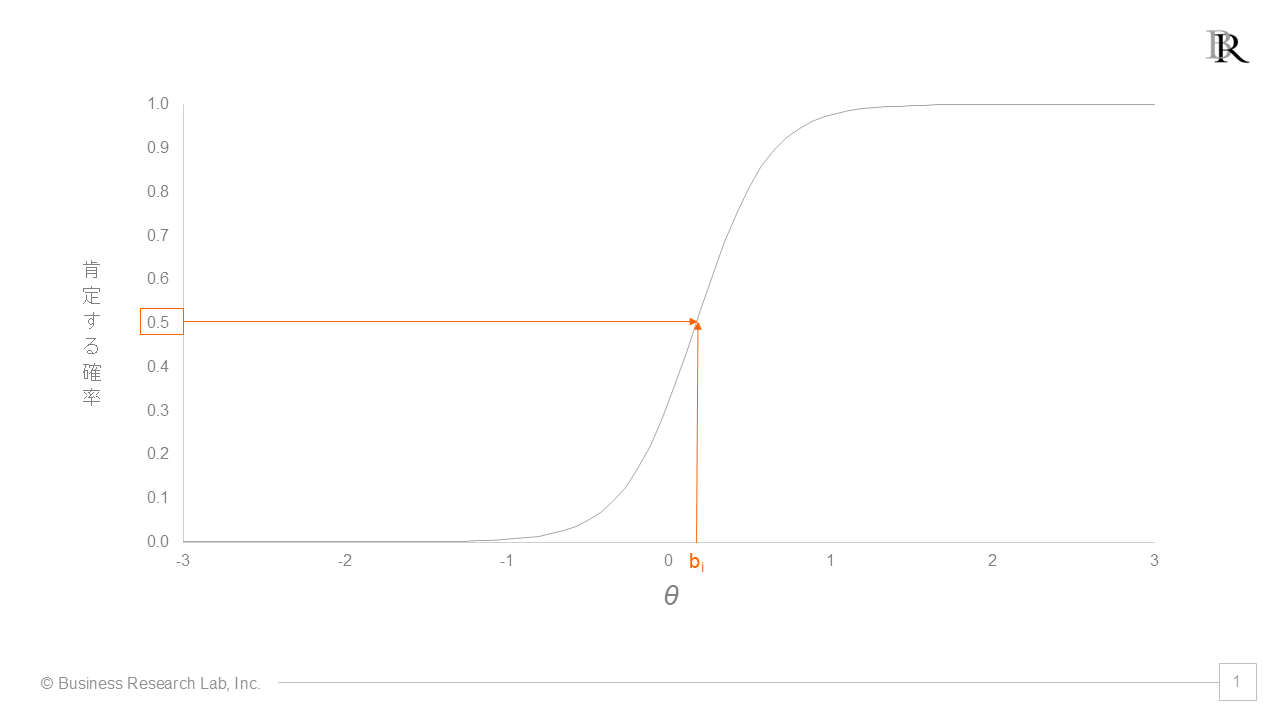
• θ=b_iのとき、θ-b_i=0なので、exp{-a_i(0)}=1となります。よって確率は1/(1+1)=0.5つまり50%になります。これは「潜在特性θがちょうど困難度b_iの値に等しいとき、その項目を肯定する確率は50%になる」ということであり、これがまさに困難度パラメータの定義です。

識別力パラメータa_iは、この確率曲線の傾きを決定します[5]。a_iが大きいほど、曲線は急峻になり、潜在特性の値の前後で正答確率が急激に変化します。その潜在特性の程度を超えているか否かによって肯定/否定がはっきり分かれる状態であり、その項目における潜在特性を識別する能力が高いといえます。

この2PLモデルを図示すると、S字型の曲線（項目特性曲線）が得られます。この曲線上で、正答確率が0.5となる点の横軸の値が、困難度パラメータb_iに対応します。

組織サーベイの例

人事領域における項目反応理論の活用例として、組織サーベイを取り上げてみましょう。組織サーベイでは、企業などで従業員のエンゲージメントを測るために、例えば次のような項目を複数個含む設問を5件法などで回答してもらうアンケートを実施することがあります。

「私は会社の方針に共感している」

1. 全くそう思わない
2. あまりそう思わない
3. どちらとも言えない
4. ややそう思う
5. 非常にそう思う

組織サーベイでは、いくつかの質問を用意し、その合計スコアや平均スコアを指標とすることも多いのですが、項目反応理論を使うと、例えば、各質問（項目）ごとに「回答者の『エンゲージメントの高さ』によって、回答がどう変化するか」をモデル化することができます。

リッカート尺度のような多段階評価の場合、正誤二値ではないため、例えば、段階反応モデルなどを用いることになります。段階反応モデルでは、それぞれのカテゴリ（例：1〜5段階）ごとに、「閾値」と呼ばれるパラメータが設定されます。

各閾値パラメータb_{i,k}は、潜在特性θにおいて、カテゴリkとカテゴリk+1を選ぶ確率がちょうど等しくなるポイントとして定義されます。

• b_{i,1}：「1」から「2」へ回答がシフトする閾値
• b_{i,2}：「2」から「3」へ回答がシフトする閾値
• b_{i,3}：「3」から「4」へ回答がシフトする閾値
• b_{i,4}：「4」から「5」へ回答がシフトする閾値

学力テストにおける「正答・誤答」モデルが50%を基準に正答・誤答が切り替わるタイミングを検討したのと同じように、「潜在特性の水準がどこにあると、ある選択肢を選ぶ確率がその前の選択肢を選ぶ確率を超えて、選択が切り替わるのか」を検討する考え方です。このように、複数のカテゴリがある場合、それぞれの境界ごとに「困難度に相当するパラメータ」が設定されるというイメージを持つとわかりやすいでしょう。

段階反応モデルは次のような式で表すことができます。カテゴリk以上の回答を選択する確率を次のようにモデル化します[6]。

ちょうどカテゴリkを選ぶ確率は、次のように計算することができます。

P(X_i=k|θ)=P^*(X_i≥k|θ)-P^*(X_i≥k+1|θ)

これは「カテゴリk以上を選ぶ確率」から「カテゴリk+1以上を選ぶ確率」を引くことで、「ちょうどカテゴリkを選ぶ確率」を算出するという考え方です[7]。

具体的なイメージとして、先ほどの「私は会社の方針に共感している」という設問について考えてみましょう。

潜在特性「エンゲージメント度合い」をθで表すとします（例えばθが大きいほど会社への愛着が強いとします）。この項目（設問）には4つの閾値パラメータb_{i,1}, b_{i,2}, b_{i,3}, b_{i,4}が推定されます。

θが最も小さい人（エンゲージメント度合いが低い人）は、「1. 全くそう思わない」を選ぶ確率が高くなります[8]。θが一定の値（b_{i,1}）を超えると、回答が「1」から「2」にシフトしやすくなります。さらにθがb_{i,2}を超えると、今度は「2」から「3」を選ぶ確率が高くなります[9]。このように、潜在特性値が高くなるにつれて徐々にカテゴリが変わっていき、θが十分に大きくなると「5. 非常にそう思う」を選択する確率が上がるということです。

したがって、この各閾値b_{i,j}が大きいほど「高いエンゲージメントがないと、上位の回答（やや同意〜非常に同意）には行きにくい項目」という解釈ができます。逆に、閾値が低い項目は、「比較的エンゲージメントが低めの人でも上位の回答を選びやすい項目」とも言えます。

組織サーベイを分析する際、こうした閾値パラメータの違いに注目すると、次のような知見が得られます。例えば、次の2つの質問項目があるとします。

• 項目A：「私は会社の将来に期待している」
• 項目B：「私は自分の仕事にやりがいを感じている」

項目反応理論による分析の結果、項目Aの閾値パラメータ（特にb_{i,4}「4→5」の閾値）が非常に高く、項目Bの閾値パラメータが比較的低いことがわかったとします。

これは「会社の将来に期待する」という項目は、よほどエンゲージメントが高くないと「非常にそう思う」と回答されにくいことを示唆しています。一方で「仕事のやりがい」については、比較的エンゲージメントが低めの従業員でも「ややそう思う」「非常にそう思う」と回答しやすい項目だと解釈できます。

このような分析は、単純な平均値だけでは見えてこない、質問項目の「質」や「特性」を明らかにしてくれます。例えば平均値が同じ3.8の2つの質問項目があったとしても、その困難度パラメータが大きく異なれば、その解釈も変わってくるでしょう。

脚注

[1] この数値割り当ては、統計的にそうする必然性があるわけでなく、解釈しやすさや指標の意味付けのしやすさによりこのように設定されることが多いといえます。例えば、01データを分析する際は「0が1になったとき、他指標はどうなるか」を数理的に検証することが多く、正解やはいを1とすると、「正解する場合」や「はいと回答する場合」などが検証されて意味付けがしやすくなります。また、01データの平均を取ると正解割合やはいと答えた割合の値となり、解釈しやすい情報が得られます。

[2] P(X_i=1|θ)という表記は、「回答者が特定の潜在特性値θを持っているという条件のもとで、項目iに対して回答が『正答（あるいは肯定）』という結果（X_i=1）になる確率」を意味しています。この記号にある「|θ」は「θが与えられたもとで」という条件付きの状況を示しています。潜在特性がわかっている（または推定されている）という仮定のもとで、特定の回答行動がどのくらい起こりやすいかをモデル化するために、条件付き確率という形をとっています。

[3] この式で1を分子に置き、それを分母の式で割っているのは、項目への肯定（あるいは正答）の確率を0から1までの範囲内で表すためです。これはロジスティック関数と呼ばれ、回答者の潜在特性が項目の特性（困難度）より大きくなるほど確率が1（100%）に近づき、小さくなるほど0（0%）に近づくという性質を持っています。

[4] ここにおける「exp」とは指数関数を表す記号で、自然対数の底（約2.718）を特定の数値で累乗した値を示します。指数関数は、連続的で滑らかなS字型の曲線（ロジスティック曲線）を作り出し、回答者の潜在特性と項目の難易度との関係を確率的に表現するため、項目反応理論の数理モデルで利用されます。

[5] 識別力の詳細な解説は、当社コラムをご確認ください。

[6] P^*(X_i≥k|θ)は、「回答者の潜在特性（能力や態度など）が特定の値（θ）であるときに、その回答者が項目iに対して『カテゴリk以上』の選択肢を選ぶ確率」を意味しています。段階反応モデルは項目への回答が複数の順序付けられたカテゴリからなる場合に用いられ、例えばリッカート尺度のように、カテゴリが「まったくそう思わない」から「非常にそう思う」まで順序付けされているケースを想定しています。要するにP^*(X_i≥k|θ)は、「カテゴリkより低いものは選ばず、カテゴリk以上のどれかを選ぶ累積的な確率」を示しているのです。

[7] P^*とPには違いがあります。P^*は、あるカテゴリk以上が選ばれる累積確率を指し、ロジスティック関数を用いて定義されます。一方、Pは、その累積確率の差分として算出される、ちょうどカテゴリkが選ばれる確率を表しています。要するに、P^*が累積的な確率を意味するのに対し、Pは各カテゴリの発生確率を個別に表現したものです。

[8] θが最も小さい人が全員必ずカテゴリ1を選ぶのではないかと思った人もいるかもしれません。段階反応モデルは、あくまで「確率的な」モデルであるため、潜在特性θが非常に低い場合でも、絶対に全員が最低カテゴリを選ぶとは限りません。あくまで「カテゴリ1を選ぶ確率が最も高くなる」というだけであり、小さいながらも上位のカテゴリを選ぶ可能性は常に存在しています。これは、実際の回答者が項目に回答する際には、様々な要因や個人差、偶然の要素が関与しているため、潜在特性が低くても必ず最下位カテゴリを選ぶという「完全決定論的」なモデルではなく、「確率論的」な考え方を採用しているからです。

[9] ここでのb_{i,2}は、前出のb^*_{i,k}とは異なることに注意が必要です。前者は、「カテゴリ2よりも3を選ぶ確率が高くなり始める」潜在特性（θ）の値を指しています。他方、後者は「カテゴリ3”以上”の回答を選ぶ確率がちょうど50%になる」潜在特性（θ）の値を指しています。すなわち、θがこのb^*_{i,2}を超えた時点ではじめて、「3以上（つまりカテゴリ3～5）の回答を選択する確率」が50％を超えるという意味です。

執筆者

伊達 洋駆　株式会社ビジネスリサーチラボ 代表取締役
神戸大学大学院経営学研究科 博士前期課程修了。修士（経営学）。2009年にLLPビジネスリサーチラボ、2011年に株式会社ビジネスリサーチラボを創業。以降、組織・人事領域を中心に、民間企業を対象にした調査・コンサルティング事業を展開。研究知と実践知の両方を活用した「アカデミックリサーチ」をコンセプトに、組織サーベイや人事データ分析のサービスを提供している。著書に『60分でわかる！心理的安全性 超入門』（技術評論社）や『現場でよくある課題への処方箋 人と組織の行動科学』（すばる舎）、『越境学習入門 組織を強くする「冒険人材」の育て方』（共著；日本能率協会マネジメントセンター）などがある。2022年に「日本の人事部 HRアワード2022」書籍部門 最優秀賞を受賞。東京大学大学院情報学環 特任研究員を兼務。