本コラムでは、標準偏差と標準誤差について、組織サーベイのデータを例に用いながら解説します。企業においてエンゲージメントを測定する際、平均値を見るだけでは十分ではありません。データのばらつきを理解することが、より正確な意思決定につながります。

例えば、エンゲージメントに関する複数の質問項目に対して、5段階評価（1: 全く当てはまらない ～ 5: 非常に当てはまる）で回答を得たとします。部署Aと部署Bで同じ平均値3.5が得られたとしても、部署Aでは多くの従業員が3や4と回答し、部署Bでは1と5の両極端な回答が多かったという可能性があります。このような違いを数値で表現するのが標準偏差です。

対して、全社員の中から100名にアンケートを実施した場合、その結果がどの程度全社員の平均を反映しているのかを示す指標が必要になります。これが標準誤差です。標準誤差は、私たちが得た調査結果がどの程度信頼できるものなのかを教えてくれます。

標準偏差とは

標準偏差はデータのばらつきの大きさを示す統計量です。母集団の標準偏差は、データ全体のばらつきを表す理論的な値であり、σで表されます。一方、標本の標準偏差は、実際に測定したデータから計算される値で、sで表されます。

母集団の標準偏差については、基本的に真の値を知ることができません。そのため、標本から得られた標準偏差sを用いて母集団の標準偏差σを推定することになります。その推定値はs’と表記され、推定精度は標本サイズが大きいほど向上します。

次に、標本の標準偏差の算出方法を見ていきましょう。まず、全てのデータの平均値を計算します。次に、各データと平均値との差（偏差）を求めます。この偏差を2乗し、その合計を取ります。2乗する理由は、正の偏差と負の偏差が相殺されることを防ぐためです。この2乗和をデータ数で割った値に平方根をつけた値が、標本の標準偏差sです。

標本の標準偏差から母集団の標準偏差σを推定するには、標本の標準偏差において、2乗和をデータ数で割っていたところを、データ数から1を引いた値で割って平方根を取ります。つまり、2乗和をデータ数で割って平方根を取ると標本そのものの標準偏差sとなり、データ数から1引いた値で割って平方根を取ると母集団の標準偏差σの推定値s’になります。

データ数から1を引く理由は、より正確な推定を行うためです。例えば、5人の従業員の平均身長が170cmだと分かっているとき、4人の身長が分かれば、残り1人の身長は自動的に決まってしまいます[1]。このように、平均値が決まっているときに、本当に「自由に変えられる」データの数は、全体の数から1を引いた数になります。これを「自由度」と呼び、より正確な計算のために使用します。これによって偏りのない（バイアスのない）推定が可能になります[2]。自由度の損失を補正するために、分母にn-1を用います。

母集団の標準偏差の推定値を数式で表現すると、次のようになります。

s’=√(Σ(xi-x)²/(n-1))

ここにおいて、s’は母集団の標準偏差の推定値、xiは標準偏差を求めている指標の各データの値、xはデータの平均値、nはデータ数、Σは総和を表す記号を意味しています。例えば、5名の従業員から得られた「仕事のやりがい」の回答が3, 4, 3, 5, 5だった場合を考えてみましょう。

• 平均値の計算：(3+4+3+5+5)÷5=4
• 各データと平均値の差の2乗：(3-4)²=1　(4-4)²=0　(3-4)²=1　(5-4)²=1　(5-4)²=1
• 2乗の合計：1+0+1+1+1= 4
• (n-1)で割る：4÷(5-1)=1
• 平方根を取る：√1=1

したがって、この例での標準偏差は1となります。

なお、データが正規分布に従う場合、平均値±1標準偏差の範囲には、約68%のデータが含まれます。これは、正規分布の性質から導かれる特徴です。組織サーベイのスコアが正規分布に従うと仮定すると、平均値が4で標準偏差が1の場合、約68%の従業員の回答が3から5の範囲に収まることを意味します[3]。

標準誤差とは

標準誤差は、母平均（真の値）に対して標本平均がどの程度ばらついているかを表しています。

全社員の真の平均エンゲージメントスコアを知りたい場合、全員にアンケートを取ることが理想的ですが、現実的には一部の従業員から回答を得ることになります。標準誤差は、この一部のデータから計算した平均値が、全体の真の平均値をどの程度正確に推定できているかを示します。

標準誤差の計算式は次の通りです。

SE=s’/√n

ここにおいて、SEは標準誤差、s’は母集団標準偏差の推定値、nはサンプルサイズを意味します。

この式は、中心極限定理に基づいています。中心極限定理とは、標本平均の分布が、サンプルサイズが大きくなるにつれて正規分布に近づくという定理です。母集団がどのような分布に従っていても、そこから無作為に抽出した標本の平均値の分布は、サンプルサイズが十分大きければ、正規分布に従うということです[4]。

この性質によって、標本平均の分布は正規分布で近似でき、その標準偏差が標準誤差となります。要するに、標準誤差は「もし同じサイズの標本を何度も抽出したとき、それぞれの標本平均がどの程度ばらつくか」を表現しています。理論的には、母集団から同じサイズ（n）の標本を無限回抽出し、それぞれの標本平均を計算したとき、それらの標本平均の標準偏差が標準誤差に一致します。

例えば、標本標準偏差が1.0で、サンプルサイズが100の場合を考えてみましょう。

SE=1.0/√100=1.0/10=0.1

この場合、「もし同じ調査を何度も実施したとすれば、得られる標本平均は母平均の±0.1の範囲に、約68%の確率で収まる」ということを意味します。これは正規分布の性質から導かれます。同様に、母平均の±2SEの範囲には約95%の確率で、±3SEの範囲には約99.7%の確率で標本平均が収まることになります。

標準誤差はサンプルサイズの平方根に反比例します。例えば、サンプルサイズを4倍（100人から400人）にした場合、次のようになります。

• 元の標準誤差：SE₁=s/√100=s/10
• 新しい標準誤差：SE₂=s/√400=s/20

したがって、SE₂=SE₁/2となります。これは、サンプルサイズを4倍にすると標準誤差が半分になることを指しています。一般的に、標準誤差をx分の1にするためには、サンプルサイズをx²倍にする必要があります。例えば、標準誤差を3分の1にしたい場合、サンプルサイズを9倍にする必要があります。この性質は、必要なサンプルサイズを決定する際の指針の一つとなります。

標準偏差と標準誤差の違い

標準偏差と標準誤差は、どちらもデータのばらつきを表す指標という点で共通しています。しかし、そのばらつきの対象と解釈は異なります。この違いを理解することは、データ分析において適切な指標を選択し、正しい解釈を行うために重要です。

標準偏差は、個々の観測値（従業員の回答）のばらつきを表します。これは、データの散らばり具合を直接的に表しています。エンゲージメントスコアの標準偏差が大きいということは、従業員間で回答にばらつきがあることを意味します。例えば、ある部署で平均値は4.0だが標準偏差が1.5という結果が得られた場合、その部署内で従業員の意見や感じ方に違いがあることを示唆しています。

標準偏差を使う場面として、例えば、次のようなケースが考えられます。部署間や職種間でエンゲージメントスコアの分布を比較する際、平均値が同じでもばらつきが異なる可能性があります。標準偏差を確認することで、スコアの一貫性や組織内の意見の均一性を評価できます。

他方で、標準誤差は標本平均のばらつき、すなわち推定の精度を表します。これは、標本平均が、母集団の真の平均値をどの程度正確に推定できているかを示しています。標準誤差が小さいほど、標本平均は母平均の良い推定値となります。

標準誤差を使う主な場面は、統計的推測を行う際です。例えば、エンゲージメントスコアの信頼区間を計算する場合や、部署間の平均値の差が統計的に有意かどうかを検定する場合に標準誤差を用います。必要なサンプルサイズを決定する際にも、標準誤差の大きさを考慮することが重要です。

エラーバーとの関係

エラーバーとは、グラフ上で数値のばらつきや不確実性を視覚的に表現する方法です。平均値を示す点や棒グラフに範囲を示すような線を引いて描かれます。エラーバーの長さは、データの特性や分析の目的に応じて、標準偏差または標準誤差を用いて設定されます。組織サーベイの結果をグラフ化する際、エラーバーを付けることで、より豊かな情報を提供することができます。

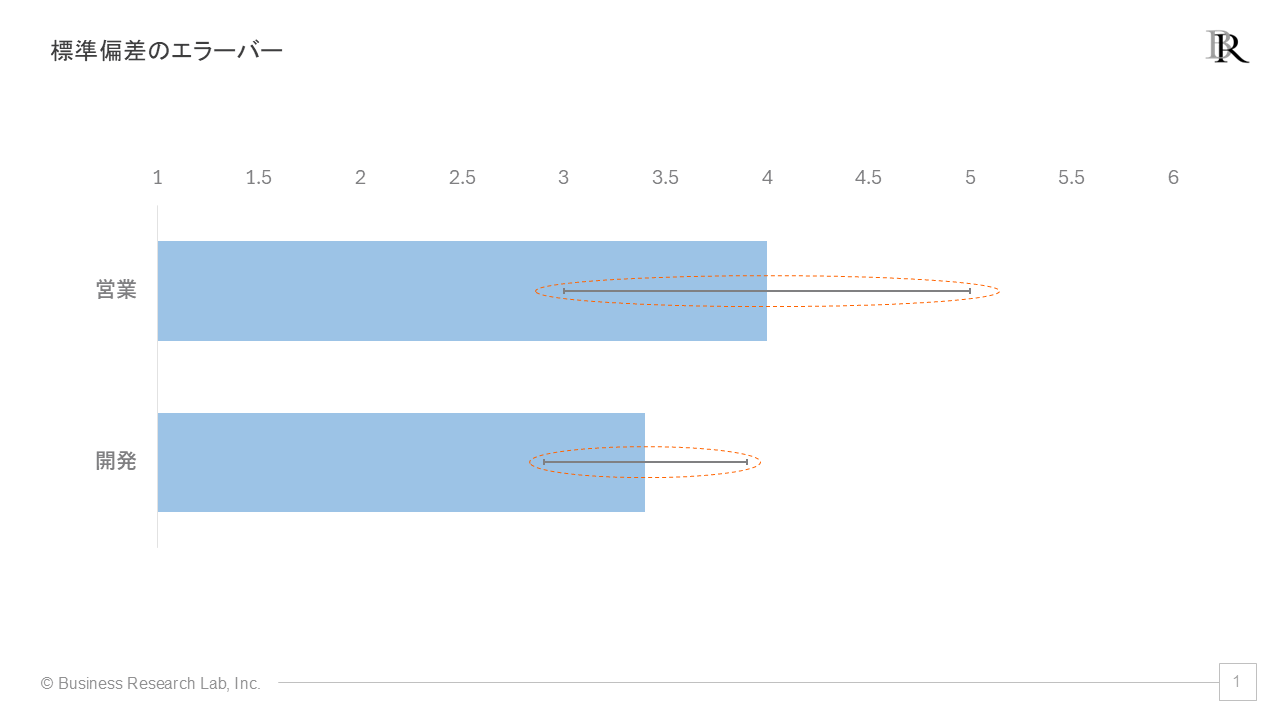
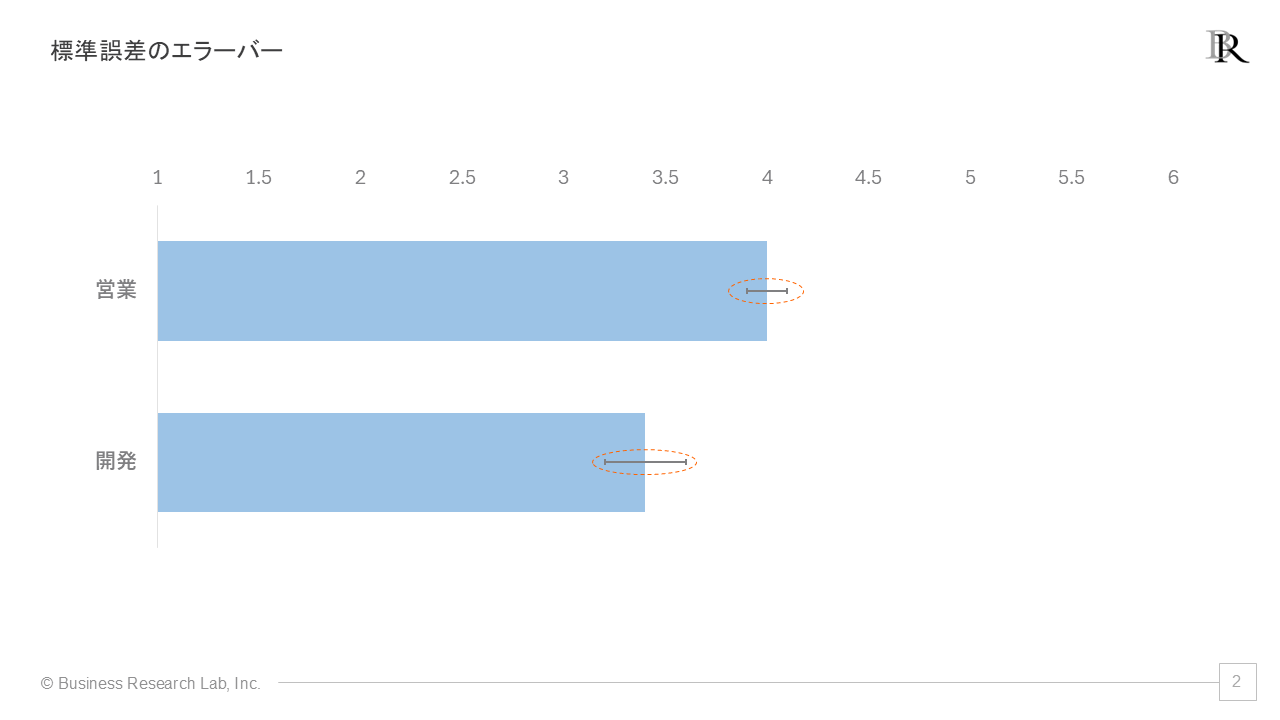
標準偏差を用いたエラーバーは、個々のデータのばらつきを視覚的に表現します。例えば、上のように部署ごとのエンゲージメントスコアを棒グラフで表示する際、各棒グラフに標準偏差のエラーバーを付けることで、回答のばらつきの大きさを直感的に理解できます。営業のように平均値が4.0で標準偏差が1.0の場合、エラーバーは左右に1.0単位の長さで描かれ、データの約68%がこの範囲に含まれることを示します。これによって、部署間でスコアの分布の違いを視覚的に比較することができます。

標準誤差を用いたエラーバーは、推定の精度を視覚的に表現します。例えば、複数の部署のエンゲージメントスコアを比較する際、各平均値に標準誤差のエラーバーを付けることで、推定の不確実性を示すことができます。

二つの部署のエラーバー（標準誤差を用いたもの）が重なっていない場合、それらの平均値の差は統計的に有意である可能性があります[5]。これは、標準誤差が示す推定の不確実性の範囲を考慮したときに、二つの平均値が異なる母集団から得られた可能性が高いことを意味します。例えば、標準誤差の2倍（約95%信頼区間に相当）のエラーバーを使用した場合、二つのエラーバーが重なっていなければ、その二つの平均値の差は統計的に有意である可能性があります。

ただし、この視覚的な判断による解釈は、あくまでも補助的なものとして扱う必要があります。エラーバーの重なりだけでは、データの分布の形状、サンプルサイズの違い、多重比較の問題など、統計的検定で考慮すべき多くの要因を完全には考慮できないからです。正確な統計的判断を行うためには、t検定や分散分析などの統計的検定を実施するほうが良いでしょう。エラーバーは、そのような詳細な分析の前段階として、データの全体像を把握し、注目すべき差異を見つけるためのツールとして活用できます。

また、サンプルサイズの違いがエラーバーの長さに与える影響についても注意が必要です。標準誤差はサンプルサイズの平方根に反比例するため、サンプルサイズが大きい部署ほどエラーバーは短くなります。例えば、同じ標本標準偏差（s=1.0）を持つ二つの部署があり、一方が400人（n₁=400）、他方が100人（n₂=100）からの回答だったとします。

• 部署1の標準誤差：SE₁=1.0/√400=0.05
• 部署2の標準誤差：SE₂=1.0/√100=0.10

このようにサンプルサイズの大きい部署1の方が標準誤差が小さく、それに応じてエラーバーも短くなります。より多くのデータに基づく推定の方が精度が高いことを反映しています。したがって、エラーバーの解釈の際には、サンプルサイズの違いも考慮に入れる必要があります。部署間でサンプルサイズが大きく異なる場合は、エラーバーの長さの違いがデータのばらつきの違いではなく、サンプルサイズの違いを反映している可能性があることに注意しましょう。

上の例では、標準偏差のエラーバーは営業の方が開発よりも長く、営業において得点がよりばらついていることがわかります。一方、標準誤差のエラーバーは営業の方が短く、母集団の平均をより高い精度で推定できていることを意味します。

脚注

[1] 本文で用いた身長の例は、母平均が既知である場合の説明ですが、母平均が未知である実際のサーベイデータの分析でも考え方は同じです。実際のサーベイでは母平均が未知ではありますが、母平均として何かしらの値が定まっていると考えて分析を進めます。つまり、母平均の値が具体的にいくつなのかは不明ですが、少なくとも「母集団において、平均値は決まっている」と見なしているわけです。このように、母平均が未知だとしても最終的に行きつく平均の値は決まっていると見なしていることから、母平均が既知の場合と同じ状況になるため、この場合でも、本当に「自由に変えられる」データの数は全体の数から1を引いた数になります。

[2] このような特徴を持つ統計量を「不偏推定量」と呼びます。

[3] リッカート尺度を用いたサーベイでは、天井効果（多くの回答が最高点に集中）や床効果（多くの回答が最低点に集中）が生じる可能性があります。このような場合、データの分布は正規分布から外れ、平均値や標準偏差の解釈が難しくなります。とりわけ、組織サーベイでは社会的望ましさによって高評価に偏りやすい概念に注意が必要です。

[4] 中心極限定理が成り立つためには、二つの条件があります。一つ目は、データが互いに独立であることです。これは、ある従業員の回答が他の従業員の回答に影響を与えないことを意味します。二つ目は、データの分散が有限であることです。つまり、極端な値が出現する確率が十分に小さいことが必要です。組織サーベイの場合、選択肢が限定されているため、この条件は自然に満たされるでしょう。これらの条件が満たされない場合、中心極限定理は成立せず、標準誤差の解釈が難しくなる可能性があります。

[5] エラーバーの重なりと統計的有意性の関係は直感的に理解しやすいため、本文では取り上げましたが、必ずしも一致するわけではないことに注意が必要です。例えば、2つのグループのエラーバーが少し重なっていても、t検定では有意な差が検出される場合があります。これは、t検定が2つのグループの分散や共分散を考慮しているためです。逆に、エラーバーが重なっていなくても、有意でない場合もあります。そのため、本文でも述べた通り、エラーバーは視覚的な参考情報として捉え、正確な統計的判断は適切な検定手法に基づいて行うことが重要です。

執筆者

伊達 洋駆　株式会社ビジネスリサーチラボ 代表取締役
神戸大学大学院経営学研究科 博士前期課程修了。修士（経営学）。2009年にLLPビジネスリサーチラボ、2011年に株式会社ビジネスリサーチラボを創業。以降、組織・人事領域を中心に、民間企業を対象にした調査・コンサルティング事業を展開。研究知と実践知の両方を活用した「アカデミックリサーチ」をコンセプトに、組織サーベイや人事データ分析のサービスを提供している。著書に『60分でわかる！心理的安全性 超入門』（技術評論社）や『現場でよくある課題への処方箋 人と組織の行動科学』（すばる舎）、『越境学習入門 組織を強くする「冒険人材」の育て方』（共著；日本能率協会マネジメントセンター）などがある。2022年に「日本の人事部 HRアワード2022」書籍部門 最優秀賞を受賞。東京大学大学院情報学環 特任研究員を兼務。